CHAPTER 16 PROJECT The Melting Arctic Ice Cap

In this project we study the changes in the thickness of sea ice that forms in the Arctic. There are many factors that affect the behavior of sea ice: abiotic factors such as, temperature, both that of the underlying water and air; wind, sea currents, and the motion of the Earth, and biotic factors such as plant and animal life. We examine only one factor: temperature.

We begin with a principle of thermodynamics: The direction of heat transfer is from a warmer to a cooler medium. Fourier's Law of Conduction states that the rate of heat flow \(\dfrac{dQ}{dt}\) through a homogeneous solid is directly proportional to the area \(A\) of the solid orthogonal to the direction of the heat flow, and to the change \(\Delta T\) in the temperature \(T\) and is inversely proportional to the thickness \(x\) of the solid. See Figure 8. The constant of proportionality \(k\) depends on the homogeneous solid and is called the thermal conductivity of the solid.

• 1. Write Fourier's Law of Conduction as a differential equation.
  
  A simple model depicting sea ice consists of a layer of air, a layer of sea ice, and a layer of sea water. A closer look at this model actually shows another layer directly below the ice. See Figure 9. It is this thin layer of super-cold, almost freezing water that is of interest in this project.
  
  
  

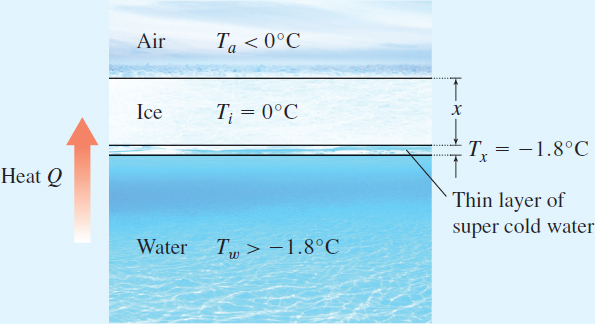  Figure 9 Model of sea ice
  
  In this model heat flows from the warmer water beneath the ice, through the ice, to the colder air above the ice.
• 2. Using \(k=2.1\, \rm{W/mK}\) (the thermal conductivity for sea ice), \(\ A=1\,\rm{m}^{2}\) as the surface area of the ice, \(x\,\rm{m}\) as the thickness of the ice, \(T_{\omega}=-1.8\,\rm{^{\circ}{\rm C}}\) as the near freezing temperature of the layer of sea water directly beneath the ice, and \(T_{a}=-20\, \rm{^{\circ}{\rm C}}\) as the (average winter) temperature of Arctic air, write Fourier's Law of Conduction.
  
  Then as the thin layer of sea water directly below the ice loses heat \(Q\), it begins to freeze. The amount of water that freezes satisfies the equation: \[ Q=334m \] where \(334\,\rm{J}/\rm{g}\) is the heat needed to freeze \(1\,\rm{g}\) of water, and \(m\) is the mass of the thin layer of water that freezes.
• 3. Find an expression for the mass \(m\) of the layer of water directly below the ice that freezes. (The mass density \(\rho \) of freezing sea water is \(1.025\,\rm{g}/\rm{ml}\)). Recall that the surface area of the ice is \(A=1\,\rm{m}^{2}\).
• 4. Find the rate of change in heat \(Q\) with respect to the thickness \(x\) of the ice.
• 5. Combine the result from Problem 4 with Fourier's Law of Conductivity (Problem 2) to find the rate of change in thickness of the ice with respect to time.
• 6. Solve the differential equation found in Problem 5. Then use the initial condition that at time \(t=0,\) the thickness of the ice is \(x=x_{0}.\)
• 7. Interpret the solution of the differential equation in Problem 6. Is the rate of change of the thickness of the ice increasing or decreasing over time?
• 8. Discuss whether this simple model offers a possible explanation for NASA's finding that the multi-year ice is melting faster than seasonal and other perennial ice.
• 9. Investigate some of the other factors that affect the behavior of sea ice and write a position paper on the impact of at least one these other factors on the depth of ice in the Arctic.

To read more and to see a how the Arctic Ice cap has changed from 1980–2012, visit http://www.nasa.gov/topics/earth/features/thick-melt.html