16.2 Assess Your UnderstandingPrinted Page 1070
Concepts and Vocabulary
The general solution of the differential equation dydx=xy is __________.
y=Ce0.5x2
True or False If f(tx,ty)=tkf(x,y), for all t>0, where k is a real number, then the function f is said to be homogeneous of degree k in x and y.
True
If F(x,y,C)=0 and G(x,y,K)=0 are one-parameter families of curves in which each member of one family intersects the members of the other family orthogonally, then the two families are said to be orthogonal __________ of each other.
Trajectories
If M(x,y)dx+N(x,y)dy=0 is a homogeneous differential equation, then it can be transformed into an equation whose variables are separable by using the substitution _________ , where _________ is a differentiable function of x.
y=xv(x); v=v(x)
Skill Building
In Problems 5–14, solve each differential equation.
dydx=xsecy
y=sin−1(12x2+C)
cosydydx=2x
dydx=ey−x
y=−ln(e−x+C)
xdydx+2y=5
dydx=cosxdydx−ysinx
y=C1−cosx
dydx=x+ydydx
dydx+xy=x
y=1−Ce−0.5x2
(3x+1)dx+ex+ydy=0
lnxdxdy=xy
y=C(√x)lnx where C≠0 is a constant.
dydx=x+22−y
In Problems 15–20, obtain a particular solution of each differential equation. (Use the results obtained for Problems 5–10.
dydx=xsecy,y=π4 when x=1
y=sin−1(12x2+√2−12)
cosydydx=2x,y=π3, when x=−1
dydx=ey−x;y=0 when x=0
y=x
xdydx+2y=5;y=1 when x=−1
dydx=cosxdydx−ysinx;y=12 when x=π
y=11−cosx
dydx=x+ydydx,y=1 when x=2
In Problems 21–30, determine if each function is homogeneous. If it is, find its degree.
f(x,y)=2x2−3xy−y2
Function f is a homogeneous function of degree 2.
f(x,y)=x3−xy2+y3
f(x,y)=x3−xy+y3
Function f is not a homogeneous function.
f(x,y)=x2−xy2+y2
f(x,y)=2x+√x2+y2
Function f is a homogeneous function of degree 1.
f(x,y)=√x+y
f(x,y)=tan(3xy)
Function f is a homogeneous function of degree 0.
f(x,y)=ex/y
f(x,y)=lnxy
Function f is a homogeneous function of degree 0.
f(x,y)=xlnx−xlny
In Problems 31–42, solve each homogeneous differential equation. Follow the steps on p. 1064.
(x−y)dx+xdy=0
y=Cx−xln|x|
(x+y)dx+xdy=0
(x2+y2)dx+(x2−xy)dy=0
yx−2ln|x+y|+ln|x|+C=0
xydx+(x2+y2)dy=0
dydx=y−xy+x
12ln(x2+y2)+tan−1(yx)=C
dydx=x+2y2x+y
xdydx=x+y
y=x(C+ln|x|)
x(x2−y2)dydx−y(x2+y2)=0
dydx=2xyx2+y2
y2−x2y=C
dydx=x+2y2x−y
x2dydx=x2+xy−4y2; y=1 when x=−1
x4(2y−x)2y+x=3
x(x2−y2)dydx−y(x2+y2)=0;y=−2 when x=−1
In Problems 43–46, find the orthogonal trajectories of each family of curves. Graph the members of each family that contain the point (2,1).
xy=C
The orthogonal trajectories for the family xy=C is the family y2=x2+K. The graph of xy=2 and y2=x2−3 is shown.

y2=2(C−x)
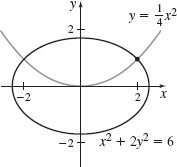
y=Cx2
The orthogonal trajectories for the family y=Cx2 is the family x2+2y2=K. The graph of y=14x2 and x2+2y2=6 is shown.
x2=Cy3
1071
Applications and Extensions
In Problems 47 and 48, solve each differential equation by letting x=u+h and y=v+k, where h and k are constants chosen so as to eliminate the constant terms on the right side.
dydx=y−x−3y+x+4
12ln((2y+1)2+(2x+7)2)+tan−1(2y+12x+7)=C
dydx=x+2y−32x−y+1;y=4 when x=3
Orthogonal Families Find the orthogonal trajectories of the family of parabolas y2=4Cx.
2x2+y2=K
Orthogonal Trajectories Find the orthogonal trajectories of all circles tangent to the x-axis at (3,0).
Newton's Law of Heating Newton's Law of Heating states that the rate of increase of the temperature u of an object immersed in a medium of constant temperature T is proportional to the difference T−u. The differential equation that models the temperature of the object at time t is dudt=k(T−u)
where k is a positive constant.
- (a) Find a solution of this differential equation.
- (b) Find the particular solution that satisfies the initial condition u(0)=u0.
- (c) A metal bar with initial temperature 25∘C is dropped into a container of boiling water (100∘C). After 5 seconds, the temperature of the bar is 35∘C. What will the temperature of the bar be after 1 min?
- (d)
 Graph the particular solution to the differential equation found in (c).
Graph the particular solution to the differential equation found in (c). - (e) Use the graph to approximate how long will it take for the temperature of the bar to be within 0.5∘C of the temperature of the boiling water.
- (a) u=T−C⋅e−kt
- (b) u=T−(T−u0)e−kt
- (c) After 1 minute, the temperature of the bar is 86.533∘C.
- (d) The graph of the particular solution to the differential equation is shown.
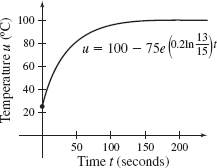
- (e) The temperature of the bar will be within 0.5∘C of the temperature of the boiling water after approximately 175.1 seconds, or about 3 minutes.
Newton's Law of Cooling According to Newton's Law of Cooling, the rate at which a body cools is proportional to the difference between the temperature of the body and the temperature of the surrounding medium. A certain steel bar has a temperature of 1230∘C and cools to 1030∘C in 10 min when the surrounding temperature is 30∘C.
- (a) How long will it take for the bar to cool to 80∘C?
- (b)
 Graph the temperature of the steel bar over the interval t=0 to t=240 (i.e., for the first 4 h).
Graph the temperature of the steel bar over the interval t=0 to t=240 (i.e., for the first 4 h). - (c) Use the graph to approximate when the steel bar cools to 50∘C.
Sales Growth The annual sales of a new company are expected to grow at a rate that is proportional to the difference between the sales and an upper limit of $20 million. Sales are $0 initially and are $3 million for the second year.
- (a) Determine the annual sales at any time t.
- (b) According to the model, what will sales be during the eighth year of operations?
- (c) How long will it take for sales to reach $12 million?
- (d)
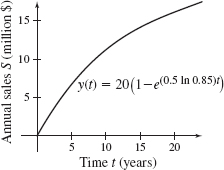
 Graph the annual sales of the company for its first 20 years of operation.
Graph the annual sales of the company for its first 20 years of operation.
- (a) y(t)=20(1−e(0.5ln0.85)t)
- (b) During the eighth year of operation, the sales will be approximately 9.56 million dollars.
- (c) Sales will reach $12 million dollars in approximately 11.28 years.
- (d) The graph of the annual sales of the company for its first 20 years of operation is shown.
Bacteria Growth A culture of bacteria is growing in a medium that can support a maximum of 1,000,000 bacteria. The rate of growth of the population at time t is proportional to the difference between 1,000,000 and the number present at time t. The culture contains 1000 bacteria initially, and after 1 h there are 1500 bacteria.
- (a) How many bacteria will there be after 5 h?
- (b) When will the culture contain 9950 bacteria?
Learning Curve The number of words per minute W that a person can text increases with practice. Assume that the rate of change of W is proportional to the difference between an upper limit of 150 words per minute and W. That is, the rate of change is proportional to 150−W. Suppose a beginner cannot text at all, that is, W=0 when t=0, and can text 30 words per minute after 10 h of practice.
- (a) How many words per minute can he text after 25 h of practice?
- (b) How many hours of practice will be required in order for him to text 100 words per minute?
- (c)
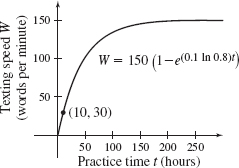
 Graph the number of words per minute W a beginner can text as a function of hours of practice.
Graph the number of words per minute W a beginner can text as a function of hours of practice.
- (a) After 25 hours of practice, the person can text approximately 64.1 words per minute.
- (b) The person will need approximately 49.2 hours of practice in order to text 100 words per minute.
- (c) The graph of texting speed as a function of hours of practice is shown.
Drug Concentration A drug is injected into a patient's bloodstream at a constant rate of r mg/s. Simultaneously, the drug is removed from the bloodstream at a rate proportional to the amount y(t) present at time t.
- (a) Find a differential equation that models this problem.
- (b) Find a solution of the differential equation in (a).
- (c) Find the particular solution that satisfies the initial condition y(0)=0.
Friction The frictional force f on an object sliding over a surface depends on the speed v of the object and can be modeled by the function f=−Av, where A is a positive constant that depends on the two surfaces. Note:The force is negative because the direction of the friction is opposite to the direction of the velocity.
- (a) Express the frictional force f as a differential equation by using Newton's Second Law, F=ma.
- (b) Solve the differential equation found in (a) for v(t). Assume the object slides over the surface with an initial speed v0.
- (c) Suppose that the frictional force on a 25-kg sled is 150N when the speed of the sled is 10 m/s. Determine the value of the constant A.
- (d) How long will it take the sled to slow down to 10% of its initial speed?
- (e) How far will the sled travel while slowing down to 1.0 m/s ? Assume an initial speed of 10 m/s.
- (a) dvdt=−Amv
- (b) v=v0e−Amt
- (c) A = 15 kg/s
- (d) The sled will slow down to 10% of its initial speed in approximately 3.84 seconds.
- (e) While slowing down to 1.0 m/s, the sled will travel 15 meters.
Friction The frictional force f on an object sliding over a surface depends on the speed v of the object and can be modeled by the function f=−B√v, where B is a positive constant that depends on the two surfaces. Note: The force is negative because the direction of the friction is opposite to the direction of the velocity.
- (a) Express the frictional force f as a differential equation by using Newton's Second Law, F=ma.
- (b) Solve the differential equation found in (a) for v(t). Assume the object slides over the surface with an initial speed v0.
- (c) Suppose that the frictional force on a 25-kg sled is 150N when the speed of the sled is 10 m/s. Determine the value of the constant B.
- (d) How long will it take the sled to slow down to 10% of its initial speed?
- (e) How far will the sled travel while slowing down to 1.0 m/s? Assume an initial speed of 10 m/s.
1072
Electronics: Discharging a Capacitor In a circuit, a capacitor C carries an initial charge q0 and discharges through a resistor R. Using Kirchhoff's rules with this circuit, we obtain the differential equation dqdt+qRC=0
where q is the charge, in Coulombs, on the capacitor at any time t, and R and C are constants.
- (a) Solve the differential equation for the charge q as a function of time t.
- (b) In a typical laboratory circuit, R=150 Ω (ohms) and C=5.0 µF (microfarads). How long will it take the discharging capacitor to lose 99% of its initial charge?
[Hint: The product (1Ω) (1F) = 1 second.]
- (a) q=q0⋅e−1RCt
- (b) The discharging capacitor will lose 99% of its initial charge in approximately 0.00345 seconds.
Air Resistance At high speeds, air resistance (drag) can be modeled by Fdrag=−Av2, where A is a positive constant that depends on the shape of the object, its surface texture, and the conditions of the air. Note: The force is negative because the direction of the drag is opposite to the direction of the velocity. Suppose, in a test facility, a projectile of mass m is launched with initial horizontal speed v0 on a frictionless horizontal track. The only force opposing the motion of the projectile is the drag.
- (a) Express the drag Fdrag as a differential equation by using Newton's Second Law, F=ma.
- (b) Solve the differential equation found in (a) for v(t).
- (c) What happens to the speed of the projectile as t becomes arbitrarily large?
Challenge Problems
Orthogonal Families Find the orthogonal trajectories of the family of hyperbolas x2C2−y24−C2=1, where 0<C<2.
y=Kx−C24−C2
Orthogonal Trajectories Find the orthogonal trajectories of the family of parabolas with a common vertex at (1,2) having a vertical axis. Graph the member of each family that contains the point (2,3).
Velocity of a Projectile Near Earth's surface the attraction due to gravity is practically constant, but according to Newton's law, the force of attraction exerted by Earth on a given body is kx2, where x is the distance of the body from the center of the Earth.
- (a) Show that if a projectile is shot upward from Earth's surface with initial velocity v0, and if air resistance is neglected, then v2=v20−2Rg+2R2gx where R=3960 mi is the radius of Earth and g is the acceleration due to gravity. Hint: d2xdt2=dvdt=dvdxdxdt=vdvdx
- (b) Find the smallest value of v0 necessary to keep the projectile going indefinitely (neglecting the attractive forces due to celestial bodies other than Earth). This is called the escape velocity for Earth.
- (a) See Student Solutions Manual.
- (b) v0=√2Rg
Rate of Flow From physics, it is known that the rate of flow of water from a tank through an orifice of area A square feet is approximately dVdt=−kA√2gh, where k=0.6, g=32 ft/s2, and h is the height of the water level, in feet, above the orifice. Suppose a cylindrical tank with height 6 ft and diameter 3 ft is filled with water. At time t=0, a valve in the bottom of the tank is opened and the water begins draining through a circular hole of diameter 1 in.
- (a) Express the height of the water in the tank as a function of time t.
- (b) How much time is required to empty the tank?
Rate of Flow If the water in a tank leaks out through a small hole in the bottom, then the rate of flow is proportional to the square root of the height of the water in the tank. Prove that if the tank is a cylinder with a vertical axis, then the time required for three-fourths of the water to leak out is equal to the time required for the remaining one-fourth of the water to leak out.
See Student Solutions Manual.
Water Level A cylindrical tank has a leak in the bottom, and water flows out at a rate proportional to the pressure at the bottom. If the tank loses 2% of its water in 24 h, when will it be half empty?
