Question

True or False The differential equation \(xy\,dx+\dfrac{ x^{2}}{2}dy=0\) is exact.

Question

True or False The differential equation \(y\cos x\,dx-\sin x\,dy=0\) is exact.

Question

True or False If \(\dfrac{\partial M}{\partial x}= \dfrac{\partial N}{\partial y},\) then \(M(x,y)\,dx+ N(x,y)\,dy=0\) is an exact differential equation.

Question

If the differential equation \(M(x,y)\,dx+N(x,y)\,dy=0\) is not exact, but \(a( x,y) M(x,y)\,dx+a( x,y) N(x,y)\,dy=0\) is an exact differential equation, then the expression \(a( x,y) \) is called a(n) _____ _____.

Question

\((4x-2y+5)\,dx+(2y-2x)\,dy=0\)

Question

\((3x^{2}+3xy^{2})\,dx+(3x^{2}y-3y^{2}+2y)\,dy=0\)

Question

\((a^{2}-2xy-y^{2})\,dx-(x+y)^{2}dy=0\), \(a\) is constant

Question

\((2ax+by+g)\,dx+(2e^{y}+bx+h)\,dy=0\), \(a\), \(b\), \(g\), \(h\) are constants

Question

\(\dfrac{1}{y}\,dx-\dfrac{x}{y^{2}}\,dy=0\)

Question

\(\dfrac{y\,dx-x\,dy}{x^{2}}=0\)

Question

\((x-1)^{-1}y\,dx+ [ \ln (2x-2)+y^{-1}]\,dy=0\)

Question

\(2xy^{-1}dy+(2\;\ln (5y)+x^{-1})\,dx=0\)

Question

\((x+3)^{-1}\cos y\,dx-[\sin y\ln (5x+15)-y-1]\,dy=0\)

Question

\(p^{2}\sec ( 2\theta ) \tan ( 2\theta )\,d\theta +p [ \sec ( 2\theta ) +2]\,dp=0\)

Question

\(\cos (x+y^{2})\,dx+2y\cos (x+y^{2})\,dy=0\)

Question

\([ \sin ( 2\theta ) -2p\cos ( 2\theta ) ]\,dp+ [ 2p\cos ( 2\theta ) +2p^{2}\sin ( 2\theta ) ]\,d\theta =0\)

Question

\(e^{2x}(dy+2y\,dx)=x^{2}dx\)

Question

\(e^{x^{2}}(dy+2xy\,dx)=3x^{2}dx\)

Question

\(\left[ \dfrac{1}{x+y}+y^{2}\right]\;dx+\left[ \dfrac{1}{x+y} +2xy\right]\;dy=0\)

Question

\(\dfrac{y^{2}-2x^{2}}{xy^{2}-x^{3}}\,dx+ \dfrac{2y^{2}-x^{2}}{y^{3}-x^{2}y}\,dy=0\)

Question

\(2y^{3}\sin ( 2x)\,dx-3y^{2}\cos ( 2x)\,dy=0\)

Question

\(\dfrac{3y^{2}}{x^{2}+3x}\,dx+\left( 2y\ln \dfrac{5x}{x+3}+3\sin y\right)\;dy=0\)

Question

\((1+y^{2}+xy^{2})\,dx+(x^{2}y+y+2xy)\,dy=0\); \(y(1)=1\)

Question

\((3x^{2}y^{-1}+2x)\,dx+(y^{2}-x^{3}y^{-2})\,dy=0\); \(y(3)=3\)

Question

\((2xy-\sin x)\,dx=(2y-x^{2})\,dy\); \(y(0)=1\)

Question

\(y[y+\sin x]\,dx-\left[ \cos x-2xy+\dfrac{1}{1+y^{2}}\right]\;dy=0\); \(y(0)=1\)

Question

Integrating Factors Suppose the equation \(M(x,y)\,dx+N(x,y)\,dy=0\) has the property that \(\dfrac{\dfrac{\partial N}{\partial x}-\dfrac{\partial M}{\partial y}}{M }\) is a function of \(y\) only. If \[\begin{equation*} u(y)=e^{\Big[ \int \frac{\frac{\partial N}{\partial x}-\frac{\partial M}{ \partial y}}{M}\,dy\Big] }=\exp \left[ \int \frac{\dfrac{\partial N}{ \partial x}-\dfrac{\partial M}{\partial y}}{M}\,dy\right] \end{equation*}\]

show that \(u(y)\left[ M(x,y)\,dx+N(x,y)\,dy\right] =0\) is an exact differential equation.

Question

Integrating Factors Suppose the equation \(M(x,y)\,dx+N(x,y)\,dy=0\) has the property that \(\dfrac{\dfrac{\partial M}{\partial y}-\dfrac{\partial N}{\partial x}}{N }\) is a function of \(x\) only. If \[\begin{equation*} u(x)=e^{\Big[ \int \frac{\frac{\partial M}{\partial y}-\frac{\partial N}{ \partial x}}{N}\,dx\Big] }=\exp \left[ \int \frac{\dfrac{\partial M}{\partial y}-\dfrac{\partial N}{ \partial x}}{N}\,dx\right] \end{equation*}\]

show that \(u(x)[M(x,y)\,dx+N(x,y)\,dy]=0\) is an exact differential equation.

Question

\(( 4x^{2}+y^{2}+1)\,dx+(x^{2}-2xy)\,dy=0\)

Question

\(4x^{2}y\,dx+(x^{3}+y)\,dy=0\)

Question

\(y\,dx+(x^{2}y-x)\,dy=0\)

Question

\((\cos y+x)\,dx+x\sin ydy=0\)

Question

\((x^{2}-x\sin y)\,dx+x^{2}\cos y\,dy=0\)

Question

Measuring the Effect of Pollution A crash in the Gulf of Mexico resulted in an oil spill at the point \(A\) shown in the figure below. Several months after the spill, measurements are taken to determine whether the oil is still affecting the marine environment of the Gulf. The contour curves shown in the figure are curves of constant oil concentration. These curves are modeled by the differential equation \[\begin{equation*} \dfrac{2\dfrac{\beta -y}{100}-2\cos \dfrac{\beta -y}{100}}{2\dfrac{\alpha -x }{100}+4\cos \dfrac{\alpha -x}{100}^{{}}}y^{\prime} ( x) =1 \end{equation*}\]

where \(\alpha\) and \(\beta\) are specified constants.

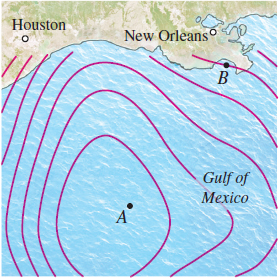
1. Find the solution of the differential equation.
2. The solution from (b) can be interpreted as the oil concentration in pounds of oil per million gallons at a point \(( x,y)\). Suppose the point \(A\) is at the origin and the point \(B\) is \((162.14,250.64)\). Use the initial condition \(f(0,0) =1247.2\) to find the oil concentration at \(B,\) given \(\alpha =93.43\) and \(\beta =59.12.\)