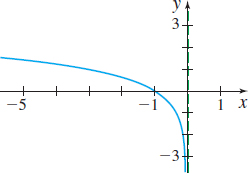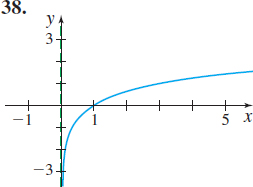P.5 Assess Your UnderstandingPrinted Page 48
Concepts and Vocabulary
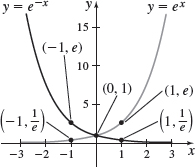
The graph of every exponential function f(x)=ax, a>0 and a≠1, passes through three points: _____, _____, and _____.
(−1,1a), (0,1), (1,a)
True or False The graph of the exponential function f(x)=(32)x is decreasing.
False
If 3x=34, then x= _____.
4
If 4x=82 then x= _____.
3
True or False The graphs of y=3x and y=(13)x are symmetric with respect to the line y=x.
False
True or False The range of the exponential function f(x)=ax, a>0 and a≠1, is the set of all real numbers.
False
The number e is defined as the base of the exponential function f whose tangent line to the graph of f at the point (0,1) has slope _____.
1
The domain of the logarithmic function f(x)=logax is _____.
{x|x>0}
The graph of every logarithmic function f(x)=logax, a>0 and a≠1, passes through three points: _____, _____, and _____.
(1a,−1), (1,0), (a,1)
Multiple Choice The graph of f(x)=log2x is [(a) increasing, (b) decreasing, (c) neither].
(a)
True or False If y=logax, then y=ax.
False
True or False The graph of f(x)=logax, a>0 and a≠1, has an x-intercept equal to 1 and no y -intercept.
True
True or False lnex=x for all real numbers.
True
lne= _____.
1
Explain what the number e is.
Answers will vary.
What is the x-intercept of the function h(x)=ln(x+1)?
0
Practice Problems
Suppose that g(x)=4x+2.
- (a) What is g(−1)? What is the corresponding point on the graph of g?
- (b) If g(x)=66, what is x? What is the corresponding point on the graph of g?
- (a) g(−1)=94, (−1,94)
- (b) x=3, (3,66)
Suppose that g(x)=5x−3.
- (a) What is g(−1)? What is the corresponding point on the graph of g?
- (b) If g(x)=122, what is x? What is the corresponding point on the graph of g?
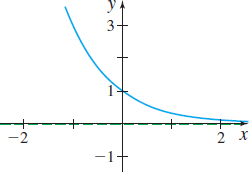
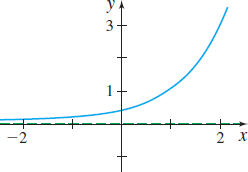
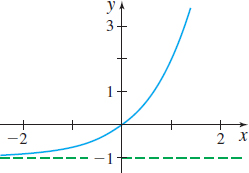
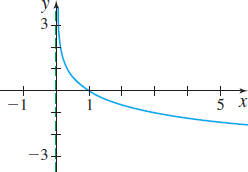
In Problems 19–24, the graph of an exponential function is given. Match each graph to one of the following functions:
- (a) y=3−x
- (b) y=−3x
- (c) y=−3−x
- (d) y=3x−1
- (e) y=3x−1
- (f) y=1−3x
(a)
(c)
(b)
In Problems 25–30, use transformations to graph each function. Find the domain and range.
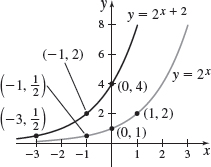
f(x)=2x+2
Domain: (−∞,∞), range: (0,∞)
f(x)=1−2−x/3
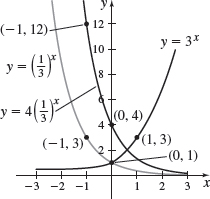
f(x)=4(13)x
Domain: (−∞,∞), range: (0,∞)
f(x)=(12)−x+1
f(x)=e−x
Domain: (−∞,∞), range: (0,∞)
f(x)=5−ex
49
In Problems 31–34, find the domain of each function.
F(x)=log2x2
{x|x≠0}
g(x)=8+5ln(2x+3)
f(x)=ln(x−1)
{x|x>1}
g(x)=√lnx
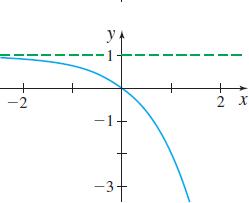
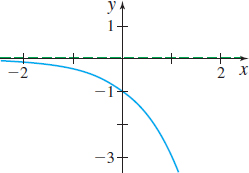
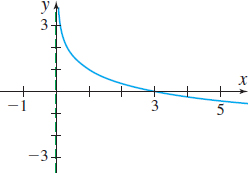
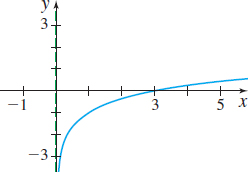
In Problems 35–40, the graph of a logarithmic function is given. Match each graph to one of the following functions:
- (a) y=log3x
- (b) y=log3(−x)
- (c) y=−log3x
- (d) y=log3x−1
- (e) y=log3(x−1)
- (f) y=1−log3x
(b)
(f)
(c)
In Problems 41–44, use the given function f to:
- (a) Find the domain of f.
- (b) Graph f.
- (c) From the graph of f, determine the range of f.
- (d) Find f−1, the inverse of f.
- (e) Use f−1 to find the range of f.
- (f) Graph f−1.
f(x)=ln(x+4)
- (a) a{x|x>−4}
- (b) (bandf)
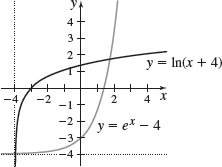
- (c) c(−∞,∞)
- (d) df−1(x)=ex−4
- (e) e(−∞,∞)
f(x)=12log(2x)
f(x)=3ex+2
- (a) a(−∞,∞)
- (b) (bandf)
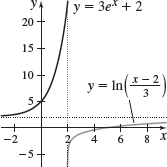
- (c) c{y|y>2}
- (d) df−1(x)=ln(x−23)
- (e) e{y|y>2}
f(x)=2x/3+4
How does the transformation y=ln(x+c), c>0, affect the x-intercept of the graph of the function f(x)=lnx?
It shifts the x-intercept c units to the left.
How does the transformation y=ecx, c>0, affect the y-intercept of the graph of the function f(x)=ex?
In Problems 47–62, solve each equation.
3x2=9x
x=0, x=2
5x2+8=1252x
e3x=e2ex
x=12
e4x⋅ex2=e12
e1−2x=4
x=1−ln42
e1−x=5
5(23x)=9
x=ln(95)3ln2
0.3(40.2x)=0.2
31−2x=4x
x=ln3ln36
2x+1=51−2x
log2(2x+1)=3
x=72
log3(3x−2)=2
logx(18)=3
x=12
logx64=−3
ln(2x+3)=2ln3
x=3
12log3x=2log32
![]() In Problems 63–66, use graphing technology to solve each equation. Express your answer rounded to three decimal places.
In Problems 63–66, use graphing technology to solve each equation. Express your answer rounded to three decimal places.
log5(x+1)−log4(x−2)=1
x≈2.787
lnx=x
ex+lnx=4
x≈1.315
ex=x2

- (a) If f(x)=ln(x+4) and g(x)=ln(3x+1), graph f and g on the same set of axes.
- (b) Find the point(s) of intersection of the graphs of f and g by solving f(x)=g(x) . Label any intersection points on the graph drawn in (a).
- (c) Based on the graph, solve f(x)>g(x).
- (a)
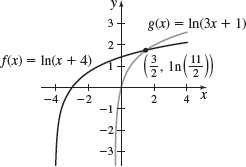
- (b) (32,ln112)
- (c) {x|−13<x<32}

- (a) If f(x)=3x+1 and g(x)=2x+2, graph f and g on the same set of axes.
- (b) Find the point(s) of intersection of the graphs of f and g by solving f(x)=g(x). Round answers to three decimal places. Label any intersection points on the graph drawn in (a).
- (c) Based on the graph, solve f(x)>g(x).