P.6 Assess Your UnderstandingPrinted Page 56
Concepts and Vocabulary
The sine, cosine, cosecant, and secant functions have period _____; the tangent and cotangent functions have period _____.
2π, π
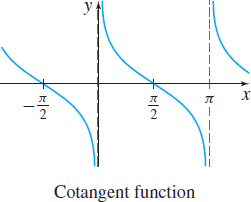
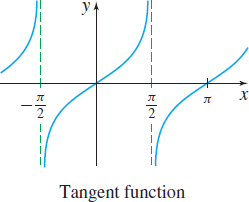
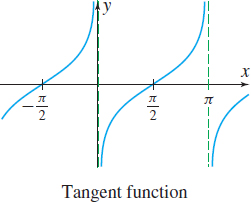
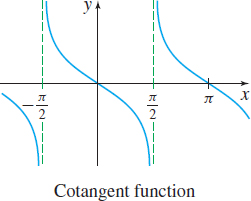
The domain of the tangent function f(x)=tanx is _____.
All real numbers except odd multiples of π2
The range of the sine function f(x)=sinx is _____.
{y|−1≤y≤1}
Explain why tan(π4+2π)=tanπ4.
The period of tanx is π.
True or False The range of the secant function is the set of all positive real numbers.
False
The function f(x)=3cos(6x) has amplitude _____ and period _____.
3, π3
True or False The graphs of y=sinx and y=cosx are identical except for a horizontal shift.
True
True or False The amplitude of the function f(x)=2sin(πx) is 2 and its period is π2.
False
True or False The graph of the sine function has infinitely many x-intercepts.
True
The graph of y=tanx is symmetric with respect to the _____.
Origin
The graph of y=secx is symmetric with respect to the _____.
y-axis
Explain, in your own words, what it means for a function to be periodic.
Answers will vary.
Practice Problems
In Problems 13–16, use the even-odd properties to find the exact value of each expression.
tan(−π4)
−1
sin(−3π2)
csc(−π3)
−2√33
cos(−π6)
57
In Problems 17–20, if necessary, refer to a graph to answer each question.
What is the y-intercept of f(x)=tanx?
0
Find the x-intercepts of f(x)=sinx on the interval [−2π,2π].
What is the smallest value of f(x)=cosx?
−1
For what numbers x, −2π≤x≤2π, does sinx=1? Where in the interval [−2π,2π] does sinx=−1?
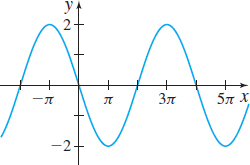
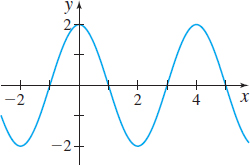
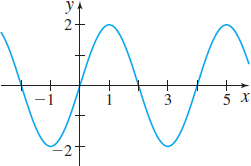
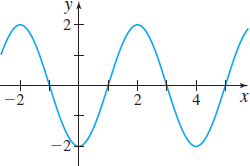
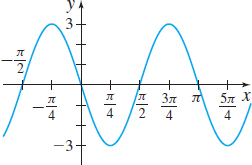
In Problems 21–26, the graphs of six trigonometric functions are given. Match each graph to one of the following functions:
- (a) y=2sin(π2x)
- (b) y=2cos(π2x)
- (c) y=3cos(2x)
- (d) y=−3sin(2x)
- (e) y=−2cos(π2x)
- (f) y=−2sin(12x)
(f)
(a)
(d)
In Problems 27–32, graph each function using transformations. Be sure to label key points and show at least two periods.
f(x)=4sin(πx)
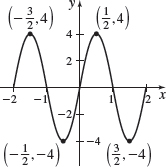
f(x)=−3cosx
f(x)=3cos(2x)−4
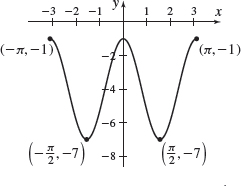
f(x)=4sin(2x)+2
f(x)=tan(π2x)
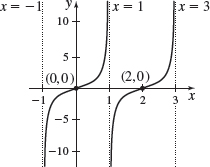
f(x)=4sec(12x)
In Problems 33–36, determine the amplitude and period of each function.
g(x)=12cos(πx)
12, 2
f(x)=sin(2x)
g(x)=3sinx
3, 2π
f(x)=−2cos(32x)
In Problems 37 and 38, write the sine function that has the given properties.
Amplitude: 2, Period: π
f(x)=2sin(2x)
Amplitude: 13, Period: 2
In Problems 39 and 40, write the cosine function that has the given properties.
Amplitude: 12, Period: π
f(x)=12cos(2x)
Amplitude: 3, Period: 4π
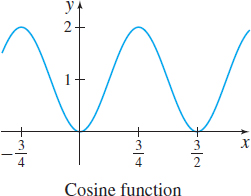
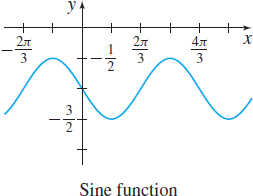
In Problems 41–48, for each graph, find an equation involving the indicated trigonometric function.
f(x)=−sin(32x)
f(x)=1−cos(4π3x)
f(x)=cotx
f(x)=tan(x−π2)