P.7 Assess Your UnderstandingPrinted Page 56
Concepts and Vocabulary
y=sin−1x if and only if x= _____, where −1≤x≤1 and −π2≤y≤π2.
siny
True or False sin−1(sinx)=x, where −1≤x ≤1.
False
True or False The domain of y=sin−1x is −π2≤x≤π2.
False
True or False sin(sin−10)=0.
True
True or False y=tan−1x means x=tany, where −∞<x<∞ and −π2≤y≤π2.
False
True or False The domain of the inverse tangent function is the set of all real numbers.
True
True or False sec−10.5 is not defined.
True
True or False Trigonometric equations can have multiple solutions.
True
Practice Problems
In Problems 9–20, find the exact value of each expression.
sin−1(√22)
π4
sin−1(−12)
sec−12
π3
tan−1√3
tan−1(−1)
−π4
sec−12√33
tan−1(tanπ4)
π4
tan−1(sin0)
sin(sin−135)
35
tan[sec−1(−3)]
sin−1(sin4π5)
π5
sec(sec−13)
Write cos(sin−1u) as an algebraic expression containing u, where |u|≤1.
√1−u2
Write tan(sin−1u) as an algebraic expression containing u, where |u|≤1.
Write sec(tan−1u) as an algebraic expression containing u.
√1+u2
Show that y=sin−1x is an odd function. That is, show sin−1(−x)=−sin−1x.
Show that y=tan−1x is an odd function. That is, show tan−1(−x)=−tan−1x.
See Student Solutions Manual.
Given that x=sin−112, find cosx, tanx, cotx, secx, and cscx.
In Problems 27–44, solve each equation on the interval 0≤θ<2π.
tanθ=−√33
{5π6,11π6}
sec3θ2=−2
64
2sinθ+3=2
{7π6,11π6}
1−cosθ=12
sin(3θ)=−1
{π2,7π6,11π6}
cos(2θ)=12
4cos2θ=1
{π3,2π3,4π3,5π3}
2sin2θ−1=0
2sin2θ−5sinθ+3=0
{π2}
2cos2θ−7cosθ−4=0
1+sinθ=2cos2θ
{π6,5π6,3π2}
sec2θ+tanθ=0
sinθ+cosθ=0
{3π4,7π4}
tanθ=cotθ
cos(2θ)+6sin2θ=4
{π3,2π3,4π3,5π3}
cos(2θ)=cosθ
sin(2θ)+sin(4θ)=0
{0,π3,π2,2π3,π,4π3,3π2,5π3}
cos(4θ)−cos(6θ)=0
In Problems 45–48, use a calculator to solve each equation on the interval 0≤θ<2π. Round answers to three decimal places.
tanθ=5
{1.373,4.515}
cosθ=0.6
2+3sinθ=0
{3.871,5.553}
4+secθ=0
- (a) On the same set of axes, graph f(x)=3sin(2x)+2 and g(x)=72 on the interval [0,π].
- (b) Solve f(x)=g(x) on the interval [0,π], and label the points of intersection on the graph drawn in (a).
- (c) Shade the region bounded by f(x)=3sin(2x)+2 and g(x)=72 between the points found in (b) on the graph drawn in (a).
- (d) Solve f(x)>g(x) on the interval [0,π].
- (a) (aandc)
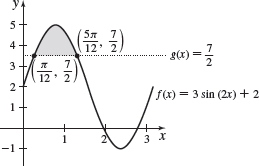
- (b) (π12,72), (5π12,72)
- (c) See (a).
- (d) {x|π12<x<5π12}
- (a) On the same set of axes, graph f(x)=−4cosx and g(x)=2cosx+3 on the interval [0,2π].
- (b) Solve f(x)=g(x) on the interval [0,2π], and label the points of intersection on the graph drawn in (a).
- (c) Shade the region bounded by f(x)=−4cosx and g(x)=2cosx+3 between the points found in (b) on the graph drawn in (a).
- (d) Solve f(x)>g(x) on the interval [0,2π].
