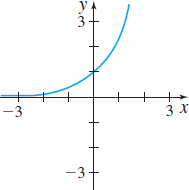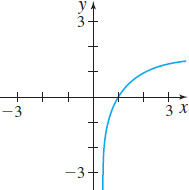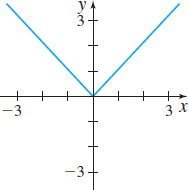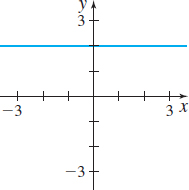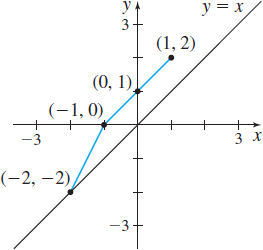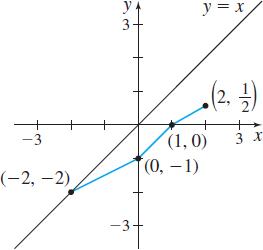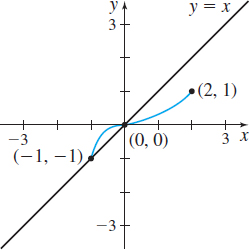Loading [MathJax]/jax/output/CommonHTML/jax.js

P.4 Assess Your Understanding

Printed Page 37

Concepts and Vocabulary

  1. True or False  If every vertical line intersects the graph of a function f at no more than one point, f is a one-to-one function.

False

  1. If the domain of a one-to-one function f is [4,∞), the range of its inverse function f−1 is _____.

[4,∞)

  1. True or False  If f and g are inverse functions, the domain of f is the same as the domain of g.

False

  1. True or False  If f and g are inverse functions, their graphs are symmetric with respect to the line y=x.

True

  1. True or False  If f and g are inverse functions, then (f∘g)(x)=f(x)⋅g(x).

False

  1. True or False  If a function f is one-to-one, then f(f−1(x))=x, where x is in the domain of f.

False

  1. Given a collection of points (x,y), explain how you would determine if it represents a one-to-one function y=f(x).

Answers will vary.

  1. Given the graph of a one-to-one function y=f(x), explain how you would graph the inverse function f−1.

Answers will vary.

Practice Problems

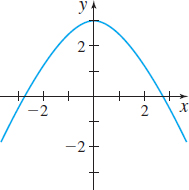
In Problems 9–14, the graph of a function f is given. Use the Horizontal-line Test to determine whether f is one-to one.

One-to-one

Not one-to-one

One-to-one

In Problems 15–18, verify that the functions f and g are inverses of each other by showing that (f∘g)(x)=x and (g∘f)(x)=x.

  1. f(x)=3x+4; g(x)=13(x−4)

See Student Solutions Manual.

  1. f(x)=x3−8; g(x)=3√x+8

  1. f(x)=1x; g(x)=1x

See Student Solutions Manual.

  1. f(x)=2x+3x+4; g(x)=4x−32−x

In Problems 19–22, (a) determine whether the function is one-to-one. If it is one-to-one, (b) find the inverse of each one-to-one function. (c) State the domain and the range of the function and its inverse.

  1. {(−3,5),(−2,9),(−1,2),(0,11),(1,−5)}

  1. (a) One-to-one
  2. (b) {(5,−3),(9,−2), (2,−1),(11,0),(−5,1)},
  3. (c) Domain of f: {−3,−2,−1,0,1}, range of f: {−5,2,5,9,11}, domain of f−1: {−5,2,5,9,11}, range of f−1: {−3,−2,−1,0,1}

  1. {(−2,2),(−1,6),(0,8),(1,−3),(2,8)}

  1. {(−2,1),(−3,2),(−10,0),(1,9),(2,1)}

  1. (a) Not one-to-one
  2. (b) Does not apply
  3. (c) Domain of f: {−10,−3,−2,1,2}, range of f: {0,1,2,9}

  1. {(−2,−8),(−1,−1),(0,0),(1,1),(2,8)}

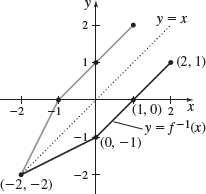
In Problems 23–28, the graph of a one-to-one function f is given. Draw the graph of the inverse function. For convenience, the graph of y=x is also given.

In Problems 29–38, the function f is one-to-one.

  1. (a) Find its inverse and check the result.
  2. (b) Find the domain and the range of f and the domain and the range of f−1.

  1. f(x)=4x+2

  1. (a) f−1(x)=x−24
  2. (b) Both the domain and range of f are (−∞,∞). Both the domain and range of f−1 are (−∞,∞).

  1. f(x)=1−3x

  1. f(x)=3√x+10

  1. (a) f−1(x)=x3−10
  2. (b) Both the domain and range of f are (−∞,∞). Both the domain and range of f−1 are (−∞,∞).

  1. f(x)=2x3+4

  1. f(x)=1x−2

  1. (a) f−1(x)=2+1x
  2. (b) Domain of f: {x|x≠2}, range of f: {y|y≠0}, domain of f−1: {x|x≠0}, range of f−1: {y|y≠2}

  1. f(x)=2x3x−1

  1. f(x)=2x+3x+2

  1. (a) f−1(x)=3−2xx−2
  2. (b) Domain of f: {x|x≠−2}, range of f: {y|y≠2}, domain of f−1: {x|x≠2}, range of f−1: {y|y≠−2}

  1. f(x)=−3x−4x−2

  1. f(x)=x2+4, x≥0

  1. (a) f−1(x)=√x−4
  2. (b) Domain of f: {x|x≥0}, range of f: {y|y≥4}, domain of f−1: {x|x≥4}, range of f−1: {y|y≥0}

  1. f(x)=(x−2)2+4, x≤2