Answers
Chapter P
Section P.1
1. Independent, dependent
2. True
3. False
4. False
5. False
6. Vertical
7. 5,−3
8. −2
9. (a)
10. (a), (b)
11. False
12. 8
13. (a) −4
(b) 3x2−2x−4
(c) −3x2−2x+4
(d) 3x2+8x+1
(e) 3x2+6xh+3h2+2x+2h−4
15. (a) 4
(b) |x|+4
(c) −|x|−4
(d) |x + 1| + 4
(e) |x + h| + 4
17. (−∞,∞)
19. (−∞,−3]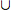 
[3,∞)
21. {x|x ≠ −2, 0, 2}
23. −3
25. 
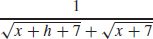
27. 2x + h + 2
29. It is not a function.
31. (a) Domain: [−π, π], range: [−1, 1]
(b) Intercepts: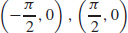 
, (0,1)
(c) Symmetric with respect to the y-axis, but not with respect to the x-axis or the origin.
33. (a) f (−1) = 2, f (0) = 3, f (1) = 5, f (8) = −6
(b)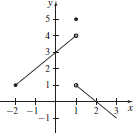 
(c) Domain: [−2,∞), range: (−∞, 4)
{5}, intercepts: (0, 3), (2, 0)
35. (a) f (−1) = 0, f (0) = 0, f (1) = 1, f (8) = 64
(b)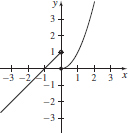 
(c) Domain: (−∞,∞), range: (−∞,∞), intercepts: (−1, 0), (0, 0)
37. f (0) = 3, f (−6) = −3
39. Negative
41. (−3, 6)
(10, 11]
43. [−3, 3]
45. 3
47. Once
49. −5, 8
51. (4, 8)
53. (0, 8)
55. {x|x ≠ 6}
57. −3, (4,−3)
59. −2
61. Odd; symmetric with respect to the origin, but not with respect to the x-axis or the y-axis.
63. Neither; not symmetric to the x-axis, y-axis, or the origin.
65. (a) −4
(b) −8
(c) −10
(d) −2(x + 1)
67. f (x) = 
69. f (x) = 
71. f (x) = 
73. (a) $250.60
(b) $2655.40
(c) Answers will vary.
Section P.2
1. (a)
2. True
3. True
4. False
5. False
6. Zero
7. (b)
8. True
9. True
10. False
11. D
13. F
15. C
17. G
19. (a) 2
(b) 3
(c) −4
21. (a) 7 with multiplicity 1; −4 with multiplicity 3
(b) x-intercepts: 7, −4, y-intercept: −1344
(c) Crosses at 7 and at −4
23. (c), (e), (f)
25. Domain: {x|x ≠ −3}, intercept: (0, 0)
27. Domain: (−∞,∞), intercepts: (0, 0),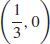 
29. (a) A(x) = 16x − x3
(b) [0, 4]
31. (a) The pattern in the scatter plot suggests a quadratic relationship.
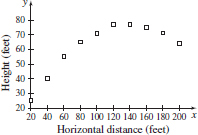
(b) 283.8 feet
(c) 15.63 feet
Section P.3
1. {x|0 ≤ x ≤ 5}
2. False
3. True
4. False
5. True
6. False
7. True
8. Horizontal, right
9. y
10. −5, −2, 2
11. (a) (f + g)(x) = 5x + 1, domain: (−∞,∞)
(b) (f − g)(x) = x + 7, domain: (−∞,∞)
(c) (f ∙ g)(x) = 6x2 − x − 12, domain: (−∞,∞)
(d) 
13. (a) (f + g)(x) =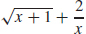 
, domain: {x| − 1 ≤ x < 0}
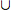{x|x = 0}
(b)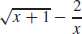 
, domain: {x| − 1 ≤ x < 0}
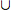{x|x = 0}
(c) (f ∙ g)(x) =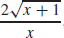 
, domain: {x| − 1 ≤ x < 0}
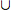{x|x = 0}
(d) 
, domain: {x|x ≥ −1, x = 0}
15. (a) (f ∘ g)(4) = 98
(b) (g ∘ f)(2) = 49
(c) (f ∘ f)(1) = 4
(d) (g ∘ g)(0) = 4
17. (a) (f ∘ g)(1) = −1
(b) (f ∘ g)(−1) = −1
(c) (g ∘ f)(−1) = 8
(d) (g ∘ f)(1) = 8
(e) (g ∘ g)(−2) = 8
(f) (f ∘ f)(−1) = −7
19. (a) (g ∘ f)(−1) = 4
(b) (g ∘ f)(6) = 2
(c) (f ∘ g)(6) = 1
(d) (f ∘ g)(4) = −2
21. (a) (f ∘ g)(x) = 24x + 1, domain: (−∞,∞)
(b) (g ∘ f)(x) = 24x + 8, domain: (−∞,∞)
(c) (f ∘ f)(x) = 9x + 4, domain: (−∞,∞)
(d) (g ∘ g)(x) = 64x, domain: (−∞,∞)
23. (a) (f ∘ g)(x) = x, domain: {x|x ≥ 1}
(b) (g ∘ f)(x) = |x|, domain: (−∞,∞)
(c) (f ∘ f)(x) = x4 + 2x2 + 2, domain: (−∞,∞)
(d) (g ∘ g)(x) =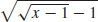 
, domain: {x|x ≥ 2}
25. (a) (f ∘ g)(x) =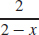 
, domain: {x|x ≠ 0, x ≠ 2}
(b) (g ∘ f)(x) =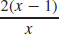 
, domain: {x|x ≠ 0, x ≠ 1}
(c) (f ∘ f)(x) = x, domain: {x|x ≠ 1}
(d) (g ∘ g)(x) = x, domain: {x|x ≠ 0}
27. f (x) = x4, g(x) = 2x + 3
29. f (x) =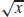 
, g(x) = x2 + 1
31. f (x) = |x|, g(x) = 2x + 1
33. 
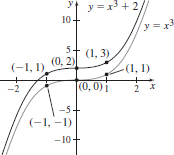
35. 
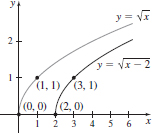
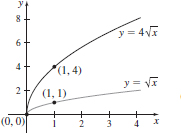
37. 
39. 
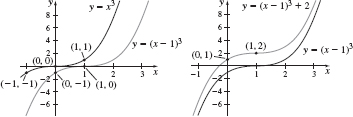
41. 
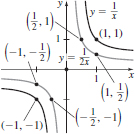
43. 
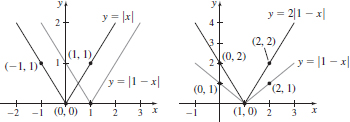
45. 
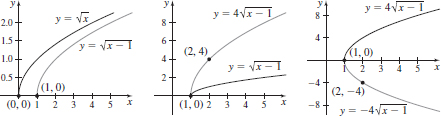
47. (a)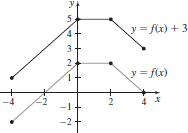 
(b)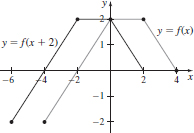 
(c)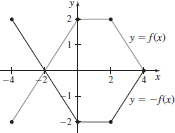 
(d)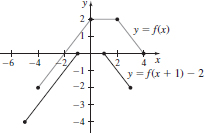 
(e)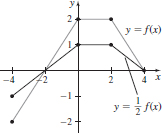 
(f)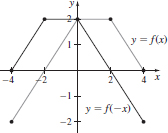 
(g)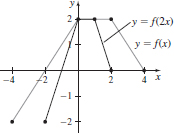 
49. (a)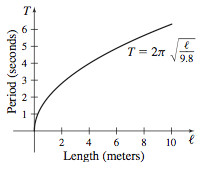 
(b)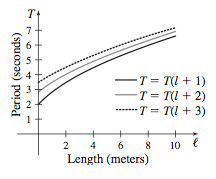 
(c) Answers will vary.
(d)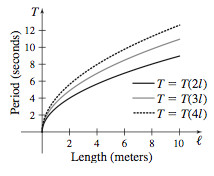 
(e) Answers will vary.
Section P.4
1. False
2. [4,∞)
3. False
4. True
5. False
6. False
7. Answers will vary.
8. Answers will vary.
9. One-to-one
11. Not one-to-one
13. One-to-one
15. See Student Solutions Manual.
17. See Student Solutions Manual.
19. (a) One-to-one
(b) {(5,−3), (9,−2), (2,−1), (11, 0), (−5, 1)},
(c) Domain of f: {−3,−2,−1, 0, 1}, range of f: {−5, 2, 5, 9, 11}, domain of f−1: {−5, 2, 5, 9, 11}, range of f−1: {−3,−2,−1, 0, 1}
21. (a) Not one-to-one
(b) Does not apply
(c) Domain of f: {−10,−3,−2, 1, 2}, range of f: {0, 1, 2, 9}
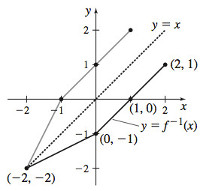
23. 
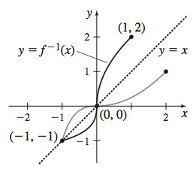
25. 
27. 
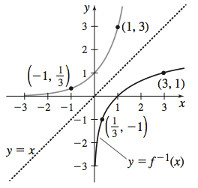
29. (a) f−1 (x) =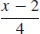 
(b) Both the domain and range of f are (−∞,∞). Both the domain and range of f−1 are (−∞,∞).
31. (a) f−1 (x) = x3 − 10
(b) Both the domain and range of f are (−∞,∞). Both the domain and range of f−1 are (−∞,∞).
33. (a) f−1 (x) = 2 + 
(b) Domain of f: {x|x = 2}, range of f: {y|y = 0}, domain of f−1: {x|x = 0}, range of f−1: {y|y = 2}
35. (a) f−1 (x) =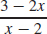 
(b) Domain of f: {x|x = −2}, range of f: {y|y = 2}, domain of f−1: {x|x = 2}, range of f−1: {y|y = −2}
37. (a) f−1 (x) =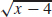 
(b) Domain of f: {x|x ≥ 0}, range of f: {y|y ≥ 4}, domain of f−1: {x|x ≥ 4}, range of f−1: {y|y ≥ 0}
Section P.5
1. 
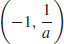, (0, 1), (1, a)
2. False
3. 4
4. 3
5. False
6. False
7. 1
8. {x|x = 0}
9. 
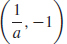, (1, 0), (a, 1)
10. (a)
11. False
12. True
13. True
14. 1
15. Answers will vary.
16. 0
17. (a) g(−1) =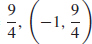 
,
(b) x = 3, (3, 66)
19. (a)
21. (c)
23. (b)
25. Domain: (−∞,∞), range: (0,∞)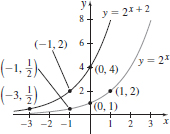
27. Domain: (−∞,∞), range: (0,∞)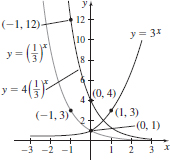
29. Domain: (−∞,∞), range: (0,∞)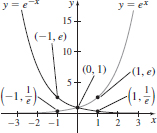
31. {x|x ≠ 0}
33. {x|x = 1}
35. (b)
37. (f)
39. (c)
41. (a) {x|x = −4}
(b and f)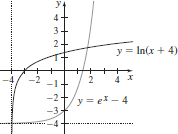
(c) (−∞,∞)
(d) f −1(x) = ex − 4
(e) (−∞,∞)
43. (a) (−∞,∞)
(b and f)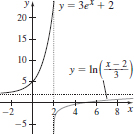
(c) {y|y = 2}
(d) f −1(x) =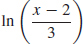 
(e) {y|y = 2}
45. It shifts the x-intercept c units to the left.
47. x = 0, x = 2
49. x = 
51. x =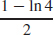 
53. x =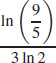 
55. x =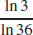 
57. x = 
59. x = 
61. x = 3
63. x ≈ 2.787
65. x ≈ 1.315
67. (a)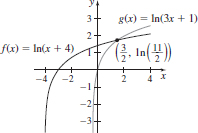 
(b)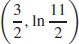 
(c)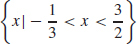 
Section P.6
1. 2π, π
2. All real numbers except odd multiples of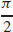 
3. {y| − 1 ≤ y ≤ 1}
4. The period of tan x is π.
5. False
6. 3, 
7. True
8. False
9. True
10. Origin
11. y-axis
12. Answers will vary.
13. −1
15. 
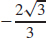
17. 0
19. −1
21. (f)
23. (a)
25. (d)
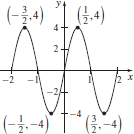
27. 
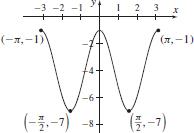
29. 
31. 
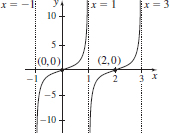
33. 
, 2
35. 3, 2π
37. f (x) = 2 sin(2x)
39. f (x) =
cos(2x)
41. f (x) = −sin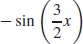 
43. f (x) = 1 – cos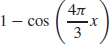 
45. f (x) = cot x
47. f (x) = tan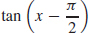 
Section P.7
1. sin y
2. False
3. False
4. True
5. False
6. True
7. True
8. True
9. 
11. 
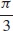
13. 
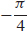
15. 
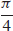
17. 
19. 
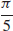
21. 
23. 
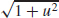
25. See Student Solutions Manual.
27. 
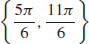
29. 
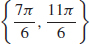
31. 
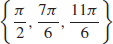
33. 
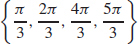
35. 
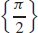
37. 
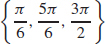
39. 
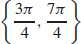
41. 
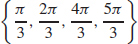
43. 
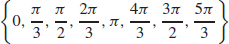
45. {1.373, 4.515}
47. {3.871, 5.553}
49. (a and c)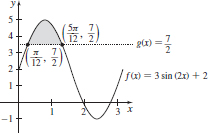 
(b)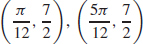 
(c) See (a).
(d) 