1.1 Assess Your UnderstandingPrinted Page 77
77
Concepts and Vocabulary
Multiple Choice The limit as x approaches c of a function f is written symbolically as [(a) lim, (b) \lim\limits_{c \to x} f (x), (c) \lim\limits_{x\to c} f(x)]
(c)
True or False The tangent line to the graph of f at a point P=(c,f(c)) is the limiting position of the secant lines passing through P and a point (x,f(x)), x\neq c, as x moves closer to c.
True
True or False If f is not defined at x=c, then \lim\limits_{x\rightarrow c}f(x) does not exist.
False
True or False The limit L of a function y=f(x) as x approaches the number c depends on the value of f at c.
False
If \lim\limits_{x\rightarrow c}\dfrac{f(x)-f(c)}{x-c} exists, it equals the ______ of the tangent line to the graph of f at the point (c,f(c)).
slope
True or False The limit of a function y=f(x) as x approaches a number c equals L if at least one of the one-sided limits as x approaches c equals L.
False
Skill Building
In Problems 7-12, complete each table and investigate the limit.
\lim\limits_{x\rightarrow 1}2x
\underrightarrow{x~\hbox{approaches 1 from the left}} \underleftarrow{x~\hbox{approaches 1 from the right}} x 0.9 0.09 0.999 \rightarrow 1 \leftarrow 1.001 1.01 1.1 f(x)=2x
\mathop {\lim\limits_{x \to 1}} 2x = 2
| \xrightarrow{x\ {\rm approaches}\ 1\atop \mbox{from the left}} | \xleftarrow{x\ {\rm approaches}\ 1\atop \mbox{from the right}} | ||||||
|---|---|---|---|---|---|---|---|
| x | \ 0.9 | \ 0.99 | 0.999 | \rightarrow 1 \leftarrow | 1.001 | 1.01 | 1.1 |
| f(x)=2x | 1.8 | 1.98 | 1.998 | f(x) approaches 2 | 2.002 | 2.02 | 2.2 |
\lim\limits_{x\rightarrow 2} (x+3)
\underrightarrow{x~\hbox{approaches 2 from the left}} \underleftarrow{x~\hbox{approaches 2 from the right}} x 1.9 1.99 1.999 \rightarrow 2 \leftarrow 2.001 2.01 2.1 f(x)=x+3
\lim\limits_{x\rightarrow 0}( x^{2}+2)
\underrightarrow{x~\hbox{approaches 0 from the left}} \underleftarrow{x~\hbox{approaches 0 from the right}} x -0.1 -0.01 -0.001 \rightarrow 0 \leftarrow 0.001 0.01 0.1 f(x)=x^{2}+2
\mathop {\lim\limits_{x \to 0}} (x^2 + 2) = 2
| \xrightarrow{x\ {\rm approaches}\ 0\atop \mbox{from the left}} | \xleftarrow{x\ {\rm approaches}\ 0\atop \mbox{from the right}} | ||||||
|---|---|---|---|---|---|---|---|
| x | -0.1 | -0.01 | -0.001 | \rightarrow 0 \leftarrow | 0.001 | 0.01 | 0.1 |
| f(x)=x^{2}+2 | 2.01 | 2.0001 | 2.000001 | f(x) approaches 2 | 2.000001 | 2.0001 | 2.01 |
\lim\limits_{x\rightarrow -1} ( x^{2}-2)
\underrightarrow{x~\hbox{approaches –1 from the left}} \underleftarrow{x~\hbox{approaches –1 from the right}} x -1.1 -1.01 -1.001 \rightarrow -1 \leftarrow -0.999 -0.99 -0.9 f(x)=x^{2}-2
\lim\limits_{x\rightarrow -3}\dfrac{x^{2}-9}{x+3}
\underrightarrow{x~\hbox{approaches –3 from the left}} \underleftarrow{x~\hbox{approaches –3 from the right}} x -3.5 -3.1 -3.01 \rightarrow -3 \leftarrow -2.99 -2.9 -2.5 f(x)=\dfrac{x^{2}-9}{x+3}
\mathop {\lim\limits_{x \to - 3}} \dfrac{x^2 - 9}{x + 3} = - 6
| \xrightarrow{x\ {\rm approaches}\ - 3\atop \mbox{from the left}} | \xleftarrow{x\ {\rm approaches}\ -3\atop \mbox{from the right}} | ||||||
|---|---|---|---|---|---|---|---|
| x | -3.5 | -3.1 | -3.01 | \rightarrow -3 \leftarrow | -2.99 | -2.9 | -2.5 |
| f(x)=\dfrac{x^{2}-9}{x+3} | -6.5 | -6.1 | -6.01 | f(x) approaches -6 | -5.99 | -5.9 | -5.5 |
\lim\limits_{x\rightarrow -1}\dfrac{x^{3}+1}{x+1}
\underrightarrow{x~\hbox{approaches –1 from the left}} \underleftarrow{x~\hbox{approaches –1 from the right}} x -1.1 -1.01 -1.001 \rightarrow -1 \leftarrow -0.999 -0.99 -0.9 f(x)=\dfrac{x^{3}+1}{x+1}
![]() In Problems 13-16, use technology to complete the table and investigate the limit.
In Problems 13-16, use technology to complete the table and investigate the limit.
\lim\limits_{x\rightarrow 0}\dfrac{2-2e^{x}}{x}
\underrightarrow{x~\hbox{approaches 0 from the left}} \underleftarrow{x~\hbox{approaches 0 from the right}} x -0.2 -0.1 -0.01 \rightarrow 0 \leftarrow 0.01 0.1 0.2 f(x)=\dfrac{2-2e^{x}}{x}
\mathop {\lim\limits_{x \to 0}} \dfrac{2 - 2e^x}{x} = - 2
| \xrightarrow{x\ {\rm approaches}\ 0\atop \mbox{from the left}} | \xleftarrow{x\ {\rm approaches}\ 0\atop \mbox{from the right}} | ||||||
|---|---|---|---|---|---|---|---|
| x | -0.2 | -0.1 | -0.01 | \rightarrow 0 \leftarrow | 0.01 | 0.1 | 0.2 |
| f(x)=\dfrac{2-2e^{x}}{x} | \kern1pt-1.8127 | -1.9033 | -1.9900 | f(x) approaches -2 | -2.0100 | -2.1034 | -2.2140 |
\lim\limits_{x\rightarrow 1}\dfrac{\ln x}{x-1}
\underrightarrow{x~\hbox{approaches 1 from the left}} \underleftarrow{x~\hbox{approaches 1 from the right}} x 0.9 0.99 0.999 \rightarrow 1 \leftarrow 1.001 1.01 1.1 f(x)=\dfrac{\ln x}{x-1}
\lim\limits_{x\rightarrow 0}\dfrac{1-\cos x}{x}, where x is measured in radians
\underrightarrow{x~\hbox{approaches 0 from the left}} \underleftarrow{x~\hbox{approaches 0 from the right}} x (in radians) -0.2 -0.1 -0.01 \rightarrow 0 \leftarrow 0.01 0.1 0.2 f(x)=\dfrac{1-\cos x}{x}
\mathop {\lim\limits_{x \to 0}} \dfrac{1 - \cos x}{x} = 0
| \xrightarrow{x\ {\rm approaches}\ 0\atop \mbox{from the left}} | \xleftarrow{x\ {\rm approaches}\ 0\atop \mbox{from the right}} | ||||||
|---|---|---|---|---|---|---|---|
| x | -0.2 | -0.1 | -0.01 | \rightarrow 0 \leftarrow | 0.01 | 0.1 | 0.2 |
| f(x)=\dfrac{1-\cos x}{x} | -0.09967 | -0.04996 | -0.00500 | f(x) approaches 0 | 0.00500 | 0.04996 | 0.09967 |
\lim\limits_{x\rightarrow 0}\dfrac{\sin x}{1+\tan x}, where x is measured in radians
\underrightarrow{x~\hbox{approaches 0 from the left}} \underleftarrow{x~\hbox{approaches 0 from the right}} x (in radians) -0.2 -0.1 -0.01 \rightarrow 0 \leftarrow 0.01 0.1 0.2 f(x)=\dfrac{\sin x}{1+\tan x}
78
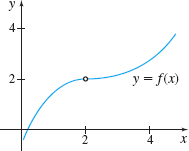
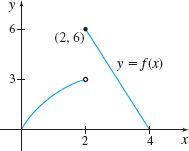
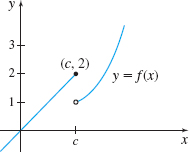
In Problems 17—20, use the graph to investigate
- (a) \lim\limits_{x\rightarrow 2^{-}}f(x),
- (b) \lim\limits_{x\rightarrow 2^{+}}f(x),
- (c) \lim\limits_{x\rightarrow 2}f(x).
- (a) 2
- (b) 2
- (c) 2
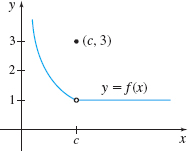
- (a) 3
- (b) 6
- (c) The limit does not exist.
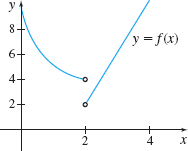
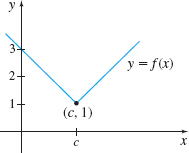
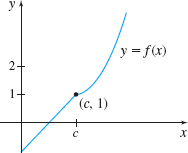
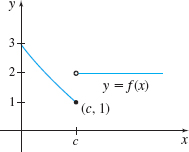
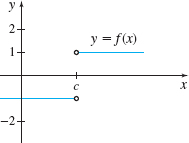
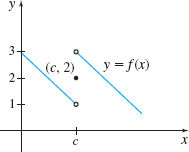
In Problems 21—28, use the graph to investigate \lim\limits_{x\rightarrow c}f(x). If the limit does not exist, explain why.
1
1
The limit does not exist because the two one-sided limits are not equal.
The limit does not exist because the two one-sided limits are not equal.
In Problems 29—36, use a graph to investigate \lim\limits_{x\rightarrow c} f(x) at the number c.
f(x)=\left\{ \begin{array}{l@{\quad}rl} 2x+5 & \hbox{if} & x\leq 2 \\[1pt] 4x+1 & \hbox{if} & x\gt 2 \end{array} \right. at c=2
9
f(x)=\left\{ \begin{array}{c@{\quad}rl} 2x+1 & \hbox{if} & x\leq 0 \\[1pt] 2x & \hbox{if} & x\gt 0 \end{array} \right. at c=0
f(x)=\left\{ \begin{array}{c@{\quad}rl} 3x-1 & \hbox{if} & x\lt 1 \\[1pt] 4 & \hbox{if} & x=1 \\[1pt] 4x & \hbox{if} & x\gt 1 \end{array} \right. at c=1
The limit does not exist.
f(x)=\left\{ \begin{array}{c@{\quad}rl} x+2 & \hbox{if} & x\lt 2 \\[1pt] 4 & \hbox{if} & x=2 \\[1pt] x^{2} & \hbox{if} & x\gt 2 \end{array} \right. at c=2
f(x)=\left\{ \begin{array}{c@{\quad}rl} 2x^{2} & \hbox{if} & x\lt 1 \\[1pt] 3x^{2}-1 & \hbox{if} & x\gt 1 \end{array} \right. at c=1
2
f(x)=\left\{ \begin{array}{c@{}rl} x^{3} & \hbox{if} & x\lt -1 \\[1pt] x^{2}-1 & \hbox{if} & x>-1 \end{array} \right. at c=-1
f(x)=\left\{ \begin{array}{c@{}rl} x^{2} & \hbox{if} & x\leq 0 \\[1pt] 2x+1 & \hbox{if} & x>0 \end{array} \right. at c=0
The limit does not exist.
f(x)=\left\{ \begin{array}{c@{}rl} x^{2} & \hbox{if} & x\lt 1 \\[1pt] 2 & \hbox{if} & x=1 \\[1pt] -3x+2 & \hbox{if} & x>1 \end{array} \right. at c=1
Applications and Extensions
In Problems 37—40, sketch a graph of a function with the given properties. Answers will vary.
\lim\limits_{x\rightarrow 2}f(x) =3; \lim\limits_{x\rightarrow 3^{-}}f(x) =3; \lim\limits_{x\rightarrow 3^{+}}f(x) =1; f(2) =3; f(3) =1
Answers will vary.
\lim\limits_{x\rightarrow -1}f(x) =0; \lim\limits_{x\rightarrow 2^{-}}f(x) =-2; \lim\limits_{x\rightarrow 2^{+}}f(x) =-2; f(-1) is not defined; f(2) =-2
\lim\limits_{x\rightarrow 1}f(x) =4; \lim\limits_{x\rightarrow 0^{-}}f(x) =-1; \lim\limits_{x\rightarrow 0^{+}}f(x) =0; f(0) =-1; f(1) =2
Answers will vary.
\lim\limits_{x\rightarrow 2}f(x) =2; \lim\limits_{x\rightarrow -1}f(x) =0; \lim\limits_{x\rightarrow 1}f(x) =1; f(-1) =1; f(2) =3
79
In Problems 41—50, use either a graph or a table to investigate each limit.
\lim\limits_{x\rightarrow 5^{+}}\dfrac{|x-5|}{x-5}
1
\lim\limits_{x\rightarrow 5^{-}}\dfrac{|x-5|}{x-5}
\lim\limits_{x\rightarrow \left(\frac{1}{2}\right) ^{-}}\lfloor 2x\rfloor
0
{\lim\limits_{x\rightarrow \left(\frac{1}{2}\right) ^{+}}}\lfloor 2x\rfloor
{\lim\limits_{x\rightarrow \left(\frac{2}{3}\right) ^{-}}}\lfloor 2x\rfloor
1
{\lim\limits_{x\rightarrow \left(\frac{2}{3}\right) ^{+}}}\lfloor 2x\rfloor
{\lim\limits_{x\rightarrow 2^{+}}}\ \sqrt{{|}x{|}-x}
0
{\lim\limits_{x\rightarrow 2^{-}}}\ \sqrt{{|}x{|}-x}
{\lim\limits_{x\rightarrow 2^{+}}}\ \sqrt[3]{\lfloor x\rfloor -x}
0
{\lim\limits_{x\rightarrow 2^{-}}}\ \sqrt[3]{\lfloor x\rfloor -x}
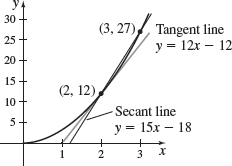
Slope of a Tangent Line For f(x)=3x^{2}:
- (a) Find the slope of the secant line containing the points (2,12) and (3,27).
- (b) Find the slope of the secant line containing the points (2,12) and (x,f(x)), x\neq 2.
- (c) Create a table to investigate the slope of the tangent line to the graph of f at 2 using the result from (b).
- (d) On the same set of axes, graph f, the tangent line to the graph of f at the point (2,12), and the secant line from (a).
- (a) m_{\sec} = 15
- (b) m_{\sec} = 3(x + 2)
- (c) \mathop {\lim\limits_{x \to 2}} m_{\sec } = 12
- (d)
Slope of a Tangent Line For f(x)=x^{3}:
- (a) Find the slope of the secant line containing the points (2,8) and (3,27).
- (b) Find the slope of the secant line containing the points (2,8) and (x,f(x)), x\neq 2.
- (c) Create a table to investigate the slope of the tangent line to the graph of f at 2 using the result from (b).
- (d) On the same set of axes, graph f, the tangent line to the graph of f at the point (2, 8), and the secant line from (a).
Slope of a Tangent Line For f(x)=\dfrac{1}{2}x^{2}-1:
- (a) Find the slope m_{\mathrm{sec}} of the secant line containing the points P=(2,f(2)) and Q=(2+h,f(2+h)).
- (b) Use the result from (a) to complete the following table:
h -0.5 -0.1 -0.001 0.001 0.1 0.5 m_{\sec } - (c) Investigate the limit of the slope of the secant line found in (a) as h\rightarrow 0.
- (d) What is the slope of the tangent line to the graph of f at the point P=(2,f(2))?
- (e) On the same set of axes, graph f and the tangent line to f at P=(2,f(2)).
- (a) m_{\sec } = 2 + \dfrac{1}{2}h\mbox{ for }h \ne 0
- (b)
{h} {-0.5} {-0.1} {-0.001} {0.001} {0.1} {0.5} m_{\sec } 1.75 1.95 1.9995 2.0005 2.05 2.25 - (c) \mathop {\lim\limits_{h \to 0}} m_{\sec } = 2
- (d) m_{\tan} = 2
- (e)

Slope of a Tangent Line For f(x)=x^{2}-1:
- (a) Find the slope m_{\mathrm{sec}} of the secant line containing the points P=(-1,f(-1)) and Q=(-1+h,f(-1+h)).
- (b) Use the result from (a) to complete the following table:
h -0.1 -0.01 -0.001 -0.0001 0.0001 0.001 0.01 0.1 msec - (c) Investigate the limit of the slope of the secant line found in (a) as h\rightarrow 0.
- (d) What is the slope of the tangent line to the graph of f at the point P=(-1,f(-1) )?
- (e) On the same set of axes, graph f and the tangent line to f at P=(-1,f(-1)).
- (a) Investigate \lim\limits_{x\rightarrow 0}\cos \dfrac{\pi}{x} by using a table and evaluating the function f(x) =\cos \dfrac{\pi }{x} at x =-\dfrac{1}{2}, -\dfrac{1}{4}, - \dfrac{1}{8}, -\dfrac{1}{10}, -\dfrac{1}{12},\ldots, \dfrac{1}{12}, \dfrac{1}{10}, \dfrac{1}{8}, \dfrac{1}{4}, \dfrac{1}{2}.
- (b) Investigate \lim\limits_{x\rightarrow 0}\cos \dfrac{\pi }{x} by using a table and evaluating the function f(x) =\cos \dfrac{\pi }{x} at x=-1,-\dfrac{1}{3}, -\dfrac{1}{5}, -\dfrac{1}{7}, - \dfrac{1}{9},\ldots,\dfrac{1}{9},\dfrac{1}{7}, \dfrac{1}{5}, \dfrac{1}{3},1.
- (c) Compare the results from (a) and (b). What do you conclude about the limit? Why do you think this happens? What is your view about using a table to draw a conclusion about limits?
- (d)
 Use graphing technology to graph f. Begin with the x -window [-2\pi ,2\pi ] and the y-window [-1,1]. If you were finding \lim\limits_{x\rightarrow 0}f(x) using a graph, what would you conclude? Zoom in on the graph. Describe what you see. ({Hint}: Be sure your calculator is set to the radian mode.)
Use graphing technology to graph f. Begin with the x -window [-2\pi ,2\pi ] and the y-window [-1,1]. If you were finding \lim\limits_{x\rightarrow 0}f(x) using a graph, what would you conclude? Zoom in on the graph. Describe what you see. ({Hint}: Be sure your calculator is set to the radian mode.)
- (a) These values suggest that \mathop {\lim\limits_{x \to 0}} \cos \dfrac{\pi}{x} = 1.
- (b) These values suggest \mathop {\lim\limits_{x \to 0}} \cos \dfrac{\pi}{x} = - 1
- (c) \mathop {\lim\limits_{x \to 0}} \cos \dfrac{\pi}{x} does not exist. Answers will vary.
- (d) Answers will vary.
- (a) Investigate \lim\limits_{x\rightarrow 0}\cos \dfrac{ \pi }{x^{2}} by using a table and evaluating the function f(x) =\cos \dfrac{\pi }{x^{2}} at x=-0.1, -0.01, -0.001, -0.0001, 0.0001, 0.001, 0.01, 0.1.
- (b) Investigate \lim\limits_{x\rightarrow 0}\cos \dfrac{\pi }{x^{2} } by using a table and evaluating the function f(x) =\cos \dfrac{\pi }{x^{2}} at x=-\dfrac{2}{3}, -\dfrac{2}{5}, -\dfrac{2}{7}, -\dfrac{2}{9}, \ldots, \dfrac{2}{9},\dfrac{2}{7}, \dfrac{2}{5}, \dfrac{2 }{3}.
- (c) Compare the results from (a) and (b). What do you conclude about the limit? Why do you think this happens? What is your view about using a table to draw a conclusion about limits?
- (d)
 Use graphing technology to graph f. Begin with the x -window \left[ -2\pi ,2\pi \right] and the y-window [-1,1]. If you were finding \lim\limits_{x\rightarrow 0}f(x) using a graph, what would you conclude? Zoom in on the graph. Describe what you see. ({Hint}: Be sure your calculator is set to the radian mode.)
Use graphing technology to graph f. Begin with the x -window \left[ -2\pi ,2\pi \right] and the y-window [-1,1]. If you were finding \lim\limits_{x\rightarrow 0}f(x) using a graph, what would you conclude? Zoom in on the graph. Describe what you see. ({Hint}: Be sure your calculator is set to the radian mode.)
- (a) Use a table to investigate \lim\limits_{x\rightarrow 2}\dfrac{x-8}{2}.
- (b) How close must x be to 2, so that f(x) is within 0.1 of the limit?
80
- (c) How close must x be to 2, so that f(x) is within 0.01 of the limit?
- (a) The table suggests \mathop {\lim\limits_{x \to 2}} \dfrac{x - 8}{2} = - 3
- (b) 1.8 \leq x \leq 2.2
- (c) 1.98 \leq x \leq 2.02
| \xrightarrow{x\ {\rm approaches}\ 2\atop \mbox{from the left}} | \xleftarrow{x\ {\rm approaches}\ 2\atop \mbox{from the right}} | ||||||
|---|---|---|---|---|---|---|---|
| x | 1.9 | 1.99 | 1.999 | \rightarrow 2 \leftarrow | 2.001 | 2.01 | 2.1 |
| f(x)=\dfrac{x - 8}{2} | -3.05 | -3.005 | -3.0005 | f(x) approaches -3 | -2.9995 | -2.995 | -2.95 |
- (a) Use a table to investigate \lim\limits_{x\rightarrow 2} (5-2x).
- (b) How close must x be to 2, so that f(x) is within 0.1 of the limit?
- (c) How close must x be to 2, so that f(x) is within 0.01 of the limit?
First-Class Mail As of January 2013, the U.S. Postal Service charged $0.46 postage for first-class letters weighing up to and including 1 ounce, plus a flat fee of $0.20 for each additional or partial ounce up to and including 3.5 ounces. First-class letter rates do not apply to letters weighing more than 3.5 ounces.
 Source: U.S. Postal Service Notice 123.
Source: U.S. Postal Service Notice 123.- (a) Find a function C that models the first-class postage charged, in dollars, for a letter weighing w ounces. Assume w>0.
- (b) What is the domain of C?
- (c) Graph the function C.
- (d) Use the graph to investigate \lim\limits_{w\rightarrow 2^{-}}C(w) and \lim\limits_{w\rightarrow 2^{+}}C(w). Do these suggest that \lim\limits_{w\rightarrow 2} C(w) exists?
- (e) Use the graph to investigate \lim\limits_{w\rightarrow 0^{+}}C(w).
- (f) Use the graph to investigate \lim\limits_{w\rightarrow 3.5^{-}}C(w).
- (a) C(w) = \left\{ \begin{array}{@{}ll@{\quad}rcl@{}} {0.46} &\hbox{if} & 0 &<& w \le 1 \\ {0.66}&\hbox{if} & 1 &<& w \le 2 \\ {0.86}&\hbox{if} & 2 &<& w \le 3\\ {1.06}&\hbox{if} & 3 &<& w \le 3.5\\ \end{array} \right.
- (b) {\{} w \vert 0 < w \le 3.5 {\}}
- (c) See the graph below.
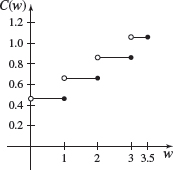
- (d) The graph suggests \lim\limits_{w\to2^{-}}C(w)=0.66, \lim\limits_{w\to2^{+}}C(w)=0.86, \lim\limits_{w\to2}C(w) does not exist.
- (e) The graph suggests \lim\limits_{w\to0^{+}}C(w)=0.46
- (f) The graph suggests \lim\limits_{w\to3.5^{-}}C(w)=1.06
First-Class Mail As of January 2013, the U.S. Postal Service charged $0.92 postage for first-class retail flats (large envelopes) weighing up to and including 1 ounce, plus a flat fee of $0.20 for each additional or partial ounce up to and including 13 ounces. First-class rates do not apply to flats weighing more than 13 ounces.
- (a) Find a function C that models the first-class postage charged, in dollars, for a large envelope weighing w ounces. Assume w\gt 0.
- (b) What is the domain of C?
- (c) Graph the function C.
- (d) Use the graph to investigate \lim\limits_{w\rightarrow 1^{-}}C(w) and \lim\limits_{w\rightarrow 1^{+}}C(w). Do these suggest that \lim\limits_{w\rightarrow 1} C(w) exists?
- (e) Use the graph to investigate \lim\limits_{w\rightarrow 12^{-}}C(w) and \lim\limits_{w\rightarrow 12^{+}}C(w). Do these suggest that \lim\limits_{w\rightarrow 12} C(w) exists?
- (f) Use the graph to investigate \lim\limits_{w\rightarrow 0^{+}}C(w).
- (g) Use the graph to investigate \lim\limits_{w\rightarrow 13^{-}}C(w).
Source: U.S. Postal Service Notice 123.
Correlating Student Success to Study Time Professor Smith claims that a student's final exam score is a function of the time t (in hours) that the student studies. He claims that the closer to seven hours one studies, the closer to 100% the student scores on the final. He claims that studying significantly less than seven hours may cause one to be underprepared for the test, while studying significantly more than seven hours may cause ''burnout.''
- (a) Write Professor Smith's claim symbolically as a limit.
- (b) Write Professor Smith's claim using the \epsilon-\delta definition of limit.
Source: Submitted by the students of Millikin University.
- (a) \mathop {\lim\limits_{t \to 7} } S(t) = 100
- (b) Given any \varepsilon > 0, there is a number \delta > 0 so that whenever 0 < \vert t -7 \vert < \delta then \vert S(t) -100 \vert < \varepsilon .
The definition of the slope of the tangent line to the graph of y=f(x) at the point (c,f(c)) is m_{\tan }=\lim\limits_{x\rightarrow c}\dfrac{f(x) -f(c) }{x-c}. Another way to express this slope is to define a new variable h=x-c. Rewrite the slope of the tangent line m_{\tan } using h and c.
If f(2) =6, can you conclude anything about \lim\limits_{x\rightarrow 2}f(x) ? Explain your reasoning.
Answers will vary.
If \lim\limits_{x\rightarrow 2}f(x) =6, can you conclude anything about f(2) ? Explain your reasoning.
The graph of f(x) ={\dfrac{{x-3}}{{3-x}}} is a straight line with a point punched out.
- (a) What straight line and what point?
- (b) Use the graph of f to investigate the one-sided limits of f as x approaches 3.
- (c) Does the graph suggest that \lim\limits_{x\rightarrow 3}f(x) exists? If so, what is it?
- (a) The graph of f(x) is the horizontal line y = -1 excluding the point (3, -1).
- (b) \mathop {\lim\limits_{x \to 3^ - } } f(x) = \mathop {\lim \limits_{x \to 3^ + }}f(x) = - 1.
- (c) The graph suggests \mathop {\lim\limits_{x \to 3} } f(x) = -1.

- (a) Use a table to investigate \lim\limits_{x \rightarrow 0}(1+x) ^{1/x}.
- (b) Use graphing technology to graph g(x) =(1+x) ^{1/x}.
- (c) What do (a) and (b) suggest about \lim\limits_{x\rightarrow 0}(1+x) ^{1/x}?
- (d)
 Find \lim\limits_{x\rightarrow 0}(1+x) ^{1/x}.
Find \lim\limits_{x\rightarrow 0}(1+x) ^{1/x}.
Challenge Problems
For Problems 67—70, investigate each of the following limits. f(x) ={\left\{ \begin{array}{c@{\qquad}l} 1 & \hbox{if }x\hbox{ is an integer} \\ 0 & \hbox{if }x\hbox{ is not an integer} \end{array} \right. }
\lim\limits_{x\rightarrow 2}f(x)
0
\lim\limits_{x\rightarrow 1/2}f(x)
\lim\limits_{x\rightarrow 3}f(x)
0
\lim\limits_{x\rightarrow 0}f(x)