Processing math: 0%

1.3 Assess Your Understanding

Printed Page 102

Concepts and Vocabulary

  1. True or False A polynomial function is continuous at every real number.

True

  1. True or False Piecewise-defined functions are never continuous at numbers where the function changes equations.

False

  1. The three conditions necessary for a function f to be continuous at a number c are _______, _______, and _______.

f(c) is defined, lim exists, \mathop {\lim\limits_{x \to c}} f(x) = f(c)

  1. True or False If f(x) is continuous at 0, then g(x)=\dfrac{1}{4}f(x) is continuous at 0.

True

  1. True or False If f is a function defined everywhere in an open interval containing c, except possibly at c, then the number c is called a removable discontinuity of f if the function f is not continuous at c.

False

  1. True or False If a function f is discontinuous at a number c, then \lim\limits_{x\rightarrow c}f( x) does not exist.

False

  1. True or False If a function f is continuous on an open interval (a,b), then it is continuous on the closed interval [a,b].

False

  1. True or False If a function f is continuous on the closed interval [a,b], then f is continuous on the open interval (a,b).

True

In Problems 9 and 10, explain whether each function is continuous or discontinuous on its domain.

  1. The velocity of a ball thrown up into the air as a function of time, if the ball lands 5 seconds after it is thrown and stops.

The function is discontinuous.

  1. The temperature of an oven used to bake a potato as a function of time.

The function is continuous.

  1. True or False If a function f is continuous on a closed interval [ a,b], then the Intermediate Value Theorem guarantees that the function takes on every value between f(a) and f(b).

True

  1. True or False If a function f is continuous on a closed interval [a, b] and f( a) \neq f( b), but both f( a) >0 and f( b) >0, then according to the Intermediate Value Theorem, f does not have a zero on the open interval ( a,b).

False

Skill Building

In Problems 13-18, use the accompanying graph of y=f(x).

  1. (a) Determine if f is continuous at c.
  2. (b) If f is discontinuous at c, state which condition(s) of the definition of continuity is (are) not satisfied.
  3. (c) If f it is discontinuous at c, determine if the discontinuity is removable.
  4. (d) If the discontinuity is removable, define (or redefine) f at c to make f continuous at c.

  1. c=-3

  1. (a) The function is not continuous at c = -3.
  2. (b) \mathop {\lim\limits_{x \to - 3}} f(x) \ne f( - 3)
  3. (c) The discontinuity is removable.
  4. (d) f(-3) = -2

  1. c=0

  1. c=2

  1. (a) The function is not continuous at c = 2.
  2. (b) \mathop {\lim\limits_{x \to 2}} f(x) does not exist.
  3. (c) The discontinuity is not removable.

  1. c=3

  1. c=4

  1. (a) The function is continuous at c = 4.

  1. c=5

In Problems 19-32, determine whether the function f is continuous at c.

  1. {f}( x) = x^2+1  at c=-1

The function is continuous at c = -1.

  1. {f}( x) = x^3-5  at c=5

  1. f(x)=\dfrac{x}{x^{2}+4} at c=-2

The function is continuous at c = -2.

  1. f(x)=\dfrac{x}{x-2} at c=2

  1. f(x)=\left\{ \begin{array}{l@{\quad}l} 2x+5 & \hbox{if }x\leq 2 \\[3pt] 4x+1 & \hbox{if }x>2 \end{array} \right.  at c=2

The function is continuous at c = 2.

  1. f(x)=\left\{ \begin{array}{l@{\quad}l} 2x+1 & \hbox{if }x\leq 0 \\[3pt] 2x & \hbox{if }x>0 \end{array} \right. at c=0

  1. f(x)=\left\{ \begin{array}{c@{\quad}l} 3x-1 & \hbox{if }x\lt 1 \\[3pt] 4 & \hbox{if }x=1 \\[3pt] 2x & \hbox{if }x>1 \end{array} \right.  at c=1

The function is not continuous at c = 1.

  1. f(x)=\left\{ \begin{array}{c@{\quad}l@{\quad}l} 3x-1 & \hbox{if }x\lt 1 \\[3pt] 2 & \hbox{if }x=1 & \hbox{at}\ c=1\\[3pt] 2x & \hbox{if }x>1 \end{array} \right.

  1. f(x)=\left\{ \begin{array}{l@{\quad}l} 3x-1 & \hbox{if }x\lt 1 \\[3pt] 2x & \hbox{if }x>1 \end{array} \right. at c=1

The function is not continuous at c = 1.

  1. f(x)=\left\{ \begin{array}{c@{\quad}l} 3x-1 & \hbox{if }x\lt 1 \\[3pt] 2 & \hbox{if }x=1 \\[3pt] 3x & \hbox{if }x>1 \end{array} \right. at c=1

  1. f(x)=\left\{ \begin{array}{l@{\quad}l} x^{2} & \hbox{if }x\leq 0 \\[3pt] 2x & \hbox{if }x>0 \end{array} \right. at c=0

The function is continuous at c = 0.

  1. f(x)=\left\{ \begin{array}{c@{\quad}l} x^{2} & \hbox{if }x\lt -1 \\[3pt] 2 & \hbox{if }x=-1 \\[3pt] -3x+2 & \hbox{if }x>-1 \end{array} \right. at c=-1

  1. f(x)=\left\{ \begin{array}{c@{\quad}l} 4-3x^{2} & \hbox{if }x\lt 0 \\ 4 & \hbox{if }x=0 \\[3pt] \sqrt{\dfrac{16-x^{2}}{4-x}} & \hbox{if }0\lt x\lt 4 \end{array} \right.  at c=0

The function is not continuous at c = 0.

103

  1. f(x)=\left\{ \! \begin{array}{l@{\ \ }l} \sqrt{4+x} & \hbox{if \(-4\)}\leq x\leq 4 \\[3pt] \sqrt{\dfrac{x^{2}-3x-4}{x-4}} & \hbox{if } x>4 \end{array} \right. at c=4

In Problems 33-36, each function f has a removable discontinuity at c. Define f(c) so that f is continuous at c.

  1. {f}( x) =\dfrac{x^{2}-4}{x-2}, c=2

f(2) = 4

  1. {f}( x) =\dfrac{x^{2}+x-12}{x-3}, c=3

  1. f(x)=\left\{ \begin{array}{l@{\quad}l} 1+x & \hbox{if }x \lt 1 \\[3pt] 4 & \hbox{if } x=1\\[3pt] 2x & \hbox{if }x>1 \end{array} \right.  c=1

f(1) = 2

  1. f(x)=\left\{ \begin{array}{l@{\quad}l} x^{2}+5x & \hbox{if }x\lt -1 \\ 0 & \hbox{if } x=-1\\[3pt] x-3 & \hbox{if }x>-1 \end{array} \right. c=-1

In Problems 37-40, determine whether each function f is continuous on the given interval.

  1. {f}( x) =\dfrac{x^{2}-9}{x-3} on the interval [ -3,3)

The function is continuous on the given interval.

  1. {f}( x) =1+\dfrac{1}{x} on the interval [-1,0)

  1. {f}( x) =\dfrac{1}{\sqrt{x^{2}-9}} on the interval [ -3,3]

The function is not continuous on the given interval.

  1. {f}( x) =\sqrt{9-x^{2}} on the interval [ -3,3]

In Problems 41-50, determine where each function f is continuous. First determine the domain of the function. Then support your decision using properties of continuity.

  1. f( x) =2x^{2}+5x-\dfrac{1}{x}

The function is continuous on \{x\vert x \ne 0\}.

  1. f( x) =x+1+\dfrac{2x}{x^{2}+5}

  1. f( x) =( x-1) (x^{2}+x+1)

The function is continuous on the set of all real numbers.

  1. f( x) =\sqrt{x} (x^{3}-5)

  1. f(x)=\dfrac{x-9}{\sqrt{x}-3}

The function is continuous on \{ x \vert x \ge 0, x \ne 9\}.

  1. f(x)={\dfrac{{x-4}}{{\sqrt{x}-2}}}

  1. f(x)=\sqrt{{\dfrac{{x^{2}+1}}{{2-x}}}}

The function is continuous on the set \{ x \vert x < 2 \}.

  1. f(x)=\sqrt{{\dfrac{{4}}{{x^{2}-1}}}}

  1. f( x) = (2x^{2}+5x-3) ^{2/3}

The function is continuous on the set of all real numbers.

  1. f( x) =( x+2) ^{1/2}

In Problems 51-56, use the function \begin{equation*} f(x)={\left\{ \begin{array}{c@{\qquad}l} \sqrt{15-3x} & \hbox{if}\ x\lt 2 \\ \sqrt{5} & \hbox{if}\ x=2 \\ 9-x^{2} & \hbox{if}\ 2\lt x\lt 3 \\ \lfloor x-2\rfloor & \hbox{ if }\ 3\leq x \end{array} \right. } \end{equation*}

  1. Is f continuous at 0? Why or why not?

f is continuous at 0 because \mathop {\lim\limits_{x \to 0}} f(x) = f(0).

  1. Is f continuous at 4? Why or why not?

  1. Is f continuous at 3? Why or why not?

f is not continuous at 3 because \mathop {\lim\limits_{x \to 3}} f(x) does not exist.

  1. Is f continuous at 2? Why or why not?

  1. Is f continuous at 1? Why or why not?

f is continuous at 1 because \mathop {\lim\limits_{x \to 1}} f(x) = f(1).

  1. Is f continuous at 2.5? Why or why not?

In Problems 57 and 58:

  1. (a) Use graphing technology to graph f using a suitable scale on each axis.
  2. (b) Based on the graph from (a), determine where f is continuous.
  3. (c) Use the definition of continuity to determine where f is continuous.
  4. (d) What advice would you give a fellow student about using graphing technology to determine where a function is continuous?

  1. f( x) =\dfrac{x^{3}-8}{x-2}

  1. (a)
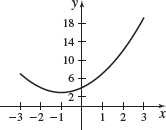
  2. (b) Based on the graph, it appears that the function is continuous for all real numbers.
  3. (c) f is actually continuous at all real numbers except x = 2.
  4. (d) Answers will vary.

  1. f( x) =\dfrac{x^{2}-3x+2}{3x-6}

In Problems 59-64, use the Intermediate Value Theorem to determine which of the functions must have zeros in the given intervals. Indicate those for which the theorem gives no information. Do not attempt to locate the zeros.

  1. f(x)=x^{3}-3x on {[{-2,2}]}

Yes. A zero exists on the given interval.

  1. f(x)=x^{4}-1 on {[{-2,2}]}

  1. f(x)={\dfrac{{x}}{{({x+1})^{2}}}}-1 on [ 10,20]

The IVT gives no information.

  1. f(x)=x^{3}-2x^{2}-x+2 on {[{3,4}]\qquad }

  1. f( x) =\dfrac{x^{3}-1}{x-1} on [ 0,2]

The IVT gives no information.

  1. f(x)=\dfrac{x^{2}+3x+2}{ x^{2}-1} on {[-{3,0}]}

In Problems 65-72, verify each function has a zero in the indicated interval. Then use the Intermediate Value Theorem to approximate the zero correct to three decimal places by repeatedly subdividing the interval containing the zero into 10 subintervals.

  1. f( x) = x^{3}+3x-5; interval: ( 1,2)

1.154

  1. f( x) =x^{3}-4x+2; interval: (1 ,2)

  1. f( x) =2x^{3}+3x^{2}+4x-1; interval: (0,1)

0.211

  1. f( x) =x^{3}-x^{2}-2x+1; interval: (0,1)

  1. f( x) =x^{3}-6x-12; interval:(3,4)

3.134

  1. f( x) =3x^{3}+5x-40; interval: (2,3)

  1. f( x) =x^{4}-2x^{3}+21x-23; interval: ( 1,2)

1.157

  1. f( x) =x^{4}-x^{3}+x-2; interval: ( 1,2)

In Problems 73 and 74,

  1. (a) Use the Intermediate Value Theorem to show that f has a zero in the given interval.
  2. (b) Use technology to find the zero rounded to three decimal places.

  1. f( x) =\sqrt{x^{2}+4x}-2 in (0, 1)

  1. (a) Since f is continuous on [0, 1], f(0) < 0, and f(1) > 0, the IVT guarantees that f must have a zero on the interval (0, 1).
  2. (b) 0.828

  1. f(x)=x^{3}-x+2 in (-2, 0)

Applications and Extensions

Heaviside Functions In Problems 75 and 76, determine whether the given Heaviside function is continuous at c.

  1. u_{1}( t) =\left\{ \begin{array}{l@{\quad}l} 0 & \hbox{if }t\lt 1 \\[3pt] 1 & \hbox{if }t\geq 1 \end{array} \right.\quad c=1

The function is not continuous at c = 1.

104

  1. u_{3}( t) =\left\{ \begin{array}{l@{\quad}l} 0 & \hbox{if }t\lt 3 \\ 1 & \hbox{if }t \geq 3 \end{array} \quad c=3\right.

In Problems 77 and 78, determine where each function is continuous. Graph each function.

  1. f(x)=\left\{ \begin{array}{l@{\quad}l} 1-x^{2} & \hbox{if }\vert x\vert \leq 1 \\ x^{2}-1 & \hbox{if }\vert x\vert >1 \end{array} \right.

The function is continuous on the set of all real numbers.

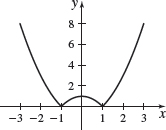
  1. f(x)=\left\{ \begin{array}{c@{\quad}c} \sqrt{4-x^{2}} & \hbox{if }\vert x\vert \leq 2 \\ \left\vert \,x\,\right\vert -2 & \hbox{if }\vert x\vert >2 \end{array} \right.

  1. First-Class Mail As of January 2013, the U.S. Postal Service charged $0.46 postage for first-class letters weighing up to and including 1 ounce, plus a flat fee of $0.20 for each additional or partial ounce up to 3.5 ounces. First-class letter rates do not apply to letters weighing more than 3.5 ounces.

    1. (a) Find a function C that models the first-class postage charged for a letter weighing w ounces. Assume w>0.
    2. (b) What is the domain of C?
    3. (c) Determine the intervals on which C is continuous.
    4. (d) At numbers where C is not continuous, what type of discontinuity does C have?
    5. (e) What are the practical implications of the answer to (d)?

    Source: U.S. Postal Service Notice 123.

  1. (a) C(w) = \left\{ \begin{array}{l@{\quad}rcl} {0.46,} & 0 &<& w \le 1 \\ {0.66,} & 1 &<& w \le 2 \\ {0.86,} & 2 &<& w \le 3\\ {1.06,} & 3 &<& w \le 3.5\\ \end{array} \right.
  2. (b) {\{} w \vert 0 < w \le 3.5 {\}}
  3. (c) The function is continuous on the intervals (0, 1], (1, 2], (2, 3], and (3, 3.5].
  4. (d) At w = 1, w = 2, and w = 3, the function has a jump discontinuity.
  5. (e) Answers will vary.

  1. First-Class Mail As of January 2013, the U.S. Postal Service charged $0.92 postage for first-class retail flats (large envelopes) weighing up to and including 1 ounce, plus a flat fee of $0.20 for each additional or partial ounce up to 13 ounces. First-class rates do not apply to flats weighing more than 13 ounces.

    1. (a) Find a function C that models the first-class postage charged for a large envelope weighing w ounces. Assume w>0.
    2. (b) What is the domain of C?
    3. (c) Determine the intervals on which C is continuous.
    4. (d) At numbers where C is not continuous (if any), what type of discontinuity does C have?
    5. (e) What are the practical implications of the answer to (d)?

    Source: U.S. Postal Service Notice 123.

  1. Cost of Natural Gas In February 2012 Peoples Energy had the following monthly rate schedule for natural gas usage in single- and two-family residences with a single gas meter:

    Monthly customer charge $22.13
    Per therm distribution charge
     \leq 50 therms $0.25963 per therm
     >50 therms $12.98 + 0.11806 for each therm in excess of 50
    Gas charge $0.3631 per therm

    Source: Peoples Energy, Chicago, IL.

    1. (a) Find a function C that models the monthly cost of using x therms of natural gas.
    2. (b) What is the domain of C?
    3. (c) Determine the intervals on which C is continuous.
    4. (d) At numbers where C is not continuous (if any), what type of discontinuity does C have?
    5. (e) What are the practical implications of the answer to (d)?

  1. (a) C(x) = \left\{ \begin{array}{l@{\quad}rcl} {22.13 + 0.62273x,} & \mbox{0} &<& x \le \mbox{50} \\ {29.207 + 0.48116x,} & x &>& \mbox{50} \\ \end{array} \right.
  2. (b) {\{}x \vert x > 0{\}}
  3. (c) C(x) is continuous on its domain.
  4. (d) See (c).
  5. (e) Answers will vary.

  1. Cost of Water The Jericho Water District determines quarterly water costs, in dollars, using the following rate schedule:

    Water used (in thousands of gallons) Cost
    0\leq x\leq 10 $9.00
    10\lt x\leq 30 $9.00+0.95 for each thousand gallons in excess of 10{,}000 gallons
    30\lt x\leq 100 $28.00+1.65 for each thousand gallons in excess of 30{,}000 gallons
    x>100 $143.50+2.20 for each thousand gallons in excess of 100{,}000 gallons

    Source: Jericho Water District, Syosset, NY.

    1. (a) Find a function C that models the quarterly cost of using x thousand gallons of water.
    2. (b) What is the domain of C?
    3. (c) Determine the intervals on which C is continuous.
    4. (d) At numbers where C is not continuous (if any), what type of discontinuity does C have?
    5. (e) What are the practical implications of the answer to (d)?

  1. Gravity on Europa Europa, one of the larger satellites of Jupiter, has an icy surface and appears to have oceans beneath the ice. This makes it a candidate for possible extraterrestrial life. Because Europa is much smaller than most planets, its gravity is weaker. If we think of Europa as a sphere with uniform internal density, then inside the sphere, the gravitational field g is given by g( r) =\dfrac{Gm}{R^{3}}r, 0\leq r\lt R, where R is the radius of the sphere, r is the distance from the center of the sphere, and G is the universal gravitation constant. Outside a uniform sphere of mass m, the gravitational field g is given by g( r) =\dfrac{Gm}{r^{2}}, R\lt r.

    1. (a) For the gravitational field of Europa to be continuous at its surface, what must g(r) equal? [Hint: Investigate \lim\limits_{r\rightarrow R}g( r).]
    2. (b) Determine the gravitational field at Europa's surface. This will indicate the type of gravity environment organisms will experience. Use the following measured values: Europa's mass is 4.8\times 10^{22}kilograms, its radius is 1.569 \times 10^6 meters, and G=6.67\times 10^{-11}.
    3. (c) Compare the result found in (b) to the gravitational field on Earth's surface, which is 9.8 meter/second^2. Is the gravity on Europa less than or greater than that on Earth?

  1. (a) \dfrac{Gm}{R^2}
  2. (b) 1.3 m/s^{2}
  3. (c) Answers will vary.

105

  1. Find constants A and B so that the function below is continuous for all x. Graph the resulting function. \begin{equation*} f(x)=\left\{ \begin{array}{c@{\qquad}lrll} ( x-1) ^{2} & \hbox{if } &- \infty&\lt x\lt 0 \\ \left( A-x\right) ^{2} & \hbox{if }&0&\leq x\lt 1 \\ x+B & \hbox{if }&1&\leq x\lt \infty \end{array} \right. \end{equation*}

  1. Find constants A and B so that the function below is continuous for all x. Graph the resulting function.\begin{equation*} f(x)=\left\{ \begin{array}{c@{\qquad}lrll} x+A & \hbox{if }&-\infty &\lt x\lt 4 \\ ( x-1) ^{2} & \hbox{if }&4&\leq x\leq 9 \\ Bx+1 & \hbox{if }&9&\lt x\lt \infty \end{array} \right. \end{equation*}

A = 5, B = 7

  1. For the function f below, find k so that f is continuous at 2. \begin{equation*} f(x)=\left\{ \begin{array}{c@{\qquad}l} \dfrac{\sqrt{2x+5}-\sqrt{x+7}}{x-2}, &x\geq -\dfrac{5}{2}, x\neq 2 \\ k & \hbox{if }\ x=2\end{array} \right. \end{equation*}

  1. Suppose f(x) ={\dfrac{{x^{2}-6x-16}}{{( {x^{2}-7x-8}) \sqrt{x^{2}-4}}}}.

    1. (a) For what numbers x is f defined?
    2. (b) For what numbers x is f discontinuous?
    3. (c) Which discontinuities found in (b) are removable?

  1. (a) {\{}x \vert x < 2{\}}\cup {\{}x \vert x > 2, x \ne 8{\}}
  2. (b) f is discontinuous at x = 8.
  3. (c) The discontinuity at x = 8 is removable.

  1. Intermediate Value Theorem

    1. (a) Use the Intermediate Value Theorem to show that the function f(x)=\sin x+x-3 has a zero in the interval [0,\pi].
    2. (b) Approximate the zero rounded to three decimal places.

  1. Intermediate Value Theorem

    1. (a) Use the Intermediate Value Theorem to show that the function f(x)=e^{x}+x-2 has a zero in the interval [0,2].
    2. (b) Approximate the zero rounded to three decimal places.

  1. (a) Since f is continuous on [0, 2], f(0) < 0 and f(2) > 0, the IVT guarantees that f must have a zero on the interval (0, 2).
  2. (b) x \approx 0.443

  1. Graph a function that is continuous on the closed interval [5,12], that is negative at both endpoints and has exactly three zeros in this interval. Does this contradict the Intermediate Value Theorem? Explain.

  1. Graph a function that is continuous on the closed interval [-1,2], that is positive at both endpoints and has exactly two zeros in this interval. Does this contradict the Intermediate Value Theorem? Explain.

This does not contradict the IVT. Answers will vary.

  1. Graph a function that is continuous on the closed interval [-2,3], is positive at -2 and negative at 3 and has exactly two zeros in this interval. Is this possible? Does this contradict the Intermediate Value Theorem? Explain.

  1. Graph a function that is continuous on the closed interval [-5,0], is negative at -5 and positive at 0 and has exactly three zeros in the interval. Is this possible? Does this contradict the Intermediate Value Theorem? Explain.

This does not contradict the IVT. Answers will vary.

    1. (a) Explain why the Intermediate Value Theorem gives no information about the zeros of the function f(x)=x^{4}-1 on the interval [-2,2].
    2. (b) Use technology to determine whether or not f has a zero on the interval [-2, 2].
    1. (a) Explain why the Intermediate Value Theorem gives no information about the zeros of the function f(x)= \ln ( x^{2}+2) on the interval [-2,2].
    2. (b) Use a graphing technology to determine whether or not f has a zero on the interval [-2, 2].

  1. (a) Answers will vary.
  2. (b) The graph below indicates that f does not have a zero in the interval (-2, 2).

  1. Intermediate Value Theorem

    1. (a) Use the Intermediate Value Theorem to show that the functions y=x^{3} and y=1-x^{2} intersect somewhere between x=0 and x=1.
    2. (b) Use graphing technology to find the coordinates of the point of intersection rounded to three decimal places.
    3. (c) Use graphing technology to graph both functions on the same set of axes. Be sure the graph shows the point of intersection.

  1. Intermediate Value Theorem An airplane is travelling at a speed of 620 miles per hour and then encounters a slight headwind that slows it to 608 miles per hour. After a few minutes, the headwind eases and the plane's speed increases to 614 miles per hour. Explain why the plane's speed is 610 miles per hour on at least two different occasions during the flight.

    Source: Submitted by the students of Millikin University.

Answers will vary.

  1. Suppose a function f is defined and continuous on the closed interval [a,b]. Is the function h(x)=\dfrac{1}{f( x) } also continuous on the closed interval [a,b]? Discuss the continuity of h on [a, b].

  1. Given the two functions f and h: \begin{equation*} {f}( x) =x^{3}-3x^{2}-4x+12\qquad h( x) =\left\{ \begin{array}{c@{\quad}l} \dfrac{f( x) }{x-3} & \hbox{if }x\neq 3 \\[5pt] p & \hbox{if }x=3 \end{array} \right. \end{equation*}

    1. (a) Find all the zeros of the function f.
    2. (b) Find the number P so that the function h is continuous at x=3. Justify your answer.
    3. (c) Determine whether h, with the number found in (b), is even, odd, or neither. Justify your answer.

  1. (a) x = -2,x = 2, x = 3
  2. (b) p = 5
  3. (c) h(x) is an even function.

  1. The function f(x)=\dfrac{|x|}{x} is not defined at 0. Explain why it is impossible to define f(0) so that f is continuous at 0.

  1. Find two functions f and g that are each continuous at c, yet \dfrac{f}{g} is not continuous at c.

Answers will vary.

  1. Discuss the difference between a discontinuity that is removable and one that is nonremovable. Give an example of each.

Bisection Method for Approximating Zeros of a Function Suppose the Intermediate Value Theorem indicates that a function f has a zero in the interval (a,b). The bisection method approximates the zero by evaluating f at the midpoint m_{1} of the interval (a, b). If f( m_{1}) =0, then m_{1} is the zero we seek and the process ends. If f( m_{1}) \neq 0, then the sign of f( m_{1}) is opposite that of either f(a) or f(b) (but not both), and the zero lies in that subinterval. Evaluate f at the midpoint m_{2} of this subinterval. Continue bisecting the subinterval containing the zero until the desired degree of accuracy is obtained.

106

In Problems 103-110, use the bisection method three times to approximate the zero of each function in the given interval.

  1. f(x) =x^{3}+3x-5; interval: (1,2)

1.1875

  1. f(x) = x^{3}-4x+2; interval: (1, 2)

  1. f(x) =2x^{3}+3x^{2}+4x-1; interval: (0,1)

0.1875

  1. f( x)=x^{3}-x^{2}-2x+1; interval: (0,1)

  1. f( x) =x^{3}-6x-12; interval: (3,4)

3.1875

  1. f( x)=3x^{3}+5x-40; interval: (2,3)

  1. f( x) =x^{4}-2x^{3}+21x-23; interval (1,2)

1.1875

  1. f( x)=x^{4}-x^{3}+x-2; interval: (1,2)

  1. Intermediate Value Theorem Use the Intermediate Value Theorem to show that the function f( x) =\sqrt{x^{2}+4x}-2 has a zero in the interval [0,1]. Then approximate the zero correct to one decimal place.

Since f is continuous on [0, 1], f(0) < 0, and f(1) > 0, the IVT guarantees that f must have a zero on the interval (0, 1). Correct to one decimal place, the zero is x = 0.8

  1. Intermediate Value Theorem Use the Intermediate Value Theorem to show that the function f(x)=x^{3}-x+2 has a zero in the interval [-2,0]. Then approximate the zero correct to two decimal places.

  1. Continuity of a Sum If f and g are each continuous at c, prove that f+g is continuous at c. [Hint: Use the Limit of a Sum Property.)

See Student Solution Manual.

  1. Intermediate Value Theorem Suppose that the functions f and g are continuous on the interval [a,b]. If f(a)\lt g(a) and f(b)>g(b), prove that the graphs of y=f(x) and y=g(x) intersect somewhere between x=a and x=b. [Hint: Define h(x) = f( x) -g(x) and show h(x) =0 for some x between a and b.]

Challenge Problems

  1. Intermediate Value Theorem Let f(x)=\dfrac{1}{x-1}+ \dfrac{1}{x-2}. Use the Intermediate Value Theorem to prove that there is a real number c between 1 and 2 for which f(c)=0.

See Student Solution Manual.

  1. Intermediate Value Theorem Prove that there is a real number c between 2.64 and 2.65 for which c^{2}=7.

  1. Show that the existence of {\lim\limits_{h\rightarrow 0}} \dfrac{f( a+h) -f( a) }{h} implies f(x) is continuous at x=a.

See Student Solution Manual.

  1. Find constants A,B,C, and D so that the function below is continuous for all x. Sketch the graph of the resulting function. \begin{equation*} f(x)=\left\{ \begin{array}{l@{\qquad}lrll} \dfrac{x^{2}+x-2}{x-1} & \hbox{if} & -\infty &\lt x\lt 1 \\ A & \hbox{if } & x&=1 \\ B\left( x-C\right) ^{2} & \hbox{if} & 1&\lt x\lt 4 \\ D & \hbox{if} & x&=4 \\ 2x-8 & \hbox{if} & 4&\lt x \lt \infty \end{array} \right. \end{equation*}

  1. Let f be a function for which 0\leq f(x)\leq 1 for all x in [0,1]. If f is continuous on [0,1], show that there exists at least one number c in [0,1] such that f(c)=c. [Hint: Let g(x)=x-f(x).]

See Student Solution Manual.