1.4 Assess Your UnderstandingPrinted Page 115
115
Concepts and Vocabulary
lim sin x = __________
0
True or False \lim\limits_{x\rightarrow 0}\dfrac{\cos x-1}{x} = 1.
False
The Squeeze Theorem states that if the functions f,g, and h have the property f(x)\leq g(x)\leq h(x) for all x in an open interval containing c, except possibly at c, and if \lim\limits_{x\rightarrow c}f(x) = \lim\limits_{x\rightarrow c}h(x) = L, then \lim\limits_{x\rightarrow c}g(x) = _________.
L
True or False f(x) = \csc x is continuous for all real numbers except x = 0.
False
Skill Building
In Problems 5-8, use the Squeeze Theorem to find each limit.
Suppose -x^{2}+1\leq g(x) \leq x^{2}+1 for all x in an open interval containing 0. Find \lim\limits_{x\rightarrow 0}g(x).
1
Suppose -(x-2) ^{2}-3\leq g(x)\leq (x-2) ^{2}-3 for all x in an open interval containing 2. Find \lim\limits_{x\rightarrow 2}g(x).
Suppose \cos x\leq g(x) \leq 1 for all x in an open interval containing 0. Find \lim\limits_{x\rightarrow 0}g(x).
1
Suppose -x^{2}+1\leq g(x) \leq \sec x for all x in an open interval containing 0. Find \lim\limits_{x\rightarrow 0}g(x).
In Problems 9-22, find each limit.
{\lim\limits_{x\rightarrow 0}}({x^{3}+\sin x})
0
{\lim\limits_{x\rightarrow 0}}({x^{2}-\cos x})
{\lim\limits_{x\rightarrow \pi /3}}({\cos x+\sin x})
\dfrac{\sqrt 3}{2} + \dfrac{1}{2}
{\lim\limits_{x\rightarrow \pi /3}}({\sin x-\cos x})
{\lim\limits_{x\rightarrow 0}}\ \dfrac{\cos x}{1+\sin x}
1
{\lim\limits_{x\rightarrow 0}}\ \dfrac{\sin x}{1+\cos x}
\lim\limits_{x\rightarrow 0}\dfrac{3}{1+e^{x}}
\dfrac{3}{2}
\lim\limits_{x \rightarrow 0}\dfrac{e^{x}-1}{1+e^{x}}
\lim\limits_{x\rightarrow 0}(e^{x}\sin x)
0
\lim\limits_{x\rightarrow 0}(e^{-x}\tan x)
\lim\limits_{x\rightarrow 1}\ln \left(\dfrac{e^{x}}{x}\right)
1
\lim\limits_{x\rightarrow 1}\ln \left(\dfrac{x}{e^{x}}\right)
\lim\limits_{x\rightarrow 0}\dfrac{e^{2x}}{1+e^{x}}
\dfrac{1}{2}
\lim\limits_{x\rightarrow 0}\dfrac{1-e^{x}}{1-e^{2x}}
In Problems 23-34, find each limit.
{\lim\limits_{x\rightarrow 0}}\dfrac{\sin (7x)}{x}
7
{\lim\limits_{x\rightarrow 0}} \dfrac{\sin \dfrac{{x}}{3}}{x}
\lim\limits_{\theta \rightarrow 0}\dfrac{\theta +3\sin \theta}{2\theta}
2
{\lim\limits_{x\rightarrow 0}}\ \dfrac{2x-5\sin (3x)}{x}
{\lim\limits_{\theta \rightarrow 0}}\ \dfrac{\sin \theta}{\theta +\tan \theta}
\dfrac{1}{2}
\lim\limits_{\theta \rightarrow 0}\dfrac{\tan \theta}{\theta}
\lim\limits_{\theta \rightarrow 0}\dfrac{5}{\theta \cdot \csc \theta}
5
\lim\limits_{\theta \rightarrow 0}\dfrac{\sin (3\theta)}{\sin (2\theta)}
\lim\limits_{\theta \rightarrow 0}\dfrac{1-\cos ^{2}\theta}{\theta}
0
\lim\limits_{\theta \rightarrow 0}\dfrac{ \cos (4\theta)-1}{2\theta}
\lim\limits_{\theta \rightarrow 0}(\theta \cdot \cot \theta)
1
\lim\limits_{\theta \rightarrow 0}\left[\sin \theta \left(\dfrac{\cot \theta -\csc \theta}{\theta}\right) \right]
In Problems 35-38, determine whether f is continuous at the number c.
f(x)=\left\{ \begin{array}{c@{\quad}l} 3\cos x & \hbox{ if } x\lt 0 \\[4pt] 3 & \hbox{ if }x=0 \\[4pt] x+3 & \hbox{ if }x>0 \end{array} \right. \quad at\quad c=0
f is continuous at c = 0.
f(x)=\left\{ \begin{array}{c@{\quad}l} \cos x & \hbox{ if }x\lt 0 \\[4pt] 0 & \hbox{ if }x=0 \\[4pt] e^{x} & \hbox{ if }x\gt 0 \end{array} \right. \quad at\quad c=0
f(\theta )=\left\{ \begin{array}{l@{\quad}l} \sin \theta & \hbox{ if }\theta \leq\dfrac{\pi }{4} \\[8pt] \cos \theta & \hbox{ if }\theta >\dfrac{\pi }{4} \end{array} \right. at\quad c=\dfrac{\pi }{4}
f is continuous at c=\dfrac{\pi}{4}.
f(x)=\left\{ \begin{array}{c@{\quad}l} \tan ^{-1}x & \hbox{ if }x\lt 1 \\[4pt] \ln x & \hbox{ if }x\geq 1 \end{array} \right. at\quad c=1
In Problems 39-46, determine where f is continuous.
f(x) = \sin \left(\dfrac{x^{2}-4x}{x-4}\right)
f is continuous on {\{} x \vert x \ne 4 {\}}.
f(x) = \cos \left(\dfrac{x^{2}-5x+1}{2x}\right)
f(\theta) = \dfrac{1}{1+\sin \theta}
f is continuous on \left\{ x \vert x \ne \dfrac{3\pi }{2} + 2k\pi \right\}, k an integer.
f(\theta) = \dfrac{1}{1+\cos^{2}\theta}
f(x) = \dfrac{\ln x}{x-3}
f is continuous on {\{} x \vert x > 0, x \ne 3 {\}}.
f(x) = \ln (x^{2}+1)
f(x) = e^{-x}\sin x
f is continuous on the set of all real numbers.
f(x) = \dfrac{e^{x}}{1+\sin ^{2}x}
Applications and Extensions
In Problems 47-50, use the Squeeze Theorem to find each limit.
\lim\limits_{x\rightarrow 0}\left(x^{2}\sin \dfrac{1}{x}\right)
0
\lim\limits_{x\rightarrow 0}\left[ x\left(1-\cos \dfrac{1}{x}\right) \right]
\lim\limits_{x\rightarrow 0}\left[ x^{2}\left(1-\cos \dfrac{1}{x}\right) \right]
0
\lim\limits_{x\rightarrow 0}\left[ \sqrt{x^{3}+3x^{2}}\sin \left(\dfrac{1}{x}\right) \right]
In Problems 51-54, show that each statement is true.
\lim\limits_{x\rightarrow 0}\dfrac{\sin (ax)}{\sin (bx)} = \dfrac{a}{b}; b\neq0
See Student Solution Manual.
\lim\limits_{x\rightarrow 0}\dfrac{\cos (ax)}{\cos (bx)} = 1\qquad
\lim\limits_{x\rightarrow 0}\dfrac{\sin (ax)}{bx} = \dfrac{a}{b}; b\neq 0
See Student Solution Manual.
\lim\limits_{x\rightarrow 0}\dfrac{1-\cos (ax)}{bx} = 0 a\neq 0, b\neq 0
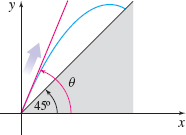
Projectile Motion An object is propelled from ground level at an angle \theta , \dfrac{\pi}{4}\lt \theta \lt \dfrac{\pi}{2}, up a ramp that is inclined to the horizontal at an angle of 45^{\circ}. See the figure. If the object has an initial velocity of 10 feet/second, the equations of the horizontal position x = x(\theta) and the vertical position y = y(\theta) of the object after t seconds are given by \begin{equation*} x = x(\theta) = (10\cos \theta) t \quad \hbox{and} \quad y = y(\theta) = -16t^{2}+ (10\sin \theta) t \end{equation*}
116
For t fixed,
- (a) Find \lim\limits_{\theta \rightarrow {\pi}/{4}^{+}}x(\theta) and \lim\limits_{\theta \rightarrow {\pi}/{4} ^{+}}y (\theta).
- (b) Are the limits found in (a) consistent with what is expected physically?
- (c) Find \lim\limits_{\theta \rightarrow {\pi}/{2}^{-}}x(\theta) and \lim\limits_{\theta \rightarrow {\pi}/{2}^{-}}y(\theta).
- (d) Are the limits found in (c) consistent with what is expected physically?
- (a) \mathop {\lim\limits_{\theta \to {\pi}/{4}^ + }} x(\theta ) = 5\sqrt 2 t, \mathop {\lim\limits_{\theta \to {\pi}/{4}^ + }} y(\theta ) = - 16t^2 + 5\sqrt 2 t
- (b) Answers will vary.
- (c) \mathop {\lim\limits_{\theta \to {\pi}/{2}^ - }} x(\theta ) = 0, \mathop {\lim\limits_{\theta \to {\pi}/{2}^ + }} y(\theta ) = - 16t^2 + 10t
- (d) Answers will vary.
Show that \lim\limits_{x\rightarrow 0}\dfrac{1-\cos x}{ x^{2}} = \dfrac{1}{2}.
Squeeze Theorem If 0\leq f(x)\leq 1 for every number x, show that \lim\limits_{x\rightarrow 0}[ x^{2}f(x)] = 0.
See Student Solution Manual.
Squeeze Theorem If 0\leq f(x)\leq M for every x, show that \lim\limits_{x\rightarrow 0}[ x^{2}f(x)] = 0.
The function f(x) = \dfrac{\sin (\pi x)}{x} is not defined at 0. Decide how to define f(0) so that f is continuous at 0.
f(0) = \pi
Define f(0) and f(1) so that the function f(x) = \dfrac{\sin (\pi x)}{x(1-x)} is continuous on the interval $[0,1]\).
Is f(x)=\left\{ \begin{array}{c@{\quad}l} \dfrac{\sin x}{x} & \hbox{if }x\neq 0 \\[10pt] 1 & \hbox{if }x=0 \end{array} \right. continuous at 0?
Yes
Is f(x) = {\left\{ \begin{array}{c@{\quad}l} \dfrac{1-\cos x}{x} & \hbox{if }x\neq 0 \\[10pt] 0 & \hbox{if }x = 0 \end{array} \right.} continuous at 0?
Squeeze Theorem Show that \lim\limits_{x\rightarrow0}\left[x^{n}\sin \left(\dfrac{1}{x}\right) \right] = 0, where n is a positive integer. (Hint: Look first at Problem 57.)
See Student Solution Manual.
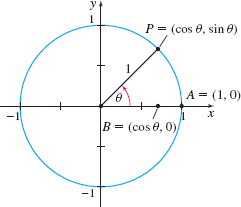
Prove \lim\limits_{\theta \rightarrow 0}\sin \theta = 0. (Hint: Use a unit circle as shown in the figure, first assuming 0\lt \theta \,\lt \dfrac{\pi}{2}. Then use the fact that \sin \theta is less than the length of the arc AP, and the Squeeze Theorem, to show that \lim\limits_{\theta \rightarrow 0^{+}}\sin \theta = 0. Then use a similar argument with -\dfrac{\pi}{2}\lt \theta \lt 0 to show \lim\limits_{\theta \rightarrow 0^{-}}\sin \theta = 0.)
Prove \lim\limits_{\theta \rightarrow 0}\cos \theta = 1. Use either the proof outlined in Problem 64 or a proof using the result \lim\limits_{\theta \rightarrow 0}\sin \theta = 0 and a Pythagorean identity.
See Student Solution Manual.
Without using limits, explain how you can decide whether f(x) = \cos (5x^{3}+2x^{2}-8x+1) is continuous.
Explain the Squeeze Theorem. Draw a graph to illustrate your explanation.
Answers will vary.
Challenge Problems
Use the Sum Formulas \sin (a+b) = \sin a\cos b+\cos a\sin b and \cos (a+b) = \cos a\cos b-\sin a\sin b to show that the sine function and cosine function are continuous on their domains.
Find \lim\limits_{x\rightarrow 0}\dfrac{\sin x^{2}}{x}.
0
Squeeze Theorem If f(x)=\left\{ \begin{array}{l@{\quad}l} 1 & \hbox{if }x\hbox{ is rational} \\[3pt] 0 & \hbox{if }x\hbox{ is irrational} \end{array} \right. show that \lim\limits_{x\rightarrow 0}[ xf(x)] =0.
Suppose points A and B with coordinates (0,0) and (1,0), respectively, are given. Let n be a number greater than 0, and let \theta be an angle with the property 0\lt \theta \lt \dfrac{\pi}{1+n}. Construct a triangle ABC where \overline{AC} and \overline{AB} form the angle \theta , and \overline{CB} and \overline{AB} form the angle n\,\theta (see the figure below). Let D be the point of intersection of \overline{AB} with the perpendicular from C to \overline{AB}. What is the limiting position of D as \theta approaches 0?
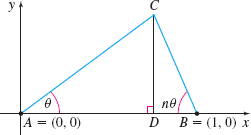
\left(\dfrac{n}{n + 1}, 0\right)
