TABLE OF INTEGRALS
General Formulas
1.
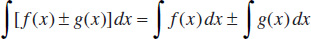
2.
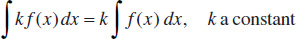
3.
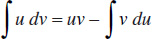
Essential Integrals
1.
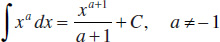
2.
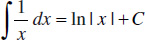
3.
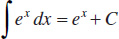
4.
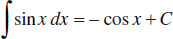
5.
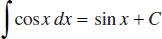
6.
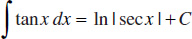
7.
8.
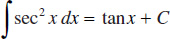
9.
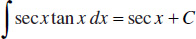
10.
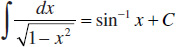
11.
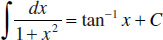
12.
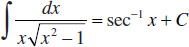
13.
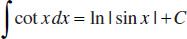
14.
15.
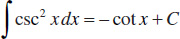
16.
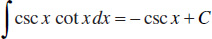
17.
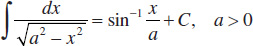
18.
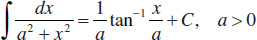
19.
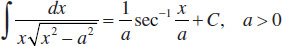
20.
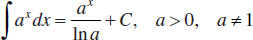
Useful Integrals
21.
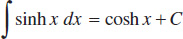
22.
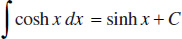
23.
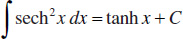
24.
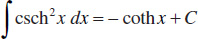
25.
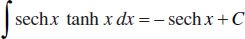
26.
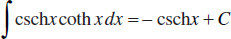
27.
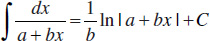
28.
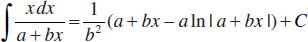
29.
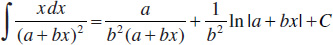
30.
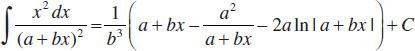
31.
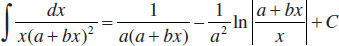
32.
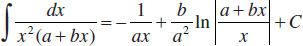
33.
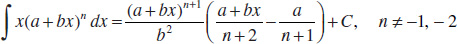
34.
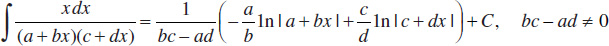
35.
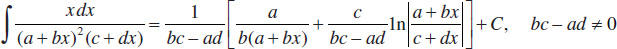
36.
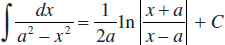
37.
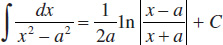
38.
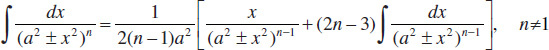
39.
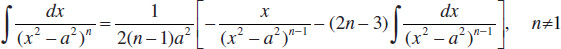
Integrals Containing \(\sqrt{a+bx}\)
40.
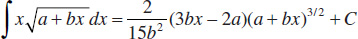
41.
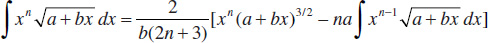
42.
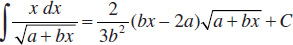
43.
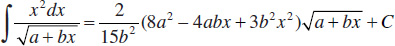
44.
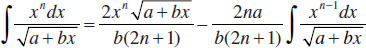
45.
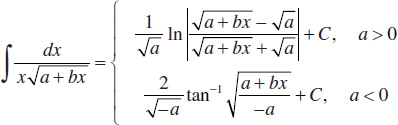
46.
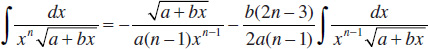
47.
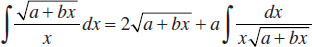
48.
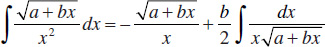
Integrals Containing \(\sqrt{x^{2}{\ }{\pm}{\ }a^{2}}\)
49.
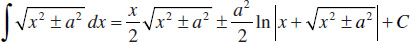
50.
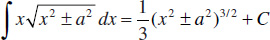
51.
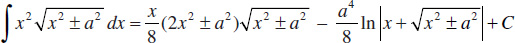
52.
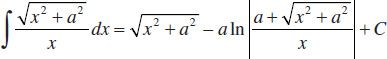
53.
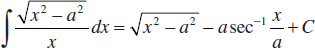
54.
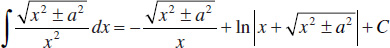
55.
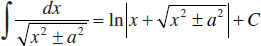
56.
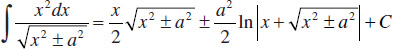
57.
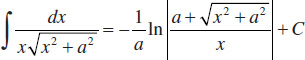
58.
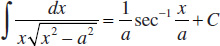
59.
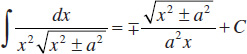
60.
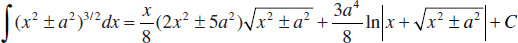
61.
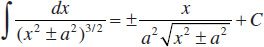
Integrals Containing \(\sqrt{a^{2}{\ }-{\ }x^{2}}\)
62.
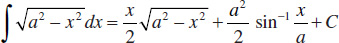
63.
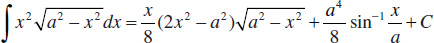
64.
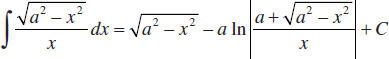
65.
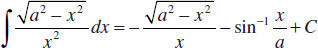
66.
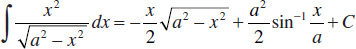
67.
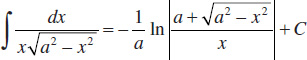
68.
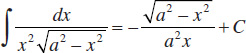
69.
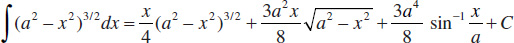
70.
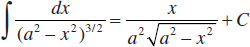
Integrals Containing \(\sqrt{2ax{\ }-{\ }x^{2}}\)
71.
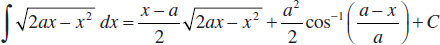
72.
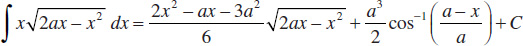
73.
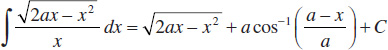
74.
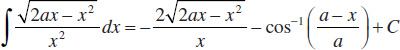
75.
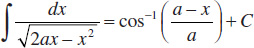
76.
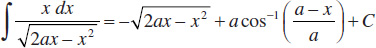
77.
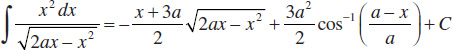
78.
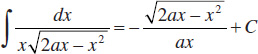
79.
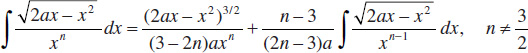
80.
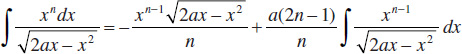
81.
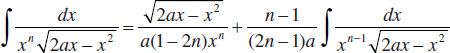
82.
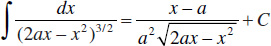
83.
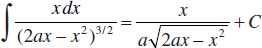
Integrals Containing Trigonometric Functions
84. \(\int \sin^2 x dx = \dfrac{x}{2} - \dfrac{\sin (2x)}{4} + C\)
85. \(\int \cos^2 x dx = \dfrac{x}{2} + \dfrac{\sin (2x)}{4} + C\)
86.
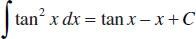
87.
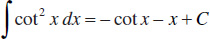
88.
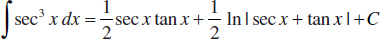
89.
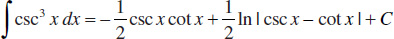
90.
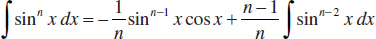
91.
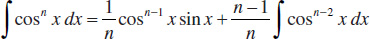
92.
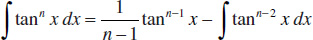
93.
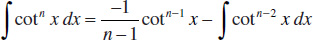
94.
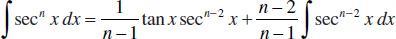
95.
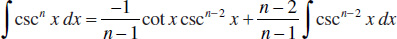
96. \(\int \sin (mx) \sin (nx) dx = -\dfrac{\sin[(m + n) x]}{2(m + n)} + \dfrac{\sin[(m - n)x]}{2(m - n)} + C, m^2 \neq n^2 \)
97. \(\int \cos (mx) \cos (nx) dx = \dfrac{\sin[(m + n) x]}{2(m + n)} + \dfrac{\sin[(m - n)x]}{2(m - n)} + C, m^2 \neq n^2 \)
98. \(\int \sin (mx) \cos (nx) dx = -\dfrac{\cos[(m + n) x]}{2(m + n)} - \dfrac{\cos[(m - n)x]}{2(m - n)} + C, m^2 \neq n^2 \)
99.
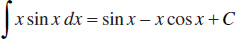
100.
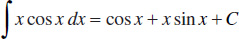
101.
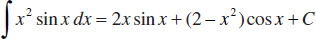
102.
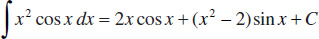
103.
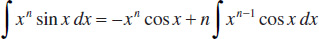
104.
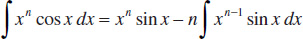
105.
(a)
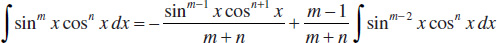
(b)
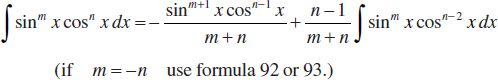
Integrals Containing Inverse Trigonometric Functions
106.
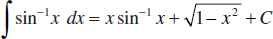
107.
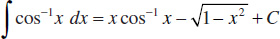
108.
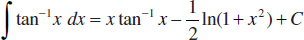
109.
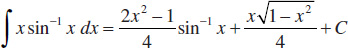
110.
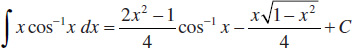
111.
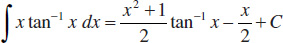
112.
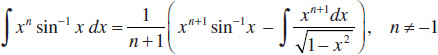
113.
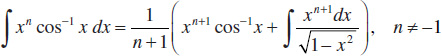
114.
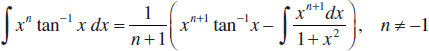
Integrals Containing Exponential and Logarithmic Functions
115.
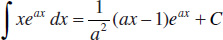
116.
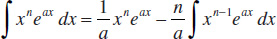
117.
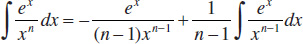
118.
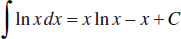
119.
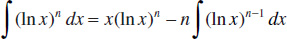
120.
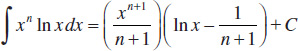
121.
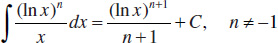
122.
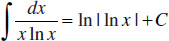
123.
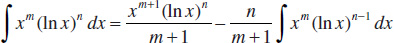
124.
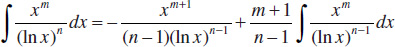
125.
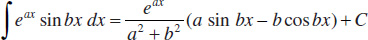
126.
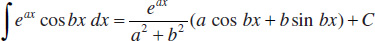
Integrals Containing Hyperbolic Functions
127.
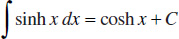
128.
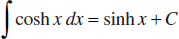
129.
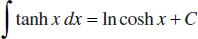
130.
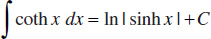
131.
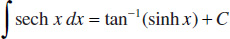
132.
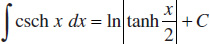
133.
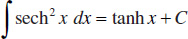
134.
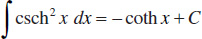
135.
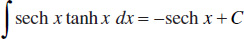
136.
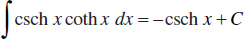
137.
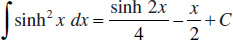
138.
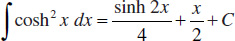
139.
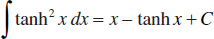
140.
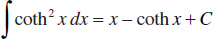
141.
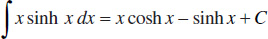
142.
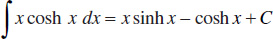
143.
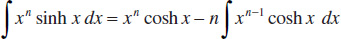
144.
