2.1 Assess Your UnderstandingPrinted Page 151
Concepts and Vocabulary
True or False The derivative is used to find instantaneous velocity.
True
True or False The derivative can be used to find the rate of change of a function.
True
The notation f′(c) is read f ______ of c; f′(c) represents the ______ of the tangent line to the graph of f at the point ______.
Prime, slope, (c,f(c))
True or False If it exists, lim is the derivative of the function f at 3.
True
If f( x) =x^{2}-3, then f^\prime (3) =______.
6
Velocity, the slope of a tangent line, and the rate of change of a function are three different interpretations of the mathematical concept called the ______.
derivative
Skill Building
Approximating Velocity An object in rectilinear motion moves according to the equation s=10t^{2} (s in centimeters). Approximate the velocity of the object at time t_{0}=3 seconds by letting \Delta t first equal 0.1 second, then 0.01 second, and finally 0.001 second. What limit does the velocity appear to be approaching? Organize the results in a table.
| Time interval | \Delta t | \dfrac{\Delta s}{\Delta t} |
|---|---|---|
| [3,3.1] | 0.1 | 61 |
| [3,3.01] | 0.01 | 60.1 |
| [3,3.001] | 0.001 | 60.01 |
The velocity appears to approach 60 cm/s.
Approximating Velocity An object in rectilinear motion moves according to the equation s=5-t^{2} (s in centimeters and t in seconds). Approximate the velocity of the object at time t_{0}=1 by letting \Delta t first equal 0.1, then 0.01, and finally 0.001. What limit does the velocity appear to be approaching? Organize the results in a table.
Rectilinear Motion As an object in rectilinear motion moves, the distance s (in meters) that it moves in t_{0} seconds is given by s=f(t)=3t^{2}+4t. Find the velocity v at t_{0}=0. At t_{0}=2. At any time t_{0}.
v(t)=4 m/s at t=0, v(t)=16 m/s at t=2, v(t)=6t_0+4 m/s at any t_0
Rectilinear Motion As an object in rectilinear motion moves, the distance s (in meters) that it moves in t seconds is given by s=f(t)=2t^{3}+4. Find the velocity v at t_{0}=0. At t_{0}=3. At any time t_{0}.
Rectilinear Motion As an object in rectilinear motion moves, its distance s from the origin at time t is given by the equation s=s( t) =3t^{2}-\dfrac{1}{t}, where s is in centimeters and t is in seconds. Find the velocity v of the object at t_{0}=1 and t_{0}=4.
v(1)=7 cm/s, v(4)=\dfrac{385}{16} cm/s
Rectilinear Motion As an object in rectilinear motion moves, its distance s from the origin at time t is given by the equation s=s( t) =\sqrt{4t}, where s is in centimeters and t is in seconds. Find the velocity v of the object at t_{0}=1 and t_{0}=4.
152
In Problems 13-22, find an equation of the tangent line to the graph of each function at the indicated point. Graph each function and the tangent line.
f(x)=3x^{2} at (-2,12)
y=-12x-12

f(x)=x^{2}+2 at (-1,3)
f(x)=x^{3} at (-2,-8)
y=12x+16

f(x)=x^{3}+1 at (1,2)
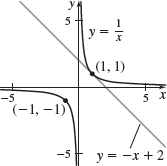
f(x)={\dfrac{1}{x}} at (1,1)
y=-x+2
f(x)=\sqrt{x} at (4,2)
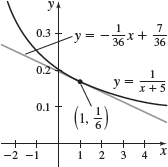
{f(x)=\dfrac{1}{x+5}} at {\left(1,\dfrac{1}{6}\right) }
y=-\dfrac{1}{36}x+\dfrac{7}{36}
{f(x)=\dfrac{2}{x+4}} at {\left(1,\dfrac{2}{5}\right) }
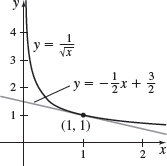
{f(x)=\dfrac{1}{\sqrt{x}},} at {(1,1)}
y=-\dfrac{1}{2}x+\dfrac{3}{2}
f(x)=\dfrac{1}{x^2} at {(1,1)}
In Problems 23-26, find the rate of change of f at the indicated numbers.
f(x)=5x-2 at (a) c=0, (b) c=2, (c) c any real number
- (a) 5
- (b) 5
- (c) 5
f(x)=x^{2}-1 at (a) c=-1, (b) c=1, (c) c any real number
{f(x)=\dfrac{x^{2}}{x+3}} at (a) c=0, (b) c=1, (c) c any real number, c\neq -3
- (a) 0
- (b) \dfrac{7}{16}
- (c) \dfrac{c(c+6)}{(c+3)^{2}}
{f(x)=\dfrac{x}{x^{2}-1}} at (a) c=0, (b) c=2, (c) c any real number, c\neq \pm 1
In Problems 27-36, find the derivative of each function at the given number.
f(x)=2x+3 at 1
f'(1)=2
f(x)=3x-5 at 2
f(x)=x^{2}-2 at 0
f'(0)=0
f(x)=2x^{2}+4 at 1
f(x)=3x^{2}+x+5 at -1
f'(-1)=-5
f(x)=2x^{2}-x-7 at -1
f(x)=\sqrt{x} at 4
f'(4)=\dfrac{1}{4}
f(x)={\dfrac{1}{x^{2}}} at 2
{f(x)=\dfrac{2-5x}{1+x}} at 0
f'(0)=-7
{f(x)=\dfrac{2+3x}{2+x}} at 1
The Princeton Dinky is the shortest rail line in the country. It runs for 2.7 miles, connecting Princeton University to the Princeton Junction railroad station. The Dinky starts from the university and moves north toward Princeton Junction. Its distance from Princeton is shown in the graph where the time t is in minutes and the distance s of the Dinky from Princeton University is in miles.

- (a) When is the Dinky headed toward Princeton University?
- (b) When is it headed toward Princeton Junction?
- (c) When is the Dinky stopped?
- (d) Find its average speed on a trip from Princeton to Princeton Junction.
- (e) Find its average speed for the round trip shown in the graph, that is, from t=0 to t=13.

- (a) 7\leq t\leq 10 and 11\leq t\leq 13
- (b) 0\leq t\leq 4
- (c) 4 \le t \le 7 and 10 \le t\le 11
- (d) Average speed \approx 0.675 mi/min
- (e) 0.415 mi/min
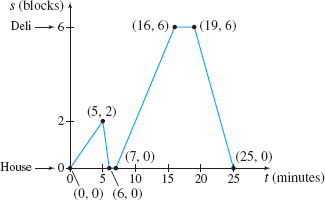
Barbara walks to the deli, which is six blocks east of her house. After walking two blocks, she realizes she left her phone on her desk, so she runs home. After getting the phone, closing and locking the door, Barbara starts on her way again. At the deli, she waits in line to buy a bottle of vitaminwater^{\rm TM}, and then she jogs home. The graph below represents Barbara’s journey. The time t is in minutes and s is Barbara’s distance, in blocks, from home.
- (a) At what times is she headed toward the deli?
- (b) At what times is she headed home?
- (c) When is the graph horizontal? What does this indicate?
- (d) Find Barbara’s average speed from home until she starts back to get her phone.
- (e) Find Barbara’s average speed from home to the deli after getting her phone.
- (f) Find her average speed from the deli to home.
Applications and Extensions
Slope of a Tangent Line The equation of the tangent line to the graph of a function f at (2,6) is y=-3x+12. What is f^\prime (2)?
-3
Slope of a Tangent Line The equation of the tangent line of a function f at (3,2) is y=\dfrac{1}{3}x+1. What is f^\prime (3)?
Tangent Line Does the tangent line to the graph of y=x^{2} at (1, 1) pass through the point (2, 5)?
No
153
Tangent Line Does the tangent line to the graph of y=x^{3} at (1,1) pass through the point (2,5)?
Respiration Rate A human being’s respiration rate R (in breaths per minute) is given by R=R\left( p\right) = 10.35+0.59p, where p is the partial pressure of carbon dioxide in the lungs. Find the rate of change in respiration when p=50.
R'(50)=0.59
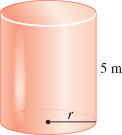
Instantaneous Rate of Change The volume V of the right circular cylinder of height 5m and radius rm shown in the figure is V=V( r) =5\pi r^{2}. Find the instantaneous rate of change of the volume with respect to the radius when r=3{m}.
Market Share During a month-long advertising campaign, the total sales S of a magazine is modeled by the function S(x) =5x^{2}+100x+10{,}000, where x represents the number of days since the campaign began, 0 ≤ x ≤ 30.
- (a) What is the average rate of change of sales from x=10 to x=20 days?
- (b) What is the instantaneous rate of change of sales when x=10 days?
- (a) 250 sales per day
- (b) 200 sales per day
Demand Equation The demand equation for an item is p=p( x) =90-0.02x, where p is the price in dollars and x is the number of units (in thousands) made.
- (a) Assuming all units made can be sold, find the revenue function R( x) =xp( x).
- (b) Marginal Revenue Marginal revenue is defined as the additional revenue earned by selling an additional unit. If we use R^\prime (x) to measure the marginal revenue, find the marginal revenue when 1 million units are sold.
Gravity If a ball is dropped from the top of the Empire State Building, 1002 ft above the ground, the distance s (in feet) it falls after t seconds is s(t)=16t^{2}.
- (a) What is the average velocity of the ball for the first 2s?
- (b) How long does it take for the ball to hit the ground?
- (c) What is the average velocity of the ball during the time it is falling?
- (d) What is the velocity of the ball when it hits the ground?
- (a) 32 ft/s
- (b) t\approx 7.914\ {\rm s}
- (c) Average velocity \approx 126.618\ {\rm ft}/{\rm s}
- (d) v(7.914)\approx 253.235 ft/s
Velocity A ball is thrown upward. Its height h in feet is given by h(t)=100t-16t^{2}, where t is the time elapsed in seconds.
- (a) What is the velocity v of the ball at t=0{s}, t=1{s}, and t=4{s}?
- (b) At what time t does the ball strike the ground?
- (c) At what time t does the ball reach its highest point? (Hint: At the time the ball reaches its maximum height, it is stationary. So, its velocity v= 0.)
Gravity A rock is dropped from a height of 88.2 m and falls toward Earth in a straight line. In t seconds the rock falls 4.9t^{2} meters.
- (a) What is the average velocity of the rock for the first 2s?
- (b) How long does it take for the rock to hit the ground?
- (c) What is the average velocity of the rock during its fall?
- (d) What is the velocity v of the rock when it hits the ground?
- (a) 9.8 {\rm m}/{\rm s}
- (b) t\approx 4.243\ {\rm s}
- (c) Average velocity \approx 20.789\ {\rm m}/{\rm s}
- (d) v(4.243)\approx 41.578 m/s
Velocity At a certain instant, the speedometer of an automobile reads V mi/h. During the next \dfrac{1}{4} s the automobile travels 20 ft. Estimate V from this information.
Volume of a Cube A metal cube with each edge of length x centimeters is expanding uniformly as a consequence of being heated.
- (a) Find the average rate of change of the volume of the cube with respect to an edge as x increases from 2.00 to 2.01cm.
- (b) Find the instantaneous rate of change of the volume of the cube with respect to an edge at the instant when x=2{cm}.
- (a) \dfrac{\Delta V}{\Delta x}\approx 12.060\ {\rm cm}^{3}/{\rm cm}
- (b) V'(2)=12\ {\rm cm}^{3}/{\rm cm}
Rate of Change Show that the rate of change of a linear function f( x) =mx+b is the slope m of the line y=mx+b.
Rate of Change Show that the rate of change of a quadratic function f( x) =ax^{2}+bx+c is a linear function of x.
f'(x)=2ax+b
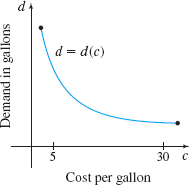
Business The graph represents the demand d (in gallons) for olive oil as a function of the cost c in dollars per gallon of the oil.
- (a) Interpret the derivative d^\prime (c).
- (b) Which is larger, d^\prime ( 5) or d^\prime (30)? Give an interpretation to d^\prime (5) and d^\prime (30).
Agriculture The graph represents the diameter d (in centimeters) of a maturing peach as a function of the time t (in days) it is on the tree.
- (a) Interpret the derivative d^\prime (t) as a rate of change.
- (b) Which is larger, d^\prime (1) or d^\prime (20)?
- (c) Interpret both d^\prime (1) and d^\prime (20).
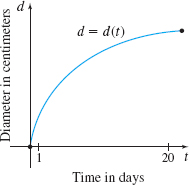
- (a) d'(t) is the rate of change of diameter (in centimeters) with respect to time (in days).
- (b) d'(1)>d'(20)
- (c) d'(1) is the instantaneous rate of change of the peach's diameter on day 1 and d'(20) is the instantaneous rate of change of the peach's diameter on day 20.
