3.1 Assess Your UnderstandingPrinted Page 205
Concepts and Vocabulary
The derivative of a composite function (f∘g)(x) can be found using the ______ Rule.
Chain
True or False If y=f(u) and u=g(x) are differentiable functions, then y=f(g(x)) is differentiable.
True
True or False If y=f(g(x)) is a differentiable function, then y′= f′(g′(x)).
False
To find the derivative of y=tan(1+cosx), using the Chain Rule, begin with y = ______ and u = ______.
tanu; 1+cosx
If y=(x3+4x+1)100, then y′= ______.
100(x3+4x+1)99(3x2+4)
If f(x)=e3x2+5, then f′(x)= ______.
6xe3x2+5
True or False The Chain Rule can be applied to multiple composite functions.
True
ddxsinx2= ______.
2xcos(x2)
Skill Building
In Problems 9–14, write y as a function of x. Find dydx using the Chain Rule.
y=u5, u=x3+1
y = (x3 + 1)5; dydx=15x2(x3+1)4
y=u3, u=2x+5
y=uu+1, u=x2+1
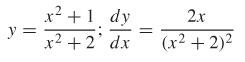
y=u−1u, u=x2−1
y=(u+1)2, u=1x

y=(u2−1)3, u=1x+2
In Problems 15–32, find the derivative of each function using the Power Rule for Functions.
f(x)=(3x+5)2
f′(x)=6(3x+5)
f(x)=(2x−5)3
f(x)=(6x−5)−3
f′(x)=−18(6x−5)4
f(t)=(4t+1)−2
g(x)=(x2+5)4
g′(x)=8x(x2+5)3
F(x)=(x3−2)5
f(u)=(u−1u)3
f′(u)=3(u−1u)2(1+1u2)
f(x)=(x+1x)3
g(x)=(4x+ex)3
g′(x)=3(4x+ex)2(4+ex)
F(x)=(ex−x2)2
f(x)=tan2x
f′(x)=2tanxsec2x
f(x)=sec3x
f(z)=(tanz+cosz)2
f′(z)=2(tanz+cosz)(sec2z−sinz)
f(z)=(ez+2sinz)3
y=(x2+4)2(2x3−1)3
y′=4x(x2+4)(2x3−1)3+18x2(x2+4)2(2x3−1)2=2x(x2+4)(2x3−1)2(13x3+36x−2)
y=(x2−2)3(3x4+1)2
y=(sinxx)2
y′=2sinx(xcosx−sinx)x3
y=(x+cosxx)5
206
In Problems 33–54, find y′.
y=sin(4x)
y′=4cos(4x)
y=cos(5x)
y=2sin(x2+2x−1)
y′=2cos(x2+2x−1)⋅(2x+2)
y=12cos(x3−2x+5)
y=sin1x
y′=cos1x⋅(−1x2)
y=sin3x
y=sec(4x)
y′=4sec(4x)tan(4x)
y=cot(5x)
y=e1/x
y′=e1/x(−1x2)
y=e1/x2
y=1x4−2x+1
y′=−4x3−2(x4−2x+1)2
y=3x5+2x2−3
y=1001+99e−x
y′=9900e−x(1+99e−x)2
y=11+2e−x
y=2sinx
y′=(ln2)2sinxcosx
y=(√3)cosx
y=6secx
y′=(ln6)6secxsecxtanx
y=3tanx
y=5xe3x
y′=5e3x+15xe3x
y=x3e2x
y=x2sin(4x)
y′=2xsin(4x)+4x2cos(4x)
y=x2cos(4x)
In Problems 55–58, find y′ (a and b are constants).
y=e−axsin(bx)
y′=−ae−axsin(bx)+be−axcos(bx)
y=eaxcos(−bx)
y=eax−1eax+1
y′=2aeax(eax+1)2
y=e−ax+1ebx−1
In Problems 59–62, write y as a function of x. Find dydx using the Chain Rule.
y=u3, u=3v2+1, v=4x2
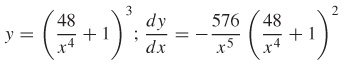
y=3u, u=3v2−4, v=1x
y=u2+1, u=4v, v=x2
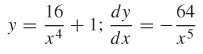
y=u3−1, u=−2v, v=x3
In Problems 63–70, find y′.
y=e−2xcos(3x)
y′=−2e−2xcos(3x)−3e−2xsin(3x)
y=eπxtan(πx)
y=cos(ex2)
y′=−2xex2sin(ex2)
y=tan(ex2)
y=ecos(4x)
y′=ecos(4x)(−4sin(4x))
y=ecsc2x
y=4sin2(3x)
y′=24sin(3x)cos(3x)
y=2cos2(x2)
In Problems 71 and 72, find the derivative of each function by:
- (a) Using the Chain Rule.
- (b) Using the Power Rule for Functions.
- (c) Expanding and then differentiating.
- (d) Verify the answers from parts (a)–(c) are equal.
y=(x3+1)2
- (a) y′=6x2(x3+1)
- (b) y′=6x2(x3+1)
- (c) y′=6x5+6x2
y=(x2−2)3
In Problems 73–78:
- (a) Find an equation of the tangent line to the graph of f at the given point.
- (b)
 Use graphing technology to graph f and the tangent line on the same screen.
Use graphing technology to graph f and the tangent line on the same screen.
f(x)=(x2−2x+1)5 at (1,0)
- (a) y=0
- (b)

f(x)=(x3−x2+x−1)10 at (0,1)
f(x)=x(x2−1)3 at (2,227)
- (a) y=1627−7x27
- (b)
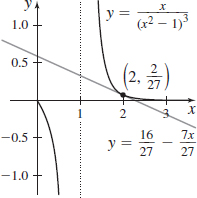
f(x)=x2(x2−1)2 at (2,49)
f(x)=sin(2x)+cosx2 at (0,1)
- (a) y=2x+1
- (b)
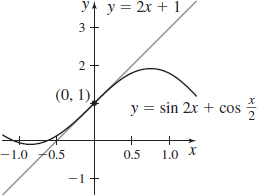
f(x)=sin2x+cos3x at (π2,1)
In Problems 79 and 80, find the indicated derivative.
d2dx2cos(x5)
d2ydx2=−25x8cos(x5)−20x3sin(x5)
d3dx3sin3x
Suppose h=f∘g. Find h′(1) if f′(2)=6, f(1)=4, g(1)=2, and g′(1)=−2.
h′(1)=−12
Suppose h=f∘g. Find h′(1) if f′(3)=4, f(1)=1, g(1)=3, and g′(1)=3.
Suppose h=g∘f. Find h′(0) if f(0)=3, f′(0)=−1, g(3)=8, and g′(3)=0.
h′(0)=0
Suppose h=g∘f. Find h′(2) if f(1)=2, f′(1)=4, f(2)=−3, f′(2)=4, g(−3)=1, and g′(−3)=3.
If y=u5+u and u=4x3+x−4, find dydx at x=1.
78
If y=eu+3u and u=cosx, find dydx at x=0.
Applications and Extensions
In Problems 87–94, find the indicated derivative.
ddxf(x2+1) (Hint: Let u=x2+1.)
dfdx=f′(x2+1)(2x)
ddxf(1−x2)
ddxf(x+1x−1)
dfdx=f′(x+1x−1)(−2(x−1)2)
ddxf(1−x1+x)
ddxf(sinx)
dfdx=f′(sinx)cosx
ddxf(tanx)
d2dx2f(cosx)
d2fdx2=f″
\dfrac{d^{2}}{dx^{2}} f(e^{x})
Rectilinear Motion The distance s, in meters, of an object from the origin at time t ≥ 0 seconds is given by s=s( t) = A\cos (\omega t+\phi ), where A, \omega , and \phi are constant.
- (a) Find the velocity v of the object at time t.
- (b) When is the velocity of the object 0?
- (c) Find the acceleration a of the object at time t.
- (d) When is the acceleration of the object 0?
(a) 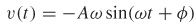
(b) 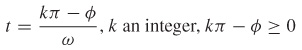
(c) 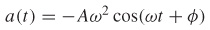
(d) 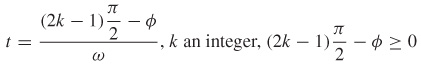
Rectilinear Motion A bullet is fired horizontally into a bale of paper. The distance s (in meters) the bullet travels into the bale of paper in t seconds is given by s=s( t) =8-(2-t)^{3},\quad 0 ≤ t≤ 2.
- (a) Find the velocity v of the bullet at any time t.
- (b) Find the velocity of the bullet at t= 1 and at t=2.
207
- (c) Find the acceleration a of the bullet at any time t.
- (d) Find the acceleration of the bullet at t=1 and at t=2.
- (e) How far into the bale of paper did the bullet travel?
Rectilinear Motion Find the acceleration a of a car if the distance s, in feet, it has traveled along a highway at time t≥ 0 seconds is given by s( t) =\frac{80}{3}\left[ {{t+\frac{3}{\pi }\sin }}\left( {{\frac{\pi }{6}t}}\right) \right]
- (a) a(t)={-20\pi\over 9}\sin \dfrac{\pi t}{6}
Rectilinear Motion An object moves in rectilinear motion so that at time t≥ 0 seconds, its distance from the origin is s(t) =\sin e^{t}, in feet.
- (a) Find the velocity v and acceleration a of the object at any time t.
- (b) At what time does the object first have zero velocity?
- (c) What is the acceleration of the object at the time t found in (b)?
Resistance The resistance R (measured in ohms) of an 80-meter-long electric wire of radius x (in centimeters) is given by the formula R=R(x) =\dfrac{0.0048}{x^{2}}. The radius x is given by x=0.1991 + 0.000003T where T is the temperature in Kelvin. How fast is R changing with respect to T when T=320{\,{\rm{K}}}?
{dR\over dT} = -3.597\times 10^{-6} ohms/K
Pendulum Motion in a Car The motion of a pendulum swinging in the direction of motion of a car moving at a low, constant speed, can be modeled by s=s(t)=0.05\sin (2t)+3t \ \ \ \ \ \ 0≤ t≤ \pi where s is the distance in meters and t is the time in seconds.
- (a) Find the velocity v at t=0, t=\dfrac{\pi }{8}, t=\dfrac{\pi }{4}, t=\dfrac{\pi }{2}, and t=\pi .
- (b) Find the acceleration a at the times given in (a).
- (c)
 Graph s=s(t), v=v(t), and a=a(t) on the same screen.
Graph s=s(t), v=v(t), and a=a(t) on the same screen.
Source: Mathematics students at Trine University.
Economics The function A(t) =102-90\,e^{-0.21t} represents the relationship between A, the percentage of the market penetrated by second-generation smart phones, and t, the time in years, where t=0 corresponds to the year 2010.
- (a) Find \lim\limits_{t\rightarrow \infty}A(t) and interpret the result.
- (b)
 Graph the function A=A( t) , and explain how the graph supports the answer in (a).
Graph the function A=A( t) , and explain how the graph supports the answer in (a). - (c) Find the rate of change of A with respect to time.
- (d) Evaluate A^\prime (5) and A^\prime (10) and\ interpret these results.
- (e)
 Graph the function A^\prime =A^\prime ( t) , and explain how the graph supports the answers in (d).
Graph the function A^\prime =A^\prime ( t) , and explain how the graph supports the answers in (d).
- (a) 102
- (b)
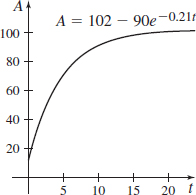
- (c) {dA\over dt}=18.9 e^{-0.21 t}
- (d) A'(5)=6.614 \mathsf{\small \%/yr}; A'(10)=2.314 \mathsf{\small \%/yr}
- (e)
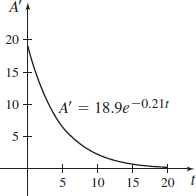
Meteorology The atmospheric pressure at a height of x meters above sea level is P(x)=10^{4}e^{-0.00012x} kilograms per square meter. What is the rate of change of the pressure with respect to the height at x=500 m? At x=750 m?
Hailstones Hailstones originate at an altitude of about 3000{\,{\rm{m}}}, although this varies. As they fall, air resistance slows down the hailstones considerably. In one model of air resistance, the speed of a hailstone of mass m as a function of time t is given by v(t)=\dfrac{mg}{k}( 1-e^{-kt/m}) {\,{\rm{m}}}/\!{\,{\rm{s}}}, where g=9.8{\,{\rm{m}}}/\!{\,{\rm{s}}}^{2} is the acceleration due to gravity and k is a constant that depends on the size of the hailstone and the conditions of the air.
- (a) Find the acceleration a(t) of a hailstone as a function of time t.
- (b) Find \lim\limits_{t\rightarrow \infty} v(t) . What does this limit say about the speed of the hailstone?
- (c) Find \lim\limits_{t\rightarrow \infty} a(t). What does this limit say about the acceleration of the hailstone?
- (a) a(t)=g e^{-\frac{k t}{m}}
- (b) mg/k
- (c) 0
Mean Earnings The mean earnings E, in dollars, of workers 18 years and over are given in the table below:
Year 1975 1980 1985 1990 1995 2000 2005 2010 Mean Earnings 8,552 12,665 17,181 21,793 26,792 32,604 41,231 49,733 - (a)
 Find the exponential function of best fit and show that it equals E=E( t) =9296(1.05)^{t}, where t is the number of years since 1974.
Find the exponential function of best fit and show that it equals E=E( t) =9296(1.05)^{t}, where t is the number of years since 1974. - (b) Find the rate of change of E with respect to t.
- (c) Find the rate of change at t=26 (year 2000).
- (d) Find the rate of change at t=31 (year 2005).
- (e) Find the rate of change at t=36 (year 2010).
- (f) Compare the answers to (c), (d), and (e). Interpret each answer and explain the differences.
- (a)
Rectilinear Motion An object moves in rectilinear motion so that at time t>0 its distance s from the origin is s=s( t) . The velocity v of the object is v=\dfrac{ds}{dt}, and its acceleration is a=\dfrac{dv}{dt}=\dfrac{d^{2}s}{dt^{2}}. If the velocity v=v ( s) is expressed as a function of s, show that the acceleration a can be expressed as a=v\dfrac{dv}{ds}.
See Student Solutions Manual.
Student Approval Professor Miller’s student approval rating is modeled by the function Q( t) =21+\dfrac{10\sin \left(\dfrac{2\pi t}{7}\right) }{\sqrt{t}-\sqrt{20}}, where 0≤ t≤ 16 is the number of weeks since the semester began.
- (a) Find Q^\prime ( t) .
- (b) Evaluate Q^\prime (1) , Q^\prime (5) , and Q^\prime \left( 10\right) .
- (c) Interpret the results obtained in (b).
- (d)
 Use graphing technology to graph Q( t) and Q^\prime ( t) .
Use graphing technology to graph Q( t) and Q^\prime ( t) . - (e) How would you explain the results in (d) to Professor Miller?
Source: Mathematics students at Millikin University, Decatur, Illinois.
208

Angular Velocity If the disk in the figure is rotated about the vertical through an angle \theta , torsion in the wire attempts to turn the disk in the opposite direction. The motion \theta at time t (assuming no friction or air resistance) obeys the equation \theta ( t) =\dfrac{\pi }{3}\cos \left( \dfrac{1}{2}\sqrt{\dfrac{2k}{5}}t\right) where k is the coefficient of torsion of the wire.
- (a) Find the angular velocity \omega =\dfrac{d\theta }{dt} of the disk at any time t.
- (b) What is the angular velocity at t=3?
(a) 
(b) 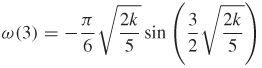

Harmonic Motion A weight hangs on a spring making it 2{\,{\rm{m}}} long when it is stretched out (see the figure). If the weight is pulled down and then released, the weight oscillates up and down, and the length l of the spring after t seconds is given by l( t) =2+\cos \left(2\pi t\right) .
- (a) Find the length l of the spring at the times t=0,\dfrac{1}{2},1,\dfrac{3}{2}, and \dfrac{5}{8}.
- (b) Find the velocity v of the weight at time t=\dfrac{1}{4}.
- (c) Find the acceleration a of the weight at time t=\dfrac{1}{4}.
Find F^\prime (1) if f(x)=\sin x and F(t)=f(t^{2}-1).
F'(1)=2
Normal Line Find the point on the graph of y=e^{-x} where the normal line to the graph passes through the origin.
Use the Chain Rule and the fact that {\cos x=\sin \left(\dfrac{\pi }{2}-x\right) } to show that \dfrac{d}{dx}\cos x=-\sin x.
See Student Solutions Manual.
If y=e^{2x}, show that y^{\prime\prime} -4y=0.
If y=e^{-2x}, show that y^{\prime\prime} -4y=0.
See Student Solutions Manual.
If y=Ae^{2x}+Be^{-2x}, where A and B are constants, show that y^{\prime\prime} -4y=0.
If y=Ae^{ax}+Be^{-ax}, where A, B, and a are constants, show that y^{\prime\prime} -a^{2}y=0.
See Student Solutions Manual.
If y=Ae^{2x}+Be^{3x}, where A and B are constants, show that y^{\prime\prime} -5y^\prime +6y=0.
If y=Ae^{-2x}+Be^{-x}, where A and B are constants, show that y^{\prime\prime} +3y^\prime +2y=0.
See Student Solutions Manual.
If y=A~\sin ( \omega t) +B~\cos (\omega t) , where A, B, and \omega are constants, show that y^{\prime \prime }+\omega ^{2}y=0.
Show that \dfrac{d}{dx}f(h(x))=2xg(x^{2}) , if \dfrac{d}{dx}f(x)=g(x) and h(x)=x^{2}.
See Student Solutions Manual.
Find the nth derivative of f(x)=(2x+3)^{n}.
Find a general formula for the nth derivative of y.
- (a) y=e^{ax}
- (b) y=e^{-ax}
- (a) y^{(n)}(x)=a^ne^{ax}
- (b) y^{(n)}(x)=(-1)^na^n e^{-ax}
- (a) What is \dfrac{d^{10}}{dx^{10}}\sin (ax)?
- (b) What is \dfrac{d^{25}}{dx^{25}}\sin (ax) ?
- (c) Find the nth derivative of f(x)=\sin (ax).
- (a) What is \dfrac{d^{11}}{dx^{11}}\cos (ax)?
- (b) What is \dfrac{d^{12}}{dx^{12}}\cos (ax) ?
- (c) Find the nth derivative of f(x)=\cos (ax).
- (a) {d^{11}\cos(ax)\over dx^{11}}=a^{11} \sin (a x)
- (b) {d^{12}\cos(ax)\over dx^{12}}=a^{12} \cos (a x)
- (c) f^{(n)}(x)=-a^n\sin (ax), n=1+4k, k=0,1,2,3,\ldots; f^{(n)}(x)=-a^n \cos(ax), n=2+4k, k=0,1,2,3,\ldots; f^{(n)}(x)=a^n\sin (ax), n=3+4k, k=0,1,2,3,\ldots; f^{(n)}(x)=a^n \cos(ax), n=4+4k, k=0,1,2,3,\ldots
If y=e^{-at}~[ A~\sin ( \omega t) +B~\cos ( \omega t) ] , where A, B, a, and \omega are constants, find y^\prime and y^{\prime\prime} .
Show that if a function f has the properties:
- f(u+v)=f(u)f(v) for all choices of u and v
- f(x)=1+xg(x), where \lim\limits_{x\rightarrow 0}g(x)=1,
then f^\prime =f.
See Student Solutions Manual.
Challenge Problems
Find the nth derivative of f(x)=\dfrac{1}{3x-4}.
Let f_{1}(x),\ldots ,f_{n}(x) be n differentiable functions. Find the derivative of y=f_{1}(f_{2}(f_{3} (\ldots (f_{n}(x)\ldots )))).
See Student Solutions Manual.
Let f(x)=\left\{ \begin{array}{c@{\qquad}ll} x^{2}\sin {\dfrac{1}{x}} & \hbox{if} & x\;≠ 0 \\ 0 & \hbox{if} & x\;=0 \end{array} \right.
Show that f^\prime (0) exists, but that f^\prime (x) is not continuous at 0.
Define f by f(x)=\left\{ \begin{array}{l@{\quad}ll} e^{-1/x^{2}} & \hbox{if}& x\;≠ 0 \\ 0 & \hbox{if}& x\;=0 \end{array} \right.
Show that f is differentiable on (-\infty ,\infty ) and find f^\prime (x) for each value of x. [Hint: To find f^\prime (0), use the definition of the derivative. Then show that 1< x^{2}e^{1/x^{2}} for x≠ 0.]
See Student Solutions Manual.
Suppose f( x) =x^{2} and g( x) =\left\vert x-1\right\vert . The functions f and g are continuous on their domains, the set of all real numbers.
- (a) Is f differentiable at all real numbers? If not, where does f^\prime not exist?
- (b) Is g differentiable at all real numbers? If not, where does g^\prime not exist?
- (c) Can the Chain Rule be used to differentiate the composite function ( f\circ g) (x) for all x? Explain.
- (d) Is the composite function ( f\circ g) (x) differentiable? If so, what is its derivative?
Suppose f( x) =x^{4} and g( x) =x^{1/3}. The functions f and g are continuous on their domains, the set of all real numbers.
- (a) Is f differentiable at all real numbers? If not, where does f^\prime not exist?
- (b) Is g differentiable at all real numbers? If not, where does g^\prime not exist?
- (c) Can the Chain Rule be used to differentiate the composite function ( f\circ g) (x) for all x? Explain.
- (d) Is the composite function ( f\circ g) (x) differentiable? If so, what is its derivative?
See Student Solutions Manual.
The function f(x)=e^{x} has the property f^\prime (x)=f(x). Give an example of another function g(x) such that g(x) is defined for all real x, g^{\prime }(x)=g(x), and g(x)≠ f(x).
Harmonic Motion The motion of the piston of an automobile engine is approximately simple harmonic. If the stroke of a piston (twice the amplitude) is 10{\,{\rm{cm}}} and the angular velocity \omega is 60 revolutions per second, then the motion of the piston is given by s( t) =5\sin ( 120\pi t ) {\,{\rm{cm}}}.
- (a) Find the acceleration a of the piston at the end of its stroke \left(t=\frac{1}{240} {\rm second}\right).
- (b) If the piston weighs 1{\,{\rm{kg}}}, what resultant force must be exerted on it at this point? (Hint: Use Newton’s Second Law, that is, F=ma.)
- (a) -72,000\pi^2\; \mathsf{\small cm/sec^2}
- (b) 72,000 \pi^2\; \mathsf{\small kg \cdot cm/sec^2}
