3.2 Assess Your UnderstandingPrinted Page 218
Concepts and Vocabulary
True or False If f is a one-to-one differentiable function and if f′(x)>0, then f has an inverse function whose derivative is positive.
True
True or False ddxtan−1x=11+x2, where −∞<x<∞.
True
True or False Implicit differentiation is a technique for finding the derivative of an implicitly defined function.
True
ddxsin−1x= ______, −1<x<1.
1√1−x2
True or False If yq=xp for integers p and q, then qyq−1=pxp−1.
False
ddx(3x1/3)= ______.
1x2/3
Skill Building
In Problems 7–30, find y′=dydx using implicit differentiation.
x2+y2=4
y′=−xy
y4−4x2=4
ey=sinx
y′=cosxey
ey=tanx
ex+y=y
y′=−ex+yex+y−1
ex+y=x2
x2y=5
y′=−2yx
x3y=8
x2−y2−xy=2
y′=2x−y2y+x
x2−4xy+y2=y
1x+1y=1
y′=−y2x2
1x−1y=4
x2+y2=2yx
y′=x3+yx(1−xy)
x2+y2=2y2x2
exsiny+eycosx=4
y′=eysinx−exsinyexcosy+eycosx
eycosx+e−xsiny=10
219
(x2+y)3=y
y′=−6x(x2+y)23(x2+y)2−1
(x+y2)3=3x
y=tan(x−y)
y′=sec2(x−y)1+sec2(x−y)
y=cos(x+y)
y=xsiny
y′=siny1−xcosy
y=xcosy
x2y=exy
y′=yexy−2xyx2−xexy
yex=y−x
In Problems 31–56, find y′.
y=x2/3+4
y′=23x1/3
y=x1/3−1
y=3√x2
y′=23x1/3
y=4√x5
y=3√x−13√x
y′=13x2/3+13x4/3
y=√x+1√x
y=(x3−1)1/2
y′=3x22(x3−1)1/2
y=(x2−1)1/3
y=x√x2−1
y′=(x2−1)1/2+x2(x2−1)1/2
y=x√x3+1
y=e√x2−9
y′=xe(x2−9)1/2(x2−9)1/2
y=√ex
y=(x2cosx)3/2
y′=32(x2cosx)1/2(2xcosx−x2sinx)
y=(x2sinx)3/2
y=(x2−3)3/2(6x+1)5/3
y′=3x(x2−3)1/2(6x+1)5/3+10(x2−3)3/2(6x+1)2/3=(6x+1)2/3(x2−3)1/2(28x2+3x−30)
y=(2x3−1)4/3(3x+4)5/2
y=sin−1(4x)
y′=4√1−16x2
y=cos−1x2
y=sec−1(3x)
y′=1x√9x2−1
y=tan−1(1x)
y=sin−1ex
y′=ex√1−e2x
y=sin−1(1−x2)
y=x(sin−1x)
y′=sin−1x+x√1−x2
y=xtan−1(x+1)
y=tan−1(sinx)
y′=cosx1+sin2x
y=sin(tan−1x)
In Problems 57–62, find y′ and y′′.
x2+y2=4
y′=−xy, y″
x^{2}-y^{2}=1
xy^2+yx^{2}=2
y'=-{y^2+2xy\over x^2+2xy}, y''= \dfrac{6xy(x + y)(x^2 + xy + y^2)}{(x^2 + 2xy)^3}
4xy=x^{2}+y^{2}
y=\sqrt{x^{2}+1}
y'={x\over (x^2+1)^{1/2}}, y''= \dfrac{1}{(x^2+1)^{3/2}}
y=\sqrt{4-x^{2}}
In Problems 63–68 for each implicitly defined equation:
- (a) Find the slope of the tangent line to the graph of the equation at the indicated point.
- (b) Write an equation for this tangent line.
- (c) Graph the tangent line on the same axes as the graph of the equation.
x^{2}+y^{2}=5 at (1,\,2)
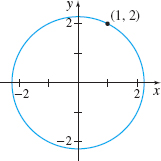
- (a) -1/2
- (b) y=-\dfrac{x}{2}+\dfrac{5}{2}
- (c)

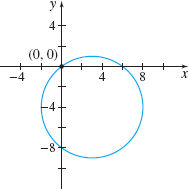
(x-3) ^{2} + (y+4) ^{2}=25 at (0,0)
x^{2}-y^{2}=8 at (3,1)

- (a) 3
- (b) y=3x-8
- (c)

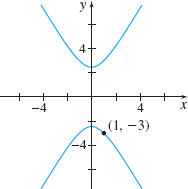
y^{2}-3x^{2}=6 at (1,-3)
\dfrac{x^{2}}{4}+\dfrac{y^{2}}{3}=1 at \left(-1,\dfrac{3}{2}\right)
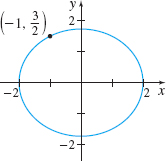
- (a) 1/2
- (b) y=\dfrac{x}{2}+2
- (c)
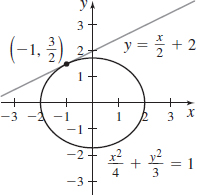
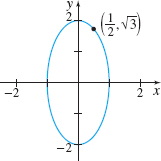
x^{2}+\dfrac{y^{2}}{4}=1 at \left( \dfrac{1}{2},\sqrt{3}\right)
Find y^\prime and y^{\prime\prime} at the point (-1,1) on the graph of 3x^{2}y+2y^{3}=5x^{2}
y'=-4/9; y''=-100/243
Find y^\prime and y^{\prime\prime} at the point (0,0) on the graph of 4x^{3}+2y^{3}=x+y.
In Problems 71–76, the functions f and g are inverse functions.
If f\,(0)=4 and f^\prime (0)=-2, find g^\prime(4).
g'(4)=-1/2
If f(1)=-2 and f^\prime (1)=4, find g^\prime (-2).
If g(3)=-2\,and g^\prime (3)=\dfrac{1}{2}, find f^\prime(-2).
f'(-2)=2
If g(-1)=0 and g^\prime (-1)=-\dfrac{1}{3}, find f^\prime (0).
The function f(x)=x^{3}+2x has an inverse function g. Find g^\prime (0) and g^\prime (3).
g'(0)=1/2, g'(3)=1/5
The function f(x)=2x^{3}+x-3 has an inverse function g. Find g^\prime (-3) and g^\prime (0).
Applications and Extensions
In Problems 77–84, find y^\prime .
(Hint: Use the fact that \vert x\vert=\sqrt{x^{2}}.)
y=|3x|
y'=3x/|x|
y=|x^{5}|
y=|2x-1|
y'={2(2x-1)\over |2x-1|}
y=|5-x^{2}|
y=|\cos x|
y'=-\dfrac{\sin x \,\cos x}{|\cos x|}
y=|\sin x|
y=\sin |x|
y'=\cos|x|\cdot \dfrac{x}{|x|}
\vert x\vert +\vert \,y\vert =1
220
Tangent Line to a Hypocycloid The graph of x^{2/3}+y^{2/3}=5 is called a hypocycloid. Part of its graph is shown in the figure. Find an equation of the tangent line to the hypocycloid at the point ( 1,8).
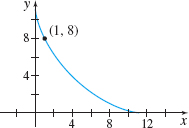
y=-2x+10
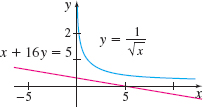
Tangent Line At what point does the graph of y=\dfrac{1}{\sqrt{x}} have a tangent line parallel to the line x+16y=5? See the figure.
Tangent Line to a Cardioid The graph of (x^{2}+y^{2}+2x) ^{2}= 4 ( x^{2}+y^{2}), called a cardioid, is shown in the figure.
- (a) Find all the points on the cardioid that have a horizontal tangent line. Ignore the origin.
- (b) Find all the points on the cardioid that have a vertical tangent line. Ignore the origin.
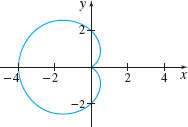
- (a) (-3/2,\pm 3\sqrt{3}/2)
- (b) (-4,0), (1/2,\pm \sqrt{3}/2)
Tangent Line to a Cardioid The graph of \begin{eqnarray*} (x^{2}+y^{2}+y) ^{2}= ( x^{2}+y^{2}) \end{eqnarray*} is a cardioid.
- (a) Find all the points on the cardioid that have a horizontal tangent line. Ignore the origin.
- (b) Find all the points on the cardioid that have a vertical tangent line. Ignore the origin.
- (c)
 Graph the cardioid and any horizontal or vertical tangent lines.
Graph the cardioid and any horizontal or vertical tangent lines.
Tangent Line For the equation x+xy+2y^{2}=6:
- (a) Find an expression for the slope of the tangent line at any point (x, y) on the graph.
- (b) Write an equation for the line tangent to the graph at the point (2,1).
- (c) Find the coordinates of any other point on this graph with slope equal to the slope at (2,1).
- (d)
 Graph the equation and the tangent lines found in parts (b) and (c) on the same screen.
Graph the equation and the tangent lines found in parts (b) and (c) on the same screen.
- (a) y'=\frac{-y-1}{x+4 y}
- (b) y=-{1\over 3}x+{5\over 3}
- (c) (6,-3)
- (d)
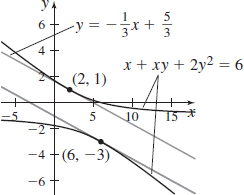
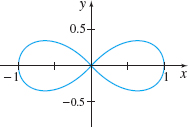
Tangent Line to a Lemniscate The graph of (x^{2}+y^{2})^{2}= x^{2}-y^{2}, called a lemniscate, is shown in the figure. There are exactly four points at which the tangent line to the lemniscate is horizontal. Find them.
Tangent Line
- (a) Find an equation for the tangent line to the graph of y=\sin ^{-1}\dfrac{x}{2} at the point (0,0).
- (b)
 Graph y=\sin ^{-1}\dfrac{x}{2} and the tangent line at (0,0) .
Graph y=\sin ^{-1}\dfrac{x}{2} and the tangent line at (0,0) .
- (a) y={1\over 2}x
- (b)
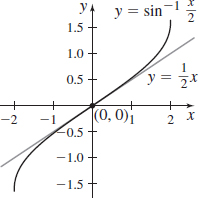
Physics For ideal gases, Boyle’s law states that pressure is inversely proportional to volume. A more realistic relationship between pressure P and volume V is given by the van der Waals equation P+{\frac{a}{V^{2}}}={\frac{C}{V-b}} where C is the constant of proportionality, a is a constant that depends on molecular attraction, and b is a constant that depends on the size of the molecules. Find \dfrac{dV}{dP}, which measures the compressibility of the gas.
Rectilinear Motion An object of mass m moves in rectilinear motion so that at time t>0 its distance s from the origin and its velocity v=\dfrac{ds}{dt} satisfy the equation m\big(v^{2}-v_{0}^{2}\big)=k\big(s_{0}^{2}-s^{2}\big) where k is a positive constant and v_{0} and s_{0} are the initial velocity and position, respectively, of the object. Show that if v>0, then ma=-ks where a=\dfrac{d^{2}s}{dt^{2}} is the acceleration of the object.
[Hint: Differentiate the expression m\big(v^{2}-v_{0}^{2}\big)=k\big(s_{0}^{2}-s^{2}\big) with respect to t.]
See Student Solutions Manual.
Price Function It is estimated that t months from now the average price (in dollars) of a tablet will be given by P( t) =\dfrac{300}{1+\dfrac{1}{6}\sqrt{t}}+100, \ 0≤ t≤ 60.
- (a) Find P^\prime ( t)
- (b) Find P^\prime ( 0), P^\prime ( 16), and P^\prime ( 49) and interpret the results.
- (c)
 Graph P =P ( t), and explain how the graph supports the answers in (b).
Graph P =P ( t), and explain how the graph supports the answers in (b).
Production Function The production of commodities sometimes requires several resources such as land, labor, and machinery. If there are two inputs that require amounts x and y, then the output z is given by the function of two variables: z=f( x,y) . Here, z is called a production function. For example, if x represents land, y represents capital, and z is the amount of a commodity produced, a possible production function is z=x^{0.5}y^{0.4}. Set z equal to a fixed amount produced and show that \dfrac{dy}{dx}=-\dfrac{5y}{4x}. This illustrates that the rate of change of capital with respect to land is always negative when the amount produced is fixed.
See Student Solutions Manual.
Learning Curve The psychologist L. L. Thurstone suggested the following function for the time T it takes to memorize a list of n words: T=f( n) =Cn\sqrt{n-b}, where C and b are constants depending on the person and the task.
- (a) Find the rate of change in time T with respect to the number n of words to be memorized.
221
- (b) Suppose that for a certain person and a certain task, C=2 and b=2. Find f^\prime (10) and f^\prime (30) .
- (c) Interpret the results found in (c).
- (a) Find the rate of change in time T with respect to the number n of words to be memorized.
The Folium of Descartes The graph of the equation x^{3}+y^{3}=2xy is called the Folium of Descartes.
- (a) Find y^\prime .
- (b) Find an equation of the tangent line to the Folium of Descartes at the point (1,1).
- (c) Find any points on the graph where the tangent line to the graph is horizontal. Ignore the origin.
- (d)
 Graph the equation x^{3}+y^{3}=2xy. Explain how the graph supports the answers to (b) and (c).
Graph the equation x^{3}+y^{3}=2xy. Explain how the graph supports the answers to (b) and (c).
- (a) y'=\frac{3 x^2-2 y}{2 x-3 y^2}
- (b) y=-x+2
- (c) \left(\dfrac{2^{4/3}}{3},\dfrac{2^{5/3}}{3}\right)
- (d)
If n is an even positive integer, show that the tangent line to the graph of y=\sqrt[n]{x} at (1,1) is perpendicular to the tangent line to the graph of y=x^{n} at (-1,1).
At what point(s), if any, is the line y=x-1 parallel to the tangent line to the graph of y=\sqrt{25-x^{2}}?
\left(-\dfrac{5\sqrt{2}}{2},\dfrac{5\sqrt{2}}{2}\right)
What is wrong with the following?
If x+y=e^{x+y}, then 1+y^\prime =e^{x+y}(1+y^\prime). Since e^{x + y} > 0, then y^\prime = -1 for all x. Therefore, x+y=e^{x+y} must be a line of slope -1.
Show that if a function y is differentiable, and x and y are related by the equation x^{n}y^{m}+x^{m}y^{n}=k, where k is a constant, then {\dfrac{dy}{dx}}=-{\dfrac{y(nx^{r}+my^{r})}{x(mx^{r}+ny^{r})}} \qquad \hbox{where}\quad r=n-m
See Student Solutions Manual.
If g(x)=\cos ^{-1}(\cos x), show that g^\prime (x)=\dfrac{\sin x}{|\sin x|}.
Show that \dfrac{d}{dx}\tan ^{-1}(\cot x)=-1.
See Student Solutions Manual.
Show that \dfrac{d}{dx}\cot ^{-1}x=\dfrac{d}{dx}\tan ^{-1} \dfrac{1}{x} for all x≠ 0.
Establish the identity \sin ^{-1}x+\cos ^{-1}x=\dfrac{\pi }{2} by showing that the derivative of y=\sin ^{-1}x+\cos ^{-1}x is 0. Use the fact that when x=0, then y=\dfrac{\pi }{2}.
See Student Solutions Manual.
Establish the identity \tan ^{-1}x+\cot ^{-1}x=\dfrac{\pi }{2} by showing that the derivative of y=\tan ^{-1}x+\cot ^{-1}x is 0. Use the fact that when x=1, then y=\dfrac{\pi }{2}.
Tangent Line Show that an equation for the tangent line at any point ( x_{0},y_{0}) on the ellipse \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1 is \dfrac{xx_{0}}{a^{2}}+\dfrac{yy_{0}}{b^{2}}=1.
See Student Solutions Manual.
Tangent Line Show that the slope of the tangent line to a hypocycloid x^{2/3}+y^{2/3}=a^{2/3}, a>0, at any point for which x≠ 0, is -\dfrac{y^{1/3}}{x^{1/3}}.
Tangent Line Use implicit differentiation to show that the tangent line to a circle x^{2}+y^{2}=R^{2} at any point P on the circle is perpendicular to OP, where O is the center of the circle.
See Student Solutions Manual.
Challenge Problems
Let A=\left( 2,1\right) and B=\left( 5,2\right) be points on the graph of f(x)=\sqrt{x-1}. A line is moved upward on the graph so that it remains parallel to the secant line AB. Find the coordinates of the last point on the graph of f before the secant line loses contact with the graph.
Orthogonal Graphs Problems 111 and 112 require the following definition:
The graphs of two functions are said to be orthogonal if the tangent lines to the graphs are perpendicular at each point of intersection.
- (a) Show that the graphs of xy=c_{1} and -x^{2}+y^{2}=c_{2} are orthogonal, where c_{1} and c_{2} are positive constants.
- (b)
 Graph each function on one coordinate system for c_{1}=1,\,2,\,3 and c_{2}=1,\,9,\,25.
Graph each function on one coordinate system for c_{1}=1,\,2,\,3 and c_{2}=1,\,9,\,25.
- (a) {dy\over dx}=-\dfrac{y}{x} for the first and {dy\over dx}=\dfrac{x}{y} for the second.
- (b)

Find a>0 so that the parabolas y^{2}=2ax+a^{2} and y^{2}=a^{2}-2ax are orthogonal.
Show that if p and q>0 are integers, then y=x^{p/q} is a differentiable function of x.
See Student Solutions Manual.
We say that y is an algebraic function of x if it is a function that satisfies an equation of the form P_{0}(x)y^{n}+P_{1}(x)y^{n-1}+\cdots +P_{n-1}(x)y+P_{n}(x)=0 where P_{k}(x), k=0,1,2,\ldots, n, are polynomials. For example, y=\sqrt{x} satisfies y^{2}-x=0 Use implicit differentiation to obtain a formula for the derivative of an algebraic function.
Another way of finding the derivative of y=\sqrt[n]{x} is to use inverse functions. The function y=f(x)=x^{n},n a positive integer, has the derivative f^\prime ( x) = nx^{n-1}. So, if x≠ 0, then f^{\prime }(x)≠ 0. The inverse function of f, namely, x=g(y)=\sqrt[n]{y}, is defined for all y, if n is odd, and for all y ≥ 0, if n is even. Since this inverse function is differentiable for all y≠ 0, we have g^\prime (y)=\frac{d}{dy}\sqrt[n]{y}=\frac{1}{f^\prime (x)}=\frac{1}{nx^{n-1}} Since nx^{n-1}=n\left( \sqrt[n]{y}\right) ^{n-1}=ny^{(n-1)/n}=ny^{1-(1/n)}, we have \frac{d}{dy}\sqrt[n]{y}=\frac{d}{dy}y^{1/n}=\frac{1}{ny^{1-(1/n)}}=\frac{1}{n}y^{(1/n)-1} Use the result from above and the Chain Rule to prove the formula \frac{d}{dx}x^{p/q}=\frac{p}{q}x^{(p/q)-1}
See Student Solutions Manual.
- (a) You might try to infer from Problem 104 that \cot ^{-1}x= \tan ^{-1}\dfrac{1}{x}+C for all x≠ 0, where C is a constant. Show, however, that \cot ^{-1}x=\left\{ \begin{array}{l@{\qquad}l} \tan ^{-1}\dfrac{1}{x} & \hbox{if}\; x>0 \\ \tan ^{-1}\dfrac{1}{x}+\pi & \hbox{if}\; x<0 \end{array} \right.
- (b) What is an explanation of the incorrect inference?
