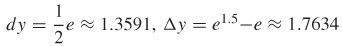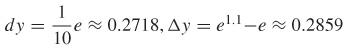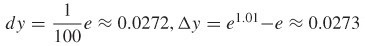More About Derivatives

3.4 Assess Your Understanding
Printed Page 237

Concepts and Vocabulary

Multiple Choice If $y=f( x)$ is a differentiable function, the differential $dy=$ [(a) $\Delta y,$ (b) $\Delta x,$ (c) $f(x) dx,$ (d) $f^\prime(x) dx$ ].

(d)

A linear approximation to a differentiable function $f$ near $x_{0}$ is given by the function $L(x)=$ ______.

$f(x_0)+f'(x_0)(x-x_0)$

True or False The difference $\vert \Delta y-dy\vert$ measures the departure of the graph of $y=f( x)$ from the graph of the tangent line to $f$ .

True

If $Q$ is a quantity to be measured and $\Delta Q$ is the error made in measuring $Q$ , then the relative error in the measurement is given by the ratio ______.

$\dfrac{|\Delta Q|}{Q(x_0)}$

True or False Newton’s Method uses tangent lines to the graph of $f$ to approximate the zeros of $f$ .

True

True or False Before using Newton’s Method, we need a first approximation for the zero.

True

Skill Building

In Problems 7–16, find the differential $dy$ of each function.

$y=x^{3}-2x+1$

$dy=(3x^2-2)\,dx$

$y=e^{x}+2x-1$

$y=4(x^{2}+1)^{3/2}$

$dy=12x(x^2+1)^{1/2}\,dx$

$y=\sqrt{x^{2}-1}$

$y=3\sin (2x) +x$

$dy=(6\cos(2x)+1)\,dx$

$y=\cos ^{2}(3x) -x$

$y=e^{-x}$

$dy=-e^{-x}\,dx$

$y=e^{\sin x}$

$y=xe^{x}$

$dy=(e^x+xe^x)\,dx$

$y=\dfrac{e^{-x}}{x}$

In Problems 17–22:

Find the differential $dy$ for each function $f$ .
(b) Evaluate $dy$ and $\Delta y$ at the given value of $x$ when (i) $\Delta x=0.5$ , (ii) $\Delta x=0.1$ , and (iii) $\Delta x=0.01$ .
(c) Find the error $\vert \Delta y-dy\vert$ for each choice of $dx = \Delta x$ .

$f(x) =e^{x}$ at $x=1$

$dy=e^xdx$
(b)
(c)
1. 0.4043
2. 0.0141
3. 0.000136

$f(x) =e^{-x}$ at $x=1$

$f(x) =x^{2/3}$ at $x=2$

(a)
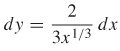
(b)
1. $dy ≈ 0.2646$ , $\Delta y ≈ 0.2546$
2. $dy ≈ 0.0529$ , $\Delta y ≈ 0.0525$
3. $dy ≈ 0.0053$ , $\Delta y ≈ 0.0053$ ;
(c)
1. 0.009952,
2. 0.000431,
3. $4\times10^{-6}$

$f(x) =x^{-1/2}$ at $x=1$

$f(x) =\cos x$ at $x=\pi$

$dy=-\sin x\,dx$
(b)
1. $dy=0$ , $\Delta y ≈ 0.1224$
2. $dy=0$ , $\Delta y ≈ 0.005$
3. $dy=0$ , $\Delta y ≈ 0.00005$ ;
(c)
1. 0.1224,
2. 0.005
3. 0.00005

$f(x) =\tan x$ at $x=0$

In Problems 23–30:

(a) Find the linear approximation $L(x)$ to $f$ at $x_{0}$ .
(b) Graph $f$ and $L$ on the same set of axes.

$f(x)=(x+1) ^{5},\quad x_{0}=2$

$L(x)=405 x-567$
(b)

$f(x)=x^{3}-1,\quad x_{0}=0$

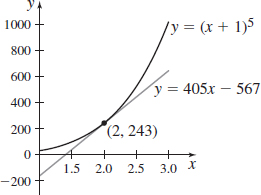
$f(x)=\sqrt{x},\quad x_{0}=4$

$L(x)=\dfrac{x}{4}+1$
(b)

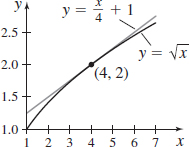
$f(x)=x^{2/3},\quad x_{0}=1$

$f(x)=\ln x,\quad x_{0}=1$

$L(x)=x-1$
(b)

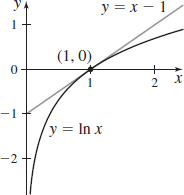
$f(x) =e^{x},$ $x_{0}=1$

$f(x)=\cos x,\quad x_{0}=\dfrac{\pi }{3}$

$L(x)=-\dfrac{\sqrt{3} x}{2}+\dfrac{\pi }{2 \sqrt{3}}+\frac{1}{2}$
(b)

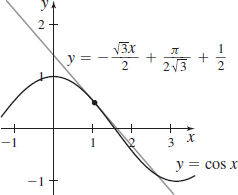
$f(x)=\sin x,\quad x_{0}=\dfrac{\pi }{6}$

Approximate the change in:
1. $y=f(x)=x^{2}$ as $x$ changes from $3$ to $3.001$ .
2. $y=f(x)=\dfrac{1}{x+2}$ as $x$ changes from $2$ to $1.98.$

(a) 0.006
$0.00125$

Approximate the change in:
1. $y=x^{3}$ as $x$ changes from $3$ to $3.01$ .
2. $y=\dfrac{1}{x-1}$ as $x$ changes from $2$ to $1.98.$

In Problems 33–40, for each function:

(a) Use the Intermediate Value Theorem to confirm that a zero exists in the given interval.
(b) Use Newton’s Method with the first approximation $c_{1}$ to find $c_{3}$ , the third approximation to the real zero.

$f(x) = x^{3}+3x-5$ , interval: $(1, 2).$ Let $c_{1}=1.5.$

(a) See Student Solutions Manual.
$c_3=1.155$

$f(x) = x^{3}-4x+2$ , interval: $(1,2).$ Let $c_{1}=1.5$ .

$f(x) = 2x^{3}+3x^{2}+4x-1$ , interval: $(0,1).$ Let $c_{1}=0.5.$

(a) See Student Solutions Manual.
$c_3=0.214$

$f(x) = x^{3}-x^{2}-2x+1$ , interval: $(0,1) .$ Let $c_{1}=0.5$

$f(x) = x^{3}-6x-12$ , interval: $( 3,4) .$ Let $c_{1}=3.5.$

(a) See Student Solutions Manual.
$c_3=3.136$

238

$f(x) = 3x^{3}+5x-40$ , interval: $( 2,3) .$ Let $c_{1}=2.5.$

$f(x) = x^{4}-2x^{3}+21x-23$ , interval: $(1,2).$ Use a first approximation $c_{1}$ of your choice.

(a) See Student Solutions Manual.
(b) Answers will vary.

$f(x) = x^{4}-x^{3}+x-2$ , interval: $(1,2).$ Use a first approximation $c_{1}$ of your choice.

In Problems 41–46, for each function:

(a) Use the Intermediate Value Theorem to confirm that a zero exists in the given interval.
Use graphing technology with Newton’s Method to find $c_{5}$ , the fifth approximation to the real zero. Use the midpoint of the interval for the first approximation $c_{1}$ .

$f(x) =x+e^{x},$ interval: $(-1,0)$

(a) See Student Solutions Manual.
$c_5 ≈ -0.567$

$f(x)=x-e^{-x},$ interval: $(0,1)$

$f( x) =x^{3}+\cos ^{2}x,$ interval: $(-1,0)$

(a) See Student Solutions Manual.
$c_5 ≈ -0.791$

$f( x) =x^{2}+2\sin x-0.5,$ interval: $(0,1)$

$f(x) =5-\sqrt{x^{2}+2},$ interval: $(4,5)$

(a) See Student Solutions Manual.
$c_5 ≈ 4.796$

$f( x) =2x^{2}+x^{2/3}-4,$ interval: $(1,2)$

Applications and Extensions

Area of a Disk A circular plate is heated and expands. If the radius of the plate increases from $R=10$ cm to $R=10.1$ cm, use differentials to approximate the increase in the area of the top surface.

$2\pi$

Volume of a Cylinder In a wooden block $3$ cm thick, an existing circular hole with a radius of $2$ cm is enlarged to a hole with a radius of $2.2$ cm. Use differentials to approximate the volume of wood that is removed.

Volume of a Balloon Use differentials to approximate the change in volume of a spherical balloon of radius $3$ m as the balloon swells to a radius of $3.1$ m.

$3.6\pi\;\mathsf{m^3}$

Volume of a Paper Cup A manufacturer produces paper cups in the shape of a right circular cone with a radius equal to one-fourth its height. Specifications call for the cups to have a top diameter of 4 cm. After production, it is discovered that the diameter measures only 3.8 cm. Use differentials to approximate the loss in capacity of the cup.

Volume of a Sphere
1. (a) Use differentials to approximate the volume of material needed to manufacture a hollow sphere if its inner radius is 2 m and its outer radius is 2.1 m.
2. (b) Is the approximation overestimating or underestimating the volume of material needed?
3. Discuss the importance of knowing the answer to (b) if the manufacturer receives an order for $10,000$ spheres.

$1.6\pi\;\mathsf{m^3}$
(b) Underestimate
(c) Answers will vary.

Distance Traveled A bee flies around a circle traced on an equator of a ball with a radius of 7 cm at a constant distance of 2 cm from the ball. An ant travels along the same circle but on the ball.
1. (a) Use differentials to approximate how many more centimeters the bee travels than the ant in one round trip.
2. (b) Does the linear approximation overestimate or underestimate the difference in the distances the bugs travel? Explain.

Estimating Height To find the height of a building, the length of the shadow of a 3-m pole placed 9 m from the building is measured. See the figure. This measurement is found to be 1 m, with a percentage error of 1%. Use differentials to approximate the height of the building. What is the percentage error in the estimate?

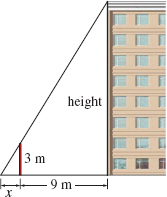
30 ± 0.27m; 0.9%

Pendulum Length The period of the pendulum of a grandfather clock is $T=2\pi \sqrt{\dfrac{l}{g}}$ , where $l$ is the length (in meters) of the pendulum, $T$ is the period (in seconds), and $g$ is the acceleration due to gravity ( $9.8{\,{\rm{m}}}/\!{\,{\rm{s}}}^{2}$ ). Suppose an increase in temperature increases the length $l$ of the pendulum, a thin wire, by 1%. What is the corresponding percentage error in the period? How much time will the clock lose (or gain) each day?

Pendulum Length Refer to Problem 54. If the pendulum of a grandfather clock is normally 1 m long and the length is increased by $10$ cm, use differentials to approximate the number of minutes the clock will lose (or gain) each day.

72 min

Luminosity of the Sun The luminosity $L$ of a star is the rate at which it radiates energy. This rate depends on the temperature $\ T$ (in Kelvin, where $0{\,{\rm{K}}}$ is absolute zero) and the surface area $A$ of the star’s photosphere (the gaseous surface that emits the light). Luminosity at time $t$ is given by the formula $L(t)=\sigma AT^{4}$ , where $\sigma$ is a constant, known as the Stefan–Boltzmann constant.

As with most stars, the Sun’s temperature has gradually increased over the 5 billion years of its existence, causing its luminosity to slowly increase. For this problem, we assume that increased luminosity $L$ is due only to an increase in temperature $T$ . That is, we treat $A$ as a constant.
1. Find the rate of change of the temperature $T$ of the Sun with respect to time $t$ . Write the answer in terms of the rate of change of the Sun’s luminosity $L$ with respect to time $t$ .
2. $4.5$ billion years ago, the Sun’s luminosity was only 70% of what it is now. If the rate of change of luminosity $L$ with respect to time $t$ is constant, then $\dfrac{\Delta L}{\Delta t}=\dfrac{0.3L_{c}}{\Delta t}=\dfrac{0.3L_{c}}{4.5},$ where $L_{c}$ is the current luminosity. Use differentials to approximate the current rate of change of the temperature $T$ of the Sun in degrees per century.

Climbing a Mountain Weight $W$ is the force on an object due to the pull of gravity. On Earth, this force is given by Newton’s Law of Universal Gravitation: $W=\dfrac{GmM}{r^{2}}$ , where $m$ is the mass of the object, $M=5.974\times 10^{24}{\,{\rm{kg}}}$ is the mass of Earth, $r$ is the distance of the object from the center of the Earth, and $G=6.67\times 10^{-11}{\,{\rm{m}}}^{3}/( {\,{\rm{kg}}}\cdot {\,{\rm{s}}}^{2})$ is the universal gravitational constant. Suppose a person weighs $70{\,{\rm{kg}}}$ at sea level, that is, when $r=6370{\,{\rm{km}}}$ (the radius of Earth). Use differentials to

239

approximate the person’s weight at the top of Mount Everest, which is $8.8$ ${\,{\rm{km}}}$ above sea level.

$9.998$ kg

Body Mass Index The body mass index (BMI) is given by the formula ${\rm BMI} = 703\dfrac{m}{h^{2}}$ where $m$ is the person’s weight in pounds and $h$ is the person’s height in inches. A BMI of $25$ or less indicates that weight is normal, whereas a BMI greater than $25$ indicates that a person is overweight.
1. Suppose a man who is $5{\,{\rm{ft}}}$ $6{\,{\rm{in}}}$ . weighs $142{\,{\rm{lb}}}$ in the morning when he first wakes up, but he weighs $148{\,{\rm{lb}}}$ in the afternoon. Calculate his BMI in the morning and use differentials to approximate the change in his BMI in the afternoon. Round both answers to three decimal places.
2. (b) Did this linear approximation overestimate or underestimate the man’s afternoon weight? Explain.
3. A woman who weighs $165{\,{\rm{lb}}}$ estimates her height at $68{\,{\rm{in}}}$ . with a possible error of $\pm 1.5{\,{\rm{in}}}.$ Calculate her BMI, assuming a height of $68{\,{\rm{in}}}.$ Then use differentials to approximate the possible error in her calculation of BMI. Round the answers to three decimal places.
4. (d) In the situations described in (a) and (c), how do you explain the classification of each person as normal or overweight?

Percentage Error The radius of a spherical ball is found by measuring the volume of the sphere (by finding how much water it displaces). It is determined that the volume is 40 cubic centimeters (cm $^3$ ), with a tolerance of 1%. Find the percentage error in the radius of the sphere caused by the error in measuring the volume.

0.333%

Percentage Error The oil pan of a car has the shape of a hemisphere with a radius of $8{\,{\rm{cm}}}$ . The depth $h$ of the oil is measured at $3{\,{\rm{cm}}}$ , with a percentage error of 10%. Approximate the percentage error in the volume. [Hint: The volume $V$ for a spherical segment is $V=\dfrac{1}{3}\pi h^{2}(3R-h)$ , where $R$ is the radius of the sphere.]

Percentage Error If the percentage error in measuring the edge of a cube is 2%, what is the percentage error in computing its volume?

Focal Length To photograph an object, a camera’s lens forms an image of the object on the camera’s photo sensors. A camera lens can be approximated by a thin lens, which obeys the thin-lens equation $\dfrac{1}{f}=\dfrac{1}{p}+\dfrac{1}{q}$ , where $p$ is the distance from the lens to the object being photographed, $q$ is the distance from the lens to the image of the object, and $f$ is the focal length of the lens. A camera whose lens has a focal length of $50{\,{\rm{mm}}}$ is being used to photograph a dog. The dog is originally $15{\,{\rm{m}}}$ from the lens, but moves $0.33{\,{\rm{m}}}$ (about a foot) closer to the lens. Use differentials to approximate the distance the image of the dog moved.

Using Newton’s Method to Solve Equations In Problems 63–66, use Newton’s Method to solve each equation correct to three decimal places.

$e^{-x}=\ln x$

1.309

$e^{-x}=x-4$

$e^{x}=x^{2}$

-0.703

$e^{x}=2\cos x$ , $x > 0$

Approximating $e$ Use Newton’s Method to approximate the value of $e$ by finding the zero of the equation $\ln x-1=0.$ Use $c_{1}=3$ as the first approximation and find the fourth approximation to the zero. Compare the results from this approximation to the value of $e$ obtained with a calculator.

2.718

Show that the linear approximation of a function $f( x) =( 1+x) ^{k}$ , where $x$ is near $0$ and $k$ is any number, is given by $y=1+kx$ .

Does it seem reasonable that if a first degree polynomial approximates a differentiable function in an interval near $x_{0}$ , a higher-degree polynomial should approximate the function over a wider interval? Explain your reasoning.

Answers will vary.

Why does a function need to be differentiable at $x_{0}$ for a linear approximation to be used?

Newton’s Method Suppose you use Newton’s Method to solve $f( x) =0$ for a differentiable function $f,$ and you obtain $x_{n+1}=x_{n}.$ What can you conclude?

See Student Solutions Manual.

When Newton’s Method Fails Verify that the function $f(x)= -x^{3}+ 6x^{2}-9x+6$ has a zero in the interval $(2,5)$ . Show that Newton’s Method fails if an initial estimate of $c_{1}=2.9$ is chosen. Repeat Newton’s Method with an initial estimate of $c_{1}=3.0$ . Explain what occurs for each of these two choices. (The zero is near $x=4.2$ .)

When Newton’s Method Fails Show that Newton’s Method fails if it is applied to $f(x)=x^{3}-2x+2$ with an initial estimate of $c_{1}=0$ .

See Student Solutions Manual.

When Newton’s Method Fails Show that Newton’s Method fails if $f(x)=x^{8}-1$ if an initial estimate of $c_{1}=0.1$ is chosen. Explain what occurs.

When Newton’s Method Fails Show that Newton’s Method fails if it is applied to $f(x)=(x-1)^{1/3}$ with an initial estimate of $c_{1}=2$ .

See Student Solutions Manual.

Newton’s Method
1. Use the Intermediate Value Theorem to show that $f( x) =x^{4}+2x^{3}-2x-2$ has a zero in the interval $( -2,-1) .$
2. Use Newton’s Method to find $c_{3},$ a third approximation to the zero from (a).
3. Explain why the initial approximation, $c_{1}=-1$ , cannot be used in (b).

Challenge Problems

Specific Gravity A solid wooden sphere of diameter $d$ and specific gravity $S$ sinks in water to a depth $h$ , which is determined by the equation $2x^{3}-3x^{2}-S=0$ , where $x=\dfrac{h}{d}$ . Use Newton’s Method to find a third approximation to $h$ for a maple ball of diameter 6 in. for which $S=0.786$ .

9.871 in

Kepler’s Equation The equation $x-p\sin x=M$ , called Kepler’s equation, occurs in astronomy. Use Newton’s Method to find a second approximation to $x$ when $p=0.2$ and $M=0.85$ . Use $c_{1}=1$ as your first approximation.

3.4 Assess Your UnderstandingPrinted Page 237

3.4 Assess Your Understanding
Printed Page 237