Question

True or False \(\dfrac{f(x) }{g(x) }\) is an indeterminate form at \(c\) of the type \(\dfrac{0}{0}\) if \(\lim\limits_{x\rightarrow c}\dfrac{f(x) }{g(x) }\) does not exist.

Question

True or False If \(\dfrac{f(x) }{g(x) }\) is an indeterminate form at \(c\) of the type \(\dfrac{0}{0},\) then L’Hôpital’s Rule states that \(\lim\limits_{x\rightarrow c}\dfrac{f(x) }{g(x) }= \lim\limits_{x\rightarrow c}\left[ \dfrac{d}{dx}\left( \dfrac{f(x) }{g(x) }\right) \right]\).

Question

True or False \(\dfrac{1}{x}\) is an indeterminate form at \(0\).

Question

True or False \(x\ln x\) is not an indeterminate form at \(0^{+}\) because \(\lim\limits_{x\rightarrow 0^{+}}x=0\) and \(\lim\limits_{x\rightarrow 0^{+}}\ln x=-\infty\), and \(0\cdot -\infty =0\).

Question

In your own words, explain why \(\infty -\infty \) is an indeterminate form, but \(\infty +\infty \) is not an indeterminate form.

Question

In your own words, explain why \(0\cdot \infty \neq 0.\)

Question

\(\dfrac{1-e^{x}}{x}, \) \(c=0\)

Question

\(\dfrac{1-e^{x}}{x-1}\), \(c=0\)

Question

\(\dfrac{e^{x}}{x}\), \(c=0\)

Question

\(\dfrac{e^{x}}{x},\) \(c=\infty \)

Question

\(\dfrac{\ln x}{x^{2}}\), \(c=\infty \)

Question

\(\dfrac{\ln ( x+1) }{e^{x}-1},\) \(c=0\)

Question

\(\dfrac{\sec x}{x},\)\(c=0\)

Question

\(\dfrac{x}{\sec x-1},\) \(c=0\)

Question

\(\dfrac{\sin x( 1-\cos x) }{x^{2}},\) \(c=0\)

Question

\(\dfrac{\sin x-1}{\cos x}\), \(c=\dfrac{\pi }{2}\)

Question

\(\dfrac{\tan x-1}{\sin ( 4x-\pi ) },\) \(c=\dfrac{\pi }{4}\)

Question

\(\dfrac{e^{x}-e^{-x}}{1-\cos x},\)\(c=0\)

Question

\(x^{2}e^{-x},\) \(c=\infty \)

Question

\(x\;\cot\;x,\) \(c=0\)

Question

\(\csc \dfrac{x}{2}-\cot \dfrac{x}{2},\) \(c=0\)

Question

\( \dfrac{x}{x-1}+\dfrac{1}{\ln x},\) \(c=1\)

Question

\(\left( \dfrac{1}{x^{2}}\right) ^{\sin x},\) \(c=0\)

Question

\((e^{x}+x)^{1/x},\) \(c=0\)

Question

\(( x^{2}-1) ^{x},\) \(c=0\)

Question

\(( \sin x) ^{x},\) \(c=0\)

Question

\(\lim\limits_{x\rightarrow 2}\dfrac{x^{2}+x-6}{x^{2}-3x+2}\)

Question

\(\lim\limits_{x\rightarrow 1}\dfrac{2x^{3}+5x^{2}-4x-3}{x^{3}+x^{2}-10x+8}\)

Question

\(\lim\limits_{x\rightarrow 1}\dfrac{\ln x}{x^{2}-1}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\ln (1-x)}{e^{x}-1}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{e^{x}-e^{-x}}{\sin x}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\tan (2x) }{\ln (1+x)}\)

Question

\(\lim\limits_{x\rightarrow 1}\dfrac{\sin ( \pi x) }{x-1}\)

Question

\(\lim\limits_{x\rightarrow \pi }\dfrac{1+\cos x}{\sin (2x) }\)

Question

\(\lim\limits_{x\rightarrow \infty }\dfrac{x^{2}}{e^{x}}\)

Question

\(\lim\limits_{x\rightarrow \infty } \dfrac{e^{x}}{x^{4}}\)

Question

\(\lim\limits_{x\rightarrow \infty }\dfrac{\ln x}{e^{x}}\)

Question

\(\lim\limits_{x\rightarrow \infty }\dfrac{x+\ln x}{x\ln x}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{e^{x}-1-\!\sin x}{1-\cos x}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{e^{x}-e^{-x}-2\;\sin\;x}{3x^{3}}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\sin x-x}{x^{3}}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{x^{3}}{\cos x-1}\)

Question

\(\lim\limits_{x\rightarrow 0^{+}}(x^{2}\;\ln\;x)\)

Question

\(\lim\limits_{x\rightarrow \infty }(xe^{-x})\)

Question

\(\lim\limits_{x\rightarrow \infty} [x(e^{1/x}-1)]\)

Question

\(\lim\limits_{x\rightarrow \pi /2} [ (1-\!\sin x)\tan x]\)

Question

\(\lim\limits_{x\rightarrow \pi /2}(\sec x-\tan x)\)

Question

\(\lim\limits_{x\rightarrow 0}\left( \cot x-\dfrac{1}{x}\right)\)

Question

\(\lim\limits_{x\rightarrow 1}\left( \dfrac{1}{\ln x}-\dfrac{x}{\ln x}\right)\)

Question

\(\lim\limits_{x\rightarrow 0}\left( \dfrac{1}{x}-\dfrac{1}{e^{x}-1}\right) \)

Question

\(\lim\limits_{x\rightarrow 0^{+}}(2x)^{3x}\)

Question

\(\lim\limits_{x\rightarrow 0^{+}}x^{x^{2}}\)

Question

\(\lim\limits_{x\rightarrow \infty }( x+1)^{e^{-x}}\)

Question

\(\lim\limits_{x\rightarrow \infty }(1+x^{2})^{1/x}\)

Question

\(\lim\limits_{x\rightarrow 0^{+}}(\csc x)^{\sin x}\)

Question

\(\lim\limits_{x\rightarrow \infty }x^{1/x}\)

Question

\(\lim\limits_{x\rightarrow \pi /2^{-}}(\sin x)^{\tan x}\)

Question

\(\lim\limits_{x\rightarrow 0}(\cos x)^{1/x}\)

Question

\(\lim\limits_{x\rightarrow 0^{+}}\dfrac{\cot x}{\cot (2x) }\)

Question

\(\lim\limits_{x\rightarrow \,\infty }\dfrac{\ln (\ln x)}{\ln x}\)

Question

\(\lim\limits_{x\rightarrow 1/2^{-}}\dfrac{\ln (1-2x)}{\tan ( \pi x) }\)

Question

\(\lim\limits_{x\rightarrow 1^{-}}\dfrac{\ln (1-x)}{\cot ( \pi x) } \)

Question

\(\lim\limits_{x\rightarrow \infty }\dfrac{x^{4}+x^{3}}{e^{x}+1}\)

Question

\(\lim\limits_{x\rightarrow \infty }\dfrac{x^{2}+x-1}{e^{x}+ e^{-x}}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{xe^{4x}-x}{1-\cos (2x) }\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{x\tan x}{1-\cos x}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\tan ^{-1}x}{x}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\tan ^{-1}x}{\sin ^{-1}x}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\cos x-1}{\cos (2x) -1}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\tan x-\!\sin x}{x^{3}}\)

Question

\(\lim\limits_{x\rightarrow 0^{+}}(x^{1/2} \ \ln x)\)

Question

\(\lim\limits_{x\rightarrow \infty } [ (x-1)e^{-x^{2}}]\)

Question

\(\lim\limits_{x\rightarrow \pi /2} [ \tan x \ \ln (\sin x) ] \)

Question

\(\lim\limits_{x\rightarrow 0^{+}}[ \sin x \ \ln (\sin x)] \)

Question

\(\lim\limits_{x\rightarrow 0}\ [ \csc x \ \ln (x+1)] \)

Question

\(\lim\limits_{x\rightarrow \pi /4}[(1-\tan x) \ \sec (2x) ]\)

Question

\(\lim\limits_{x\rightarrow a}\left[ (a^{2}-x^{2}) \ \tan \left( \dfrac{\pi x}{2a}\right) \right] \)

Question

\(\lim\limits_{x\rightarrow 1^{+}}\,\left[ (1-x)\tan \!\left(\!\dfrac{1}{2}\pi x\!\right)\! \right]\)

Question

\(\lim\limits_{x\rightarrow 1}\left( \dfrac{1}{\ln x}-\dfrac{1}{x-1}\right)\)

Question

\(\lim\limits_{x\rightarrow 1}\left(\! \dfrac{x}{x-1}-\dfrac{1}{\ln x}\! \right)\)

Question

\(\lim\limits_{x\rightarrow \pi /2}\left( x\;\tan\;x-\dfrac{\pi }{2}\sec x\right)\)

Question

\(\lim\limits_{x\rightarrow \pi }(\cot\;x-x\;\csc\;x) \)

Question

\(\lim\limits_{x\rightarrow 1^{-}}(1-x)^{\tan\;( \pi x) }\)

Question

\(\lim\limits_{x\rightarrow 0^{+}}x^{\sqrt{\scriptstyle x}}\)

Question

\(\lim\limits_{x\rightarrow 0}\left( \dfrac{\sin\;x}{x}\right) ^{\!\!1/x}\)

Question

\(\lim\limits_{x\rightarrow \infty }\left(\! 1+\dfrac{5}{x}+\dfrac{3}{x^{2}}\!\right) ^{\!\!x}\)

Question

\(\lim\limits_{x\rightarrow ( \pi /2) ^{-}}( \tan x) ^{\cos x}\)

Question

\(\lim\limits_{x\rightarrow 0^{+}}( x^{2}+x) ^{-\ln x}\)

Question

\(\lim\limits_{x\rightarrow 0}( \cosh x) ^{e^{x}}\)

Question

\(\lim\limits_{x\rightarrow 0^{+}}(\sinh x) ^{x}\)

Question

Wolf Population In 2002 there were \(65\) wolves in Wyoming outside of Yellowstone National Park, and in 2010 there were \(247\) wolves. Suppose the population \(w\) of wolves in the region at time \(t\) follows the logistic growth curve \[ w=w(t)=\dfrac{Ke^{rt}}{\dfrac{K}{40}+e^{rt}-1} \]

where \(K=366\), \(r=0.283\), and \(t=0\) represents the population in the year 2000.

1. Find \(\lim\limits_{t\rightarrow \infty }w(t).\)
2. Interpret the answer found in (a).
3. Use graphing technology to graph \(w=w(t)\).

Question

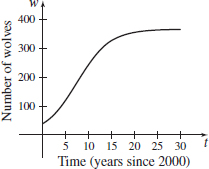
Skydiving The downward velocity \(v\) of a skydiver with nonlinear air resistance can be modeled by \[ v=v(t) =-A+RA\frac{e^{Bt+C}-1}{e^{Bt+C}+1} \]

where \(t\) is the time in seconds, and \(A,B,C,\) and \(R\) are positive constants with \(R>1\).

1. Find \(\lim\limits_{t\rightarrow \infty }v(t) \).
2. Interpret the limit found in (a).
3. If the velocity \(v\) is measured in feet per second, reasonable values of the constants are \(A=108.6,\) \(B=0.554\), \(C=0.804,\) and \(R=2.62.\) Graph the velocity of the skydiver with respect to time.

Question

Electricity  The equation governing the amount of current \(I\) (in amperes) in a simple RL circuit consisting of a resistance \(R\) (in ohms), an inductance \(L\) (in henrys), and an electromotive force \(E\) (in volts) is \(\ I=\dfrac{E}{R}( 1-e^{-Rt/L}) \).

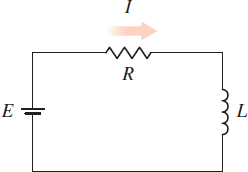
1. Find \(\lim\limits_{t\rightarrow \infty }I(t)\) and \(\lim\limits_{R\rightarrow 0^{+}}I(t)\).
2. Interpret these limits.

Question

Find \(\lim\limits_{x\rightarrow 0}\dfrac{a^{x}-b^{x}}{x},\) where \(a\neq 1\) and \(b\neq 1\) are positive real numbers.

Question

Show that \(\lim\limits_{x\,\rightarrow \,\infty } \frac{\ln x}{x^{n}}=0\), for \(n \ge 1\) an integer.

Question

Show that \(\lim\limits_{x\rightarrow \,\infty } \frac{x^{n}}{e^{x}}=0\) for \(n \ge 1\) an integer.

Question

Show that \(\lim\limits_{x\rightarrow 0^{+}}(\cos\;x+2\;\sin x)^{\cot\;x}=e^{2}\).

Question

Find \(\lim\limits_{x\rightarrow \,\infty } \dfrac{P(x)}{e^{x}}\), where \(P\) is a polynomial function.

Question

Find \(\lim\limits_{x\rightarrow \infty }\left[ \ln (x+1)-\ln (x-1)\right] .\)

Question

Show that \(\lim\limits_{x\rightarrow 0^{+}}\dfrac{e^{-1/x^{2}}}{x}=0\). Hint: Write \(\dfrac{e^{-1/x^{2}}}{x}=\dfrac{\dfrac{1}{x}}{e^{1/x^{2}}}.\)

Question

If \(n\) is an integer, show that \(\lim\limits_{x\rightarrow 0^{+}}\dfrac{e^{-1/x^{2}}}{x^{n}}=0\).

Question

Show that \(\lim\limits_{x\rightarrow \infty }\sqrt[x]{x}=1.\)

Question

Show that \(\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{a}{x}\right) ^{\!\!x}=e^{a},\) \(a\) any real number.

Question

Show that \(\lim\limits_{x\rightarrow \infty }\left( \dfrac{x+a}{x-a}\right) ^{\!\!x}= e^{2a}, a\ne 0\).

Question

1. Show that the function below has a derivative at \(0\). What is \(f^{\prime }(0)\)? \[ f(x)= \left\{ \begin{array}{l{\qquad}l{\quad}rcl} e^{-1/x^{2}} & \hbox{if} & x&\neq& 0 \\ 0 & \hbox{if} & x&=&0 \end{array} \right. \]
2. Graph \(f\) using a graphing utility.

Question

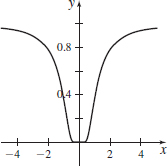
If \(a,b\neq 0\) and \(c>0\) are real numbers, show that \[ \lim\limits_{x\rightarrow c}\dfrac{x^{a}-c^{a}}{x^{b}-c^{b}}=\dfrac{a}{b} c^{a-b}. \]

Question

Prove L’Hôpital’s rule when \(\dfrac{f(x)}{g(x) }\) is an indeterminate form at \(-\infty \) of the type \(\dfrac{0}{0}\).

Question

Explain why L’Hôpital’s Rule does not apply to \(\lim\limits_{x\rightarrow 0}\dfrac{x^{2}\sin \dfrac{1}{x}}{\sin x}.\)

Question

Find each limit:

1. \(\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{x }\right) ^{\!\!\!-x^{2}}\)
2. \(\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{\ln a}{x}\right) ^{\!\!x},\) \(a>1\)
3. \(\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{x}\right) ^{\!\!x^{2}} \)
4. \(\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{\sin x}{x}\right) ^{\!\!x}\)
5. \(\lim\limits_{x\rightarrow \infty }( e^{x}) ^{-1/\ln x}\)
6. \(\lim\limits_{x\rightarrow \infty } \) \(\left[ \left( \dfrac{1}{a}\right) ^{\!\!x}\right] ^{-1/x},\) \(0<a<1\)
7. \(\lim\limits_{x\rightarrow \infty }x^{1/x}\)
8. \(\lim\limits_{x\rightarrow \infty }( a^{x}) ^{1/x},\) \(a>1\)
9. \(\lim\limits_{x\rightarrow \infty } [ (2+\sin x) ^{x}] ^{1/x}\)
10. \(\lim\limits_{x\rightarrow0^{+}}x^{-1/\ln x}\)

Question

Find constants \(A,\) \(B\), \(C\), and \(D\) so that \[ \lim\limits_{x\rightarrow 0}\dfrac{\sin ( Ax) +Bx+Cx^{2}+Dx^{3}}{x^{5}}=\dfrac{4}{15}. \]

Question

A function \(f\) has derivatives of all orders.

1. Find \(\lim\limits_{h\rightarrow 0}\dfrac{f(x+2h)-2\,f(x+h)+f(x)}{h^{2}}\).
2. Find \(\lim\limits_{h\rightarrow 0}\dfrac{f(x+3h)-3\,f(x+2h)+3\,f(x+h)-f(x)}{h^{3}}\).
3. Generalize parts (a) and (b).

Question

The formulas in Problem 111 can be used to approximate derivatives. Approximate \(f^\prime (2),\) \(\ f^{\prime \prime} (2)\), and \( f’’’ (2)\) from the table. The data are for \(f(x)=\ln x\). Compare the exact values with your approximations.

Question

Consider the function \(f( t,x) =\dfrac{x^{t+1}-1}{t+1},\) where \(x>0\) and \(t\neq -1.\)

1. For \(x\) fixed at \(x_{0},\) show that \(\lim\limits_{t\rightarrow -1}f( t,x_0) =\ln\;x_{0}\).
2. For \(x\) fixed, define a function \(F( t,x) ,\) where \(x>0,\) that is continuous so \(F( t,x) =f( t,x) \) for all \(t\neq -1\).
3. For \(t\) fixed, show that \(\dfrac{d}{dx}F( t,x) =x^{t},\) for \(x>0\) and all \(t.\)