4.2 Assess Your UnderstandingPrinted Page 272
Concepts and Vocabulary
True or False Any function f that is defined on a closed interval [a,b] will have both an absolute maximum value and an absolute minimum value.
False
Multiple Choice A number c in the domain of a function f is called a(n) [(a) extreme value, (b) critical number, (c) local number] of f if either f′(c)=0 or f′(c) does not exist.
(b)
True or False At a critical number, there is a local extreme value.
False
True or False If a function f is continuous on a closed interval [a,b] , then its absolute maximum value is found at a critical number.
False
True or False The Extreme Value Theorem tells us where the absolute maximum and absolute minimum can be found.
False
True or False If f is differentiable on the interval (0,4) and f′(2)=0, then f has a local maximum or a local minimum at 2.
False
Skill Building
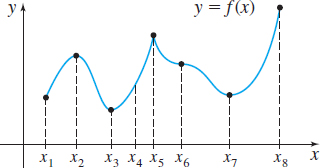
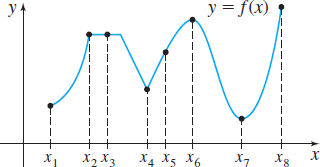
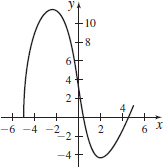
In Problems 7 and 8, use the graphs below to determine whether the function f has an absolute extremum and/or a local extremum or neither at x1, x2, x3, x4, x5, x6, x7, and x8.
x1: neither, x2: local maximum, x3: local minimum and absolute minimum, x4: neither, x5: local maximum, x6: neither, x7: local minimum, x8: absolute maximum
In Problems 9–12, provide a graph of a continuous function f that has the following properties:
domain [0,8], absolute maximum at 0, absolute minimum at 3, local minimum at 7.
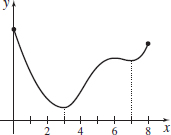
domain [−5,5], absolute maximum at 3, absolute minimum at −3.
domain [3,10] and has no local extreme points.

no absolute extreme values, is differentiable at 4 and has a local minimum at 4, is not differentiable at 0, but has a local maximum at 0.
In Problems 13–36, find the critical numbers, if any, of each function.
f(x)=x2−8x
4
f(x)=1−6x+x2
f(x)=x3−3x2
0, 2
f(x)=x3−6x
f(x)=x4−2x2+1
−1, 0, 1
f(x)=3x4−4x3
f(x)=x2/3
0
f(x)=x1/3
f(x)=2√x
0
f(x)=4−√x
f(x)=x+sinx, 0≤x≤π
π
f(x)=x−cosx, −π2≤x≤π2
273
f(x)=x√1−x2
−√22, −1, 1, √22
f(x)=x2√2−x
f(x)=x2x−1
0, 2
f(x)=xx2−1
f(x)=(x+3)2(x−1)2/3
−3, 0, 1
f(x)=(x−1)2(x+1)1/3
f(x)=(x−3)1/3x−1
3, 4
f(x)=(x+3)2/3x+1
f(x)=3√x2−9x
−3√3, −3, 3, 3√3
f(x)=3√4−x2x
f(x)={3xif0≤x<14−xif1≤x≤2
1
f(x)={x2if0≤x<11−x2if1≤x≤2
In Problems 37–64, find the absolute maximum value and absolute minimum value of each function on the indicated interval. Notice that the functions in Problems 37–58 are the same as those in Problems 13–34.
f(x)=x2−8x on [−1,10]
Absolute maximum 20 at x=10, absolute minimum −16 at x=4
f(x)=1−6x+x2 on [0,4]
f(x)=x3−3x2 on [1,4]
Absolute maximum 16 at x=4, absolute minimum −4 at x=2
f(x)=x3−6x on [−1,1]
f(x)=x4−2x2+1 on [0,2]
Absolute maximum 9 at x=2, absolute minimum 0 at x=1
f(x)=3x4−4x3 on [−2,0]
f(x)=x2/3 on [−1,1]
Absolute maximum 1 at x=−1,1, absolute minimum 0 at x=0
f(x)=x1/3 on [−1,1]
f(x)=2√x on [1,4]
Absolute maximum 4 at x=4, absolute minimum 2 at x=1
f(x)=4−√x on [0,4]
f(x)=x+sinx on [0,π]
Absolute maximum π at x=π, absolute minimum 0 at x=0
f(x)=x−cosx on [−π2,π2]
f(x)=x√1−x2 on [−1,1]
Absolute maximum 12 at x=√22, absolute minimum −12 at x=−√22
f(x)=x2√2−x on [0,2]
f(x)=x2x−1 on [−1,12]
Absolute maximum 0 at x=0, absolute minimum −12 at x=−1,12
f(x)=xx2−1 on [−12,12]
f(x)=(x+3)2(x−1)2/3 on [−4,5]
Absolute maximum 643√16 at x=5, absolute minimum 0 at x=−3,1
f(x)=(x−1)2(x+1)1/3 on [−2,7]
f(x)=(x−3)1/3x−1 on [2,11]
Absolute maximum 13 at x=4, absolute minimum −1 at x=2
f(x)=(x+3)2/3x+1 on [−4,−2]
f(x)=3√x2−9x on [3,6]
Absolute maximum 3√183√3 at x=3√3, absolute minimum 0 at x=3
f(x)=3√4−x2x, on [−4,−1]
f(x)=ex−3x on [0,1]
Absolute maximum 1 at x=0, absolute minimum e−3 at x=1
f(x)=ecosx on [−π,2π].
f(x)={2x+1if0≤x<13xif1≤x≤3
Absolute maximum 9 at x=3, absolute minimum 1 at x=0
f(x)={x+3if −1≤x≤22x+1if 2<x≤4
f(x)={x2if −2≤x<1x3if 1≤x≤2
Absolute maximum 8 at x=2, absolute minimum 0 at x=0
f(x)={x+2if −1≤x<02−xif 0≤x≤1
Applications and Extensions
In Problems 65–68, for each function f:
- (a) Find the derivative f′.
- (b)
 Use technology to find the critical numbers of f.
Use technology to find the critical numbers of f.
- (c)
 Graph f and describe the behavior of f suggested by the graph at each critical number.
Graph f and describe the behavior of f suggested by the graph at each critical number.
f(x)=3x4−2x3−21x2+36x
- (a) f′(x)=12x3−6x2−42x+36
- (b) −2, 1, 32
- (c) Absolute minimum at x=−2, local maximum at x=1, local minimum at x=32
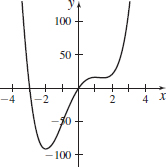
f(x)=x2+2x−2x
f(x)=(x2−5x+2)√x+5√x2+2
- (a) f′(x)= 3x4+5x3+8x2−10x−962√x+5(x2+2)32
- (b) −5,≈−2.364, ≈1.977
- (c) Local maximum at x≈−2.364, local minimum at x≈1.977, neither a local minimum nor a local maximum at x=−5.
f(x)=(x2−9x+16)√x+3√x2−4x+6
In Problems 69 and 70, for each function f:
- (a) Find the derivative f′.
- (b)
 Use technology to find the absolute maximum value and the absolute minimum value of f on the closed interval [0,5].
Use technology to find the absolute maximum value and the absolute minimum value of f on the closed interval [0,5].
- (c) Graph f. Are the results from (b) supported by the graph?
f(x)=x4−12.4x3+49.24x2−68.64x
- (a) f′(x)=4x3−37.2x2+98.48x−68.64
- (b) Absolute maximum 0 at x=0, absolute minimum −37.2 at x=5
- (c)

f(x)=e−xsin(2x)+e−x/2cos(2x)
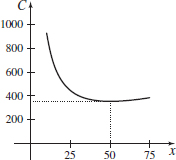
Cost of Fuel A truck has a top speed of 75mi/h, and when traveling at the rate of xmi/h, it consumes fuel at the rate of 1200(2500x+x) gallon per mile. If the price of fuel is $3.60/gal, the cost C (in dollars) of driving 200mi is given by C(x)=(3.60)(2500x+x)
- (a) What is the most economical speed for the truck to travel? Use the interval [10,75].
- (b)
 Graph the cost function C.
Graph the cost function C.
- (a) 50 mi/h
- (b)
274
Trucking Costs If the driver of the truck in Problem 71 is paid $28.00 per hour and wages are added to the cost of fuel, what is the most economical speed for the truck to travel?
Projectile Motion An object is propelled upward at an angle θ, 45∘ <θ <90∘, to the horizontal with an initial velocity of v0 ft/s from the base of an inclined plane that makes an angle of 45∘ to the horizontal. See the illustration below. If air resistance is ignored, the distance R that the object travels up the inclined plane is given by the function R(θ)=v20√216cosθ(sinθ−cosθ)
- (a) Find the angle θ that maximizes R. What is the maximum value of R?
- (b)
 Graph R=R(θ), 45∘≤θ≤90∘, using v0=32 \,{\rm ft}/{\rm s}\).
Graph R=R(θ), 45∘≤θ≤90∘, using v0=32 \,{\rm ft}/{\rm s}\). - (c) Does the graph support the result from (a)?
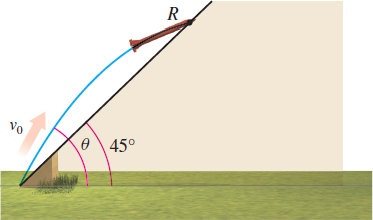
- (a) 67.5∘, 0.0183v20 ft
- (b)

- (c) Answers will vary.
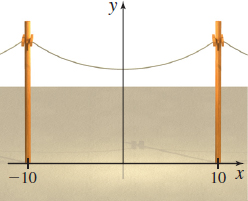
Height of a Cable An electric cable is suspended between two poles of equal height that are 20m apart, as illustrated in the figure. The shape of the cable is modeled by the equation y=10coshx10+15. If the x-axis is placed along the ground and the two poles are at (−10,0) and (10,0) , what is the height of the cable at its lowest point?
A Record Golf Stroke The fastest golf ball speed ever recorded, 91.1m/s (204mi/h!), was a ball hit by Jason Zuback in 2007. When a ball is hit at an angle θ to the horizontal, 0∘≤θ≤90∘, and lands at the same level from which it was hit, the horizontal range R of the ball is given by R=2v20gsinθcosθ , where v0 is the initial speed of the ball and g=9.8m/s2 is the acceleration due to gravity.
- (a) Show that the golf ball achieves its maximum range if the golfer hits it at an angle of 45∘.
- (b) What is the maximum range that could be achieved by the record golf ball speed?
- (a) See Student Solutions Manual.
- (b) ≈846.858 m
Optics When light goes through a thin slit, it spreads out (diffracts). After passing through the slit, the intensity I of the light on a distant screen is given by I=I0(sinαα)2, where I0 is the original intensity of the light and α depends on the angle away from the center.
- (a) What is the intensity of the light as α→0?
- (b) Show that the bright spots, that is, the places where the intensity has a local maximum, occur when tanα=α.
- (c) Is the intensity of the light the same at each bright spot?
Economics In Problems 77 and 78, use the following discussion:
In determining a tax rate on consumer goods, the government is always faced with the question, "What tax rate produces the largest tax revenue?" Imposing a tax may cause the price of the goods to increase and reduce the demand for the product. A very large tax may reduce the demand to zero, with the result that no tax is collected. On the other hand, if no tax is levied, there is no tax revenue at all. (Tax revenue R is the product of the tax rate t times the actual quantity q, in dollars, consumed.)
The government has determined that the relationship between the quantity q of a product consumed and the related tax rate t is t=√27−3q2. Find the tax rate that maximizes tax revenue. How much tax is generated by this rate?
A tax rate of 3√62≈3.674 maximizes revenue. The maximum revenue generated is 9√32≈7.794
On a particular product, government economists determine that the relationship between the tax rate t and the quantity q consumed is t+3q2=18. Find the tax rate that maximizes tax revenue and the revenue generated by the tax.
Catenary A town hangs strings of holiday lights across the road between utility poles. Each set of poles is 12m apart. The strings hang in catenaries modeled by y=15coshx15−10 with the poles at (±6,0). What is the height of the string of lights at its lowest point?
5 m
Harmonic Motion An object of mass 1kg moves in simple harmonic motion, with an amplitude A=0.24m and a period of 4 seconds. The position s of the object is given by s(t)=Acos(ωt), where t is the time in seconds.
- (a) Find the position of the object at time t and at time t=0.5 seconds.
- (b) Find the velocity v=v(t) of the object.
- (c) Find the velocity of the object when t=0.5 seconds.
- (d) Find the acceleration a=a(t) of the object.
- (e) Use Newton’s Second Law of Motion, F=ma, to find the magnitude and direction of the force acting on the object when t=0.5 second.
- (f) Find the minimum time required for the object to move from its initial position to the point where s=−0.12m.
- (g) Find the velocity of the object when s=−0.12m.

- (a) Find the critical numbers of f(x)=x33−0.055x2+0.0028x−4.
- (b) Find the absolute extrema of f on the interval [−1,1].
- (c) Graph f on the interval [−1,1].
- (a) 0.04, 0.07
- (b) Absolute maximum −3.719 at x=1, absolute minimum −4.391 at x=−1
- (c)

275
 Extreme Value
Extreme Value- (a) Find the minimum value of y=x−cosh−1x.
- (b) Graph y=x−cosh−1x.
Locating Extreme Values Find the absolute maximum value and the absolute minimum value of f(x)=√1+x2+|x−2| on [0,3], and determine where each occurs.
Absolute maximum √10+1 at x=3, absolute minimum √5 at x=2
The function f(x)=Ax2+Bx+C has a local minimum at 0, and its graph contains the points (0,2) and (1,8). Find A, B, and C.
- (a) Determine the domain of the function f(x)=[(16−x2)(x2−9)]1/2.
- (b) Find the absolute maximum value of f on its domain.
- (a) [−4,−3]∪[3,4]
- (b) 72
Absolute Extreme Values Without finding them, explain why the function f(x)=√x(2−x) must have an absolute maximum value and an absolute minimum value. Then find the absolute extreme values in two ways (one with and one without calculus).
Put It Together If a function f is continuous on the closed interval [a,b], which of the following is necessarily true?
- (a) f is differentiable on the open interval (a,b).
- (b) If f(u) is an absolute maximum value of f, then f′(u)=0.
- (c) lim for a<c<b.
- (d) f^\prime (x)=0, for some x, a\leq x\leq b.
- (e) f has an absolute maximum value on [a,b] .
(c) (e)
Write a paragraph that explains the similarities and differences between an absolute extreme value and a local extreme value.
Explain in your own words the method for finding the absolute extreme values of a continuous function that is defined on a closed interval.
See Student Solutions Manual.
A function f is defined and continuous on the closed interval [ a,b] . Why can’t f(a) be a local extreme value on [ a,b] ?
Show that if f has a local minimum at c, then g(x) = -f(x) has a local maximum at c.
See Student Solutions Manual.
Show that if f has a local minimum at c, then either f^\prime (c) = 0 or f^\prime (c) does not exist.
Challenge Problem
- (a) Prove that a rational function of the form f(x)=\dfrac{ax^{2n}+b}{cx^{n}+d}, n\geq 1 an integer, has at most five critical numbers.
- (b) Give an example of such a rational function with exactly five critical numbers.
- (a) See Student Solutions Manual.
- (b) Answers will vary.