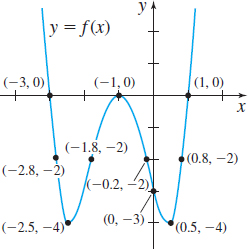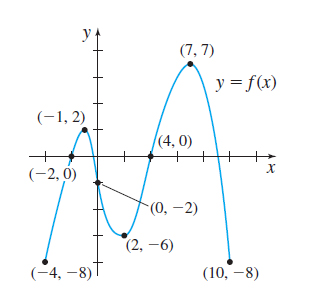4.4 Assess Your UnderstandingPrinted Page 294
Concepts and Vocabulary
True or False If a function f is continuous on the interval [a,b], differentiable on the interval (a,b), and changes from an increasing function to a decreasing function at the point (c,f(c)), then (c,f(c)) is an inflection point of f.
False
True or False Suppose c is a critical number of f and (a,b) is an open interval containing c. If f′(x) is positive on both sides of c, then f(c) is a local maximum value.
False
Multiple Choice Suppose a function f is continuous on a closed interval [a,b] and differentiable on the open interval (a,b). If the graph of f lies above each of its tangent lines on the interval (a,b), then f is [(a) concave up, (b) concave down, (c) neither] on (a,b).
(a)
Multiple Choice If the acceleration of an object in rectilinear motion is negative, then the velocity of the object is [(a) increasing, (b) decreasing, (c) neither].
(b)
Multiple Choice Suppose f is a function that is differentiable on an open interval containing c and the concavity of f changes at the point (c,f(c)). Then (c,f(c)) is a(n) [(a) inflection point, (b) critical point, (c) both (d) neither] of f.
(a)
Multiple Choice Suppose a function f is continuous on a closed interval [a,b] and both f′ and f′′ exist on the open interval (a,b). If f′′(x)>0 on the interval (a,b), then f is [(a) increasing, (b) decreasing, (c) concave up, (d) concave down] on (a,b).
(c)
True or False Suppose f is a function for which f′ and f′′ exist on an open interval (a,b) and suppose c, a<c<b, is a critical number of f. If f′′(c)=0, then the Second Derivative Test cannot be used to determine if there is a local extremum at c.
True
True or False Suppose a function f is differentiable on the open interval (a,b). If either f′′(c)=0 or f′′ does not exist at the number c in (a,b), then (c,f(c)) is an inflection point of f.
False
Skill Building
In Problems 9–12, the graph of a function f is given.
- (a) Identify the points where each function has a local maximum value, a local minimum value, or an inflection point.
- (b) Identify the intervals on which each function is increasing, decreasing, concave up, or concave down.
- (a) Local maximum at (−1,0), local minimum at (−2.5,−4) and (0.5,−4), inflection points (−1.8,−2) and (−0.2,−2)
- (b) Increasing on [−2.5,−1]∪[0.5,∞), decreasing on (−∞,−2.5]∪[−1,0.5], concave up on (−∞,−1.8)∪(−0.2,∞), concave down on (−1.8,−0.2)
- (a) Local maximum at (−2,3) and (12,10), local minimum at (0,0), no inflection point
- (b) Increasing on (−∞,−2]∪[0,12], decreasing on [−2,0]∪[12,∞), never concave up, concave down on (−∞,0)∪(0,∞)
In Problems 13–30, for each function:
- (a) Find the critical numbers.
- (b) Use the First Derivative Test to find any local extrema.
f(x)=x3−6x2+2
- (a) 0, 4
- (b) Local maximum 2 at 0, local minimum −30 at 4
f(x)=x3+6x2+12x+1
295
f(x)=3x4−4x3
- (a) 0, 1
- (b) Local minimum −1 at 1
h(x)=x4+2x3−3
f(x)=(5−2x)ex
- (a) 32
- (b) Local maximum 2e32 at 32
f(x)=(x−8)ex
g(u)=u−1eu
- (a) 1
- (b) Local minimum e at 1
f(x)=x−2ex
f(x)=x2/3+x1/3
- (a) −18, 0
- (b) Local minimum −14 at −18
f(x)=12x2/3−x1/3
g(x)=x2/3(x2−4)
- (a) −1, 0, 1
- (b) Local maximum 0 at 0, local minimum −3 at −1 and 1
f(x)=x1/3(x2−9)
f(x)=lnxx3
- (a) 3√e
- (b) Local maximum 13e at 3√e
h(x)=lnx√x3
g(x)=|x2−1|
- (a) −1, 0, 1
- (b) Local maximum 1 at 0, local minimum 0 at −1 and 1
f(x)=|x2−4|
f(θ)=sinθ−2cosθ
- (a) kπ−tan−112, k an integer
- (b) Local maximum √5 at (2k+1)π−tan−112, local minimum −√5 at 2kπ−tan−112
f(x)=x+2sinx
In Problems 31–38, the distance s of an object from the origin at time t≥0 (in seconds) is given. The motion is along a horizontal line with the positive direction to the right.
- (a) Determine the intervals during which the object moves to the right and the intervals during which it moves to the left.
- (b) When does the object reverse direction?
- (c) When is the velocity of the object increasing and when is it decreasing?
- (d) Draw a figure to illustrate the motion of the object.
- (e) Draw a figure to illustrate the velocity of the object.
s=t2−2t+3
- (a) The object moves right on (1,∞), left on (0,1)
- (b) t=1
- (c) The velocity is increasing on (0,∞)
- (d)
- (e)
s=2t2+8t−7
s=2t3+6t2−18t+1
- (a) The object moves right on (1,∞), left on (0,1)
- (b) t=1
- (c) The velocity is increasing on (0,∞)
- (d)
- (e)
s=3t4−16t3+24t2
s=2t−6t,t>0
- (a) The object moves right on (0,∞)
- (b) No direction reverse
- (c) The velocity is decreasing on (0,∞)
- (d)
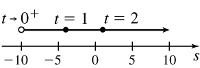
- (e)
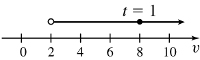
s=3√t−1√t,t>0
s=2sin(3t),0≤t≤2π3
- (a) The object moves right on (0,π6) and (π2,2π3), left on (π6,π2)
- (b) t=π6,π2
- (c) The velocity is increasing on (π3,2π3), decreasing on (0,π3)
- (d)
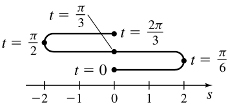
- (e)
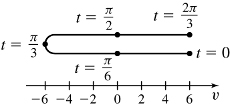
s=3cos(πt),0≤t≤2
In Problems 39–54, (a) determine the intervals on which each function is concave up and on which it is concave down; (b) find any points of inflection.
f(x)=x2−2x+5
- (a) Concave up on (−∞,∞)
- (b) No inflection point
f(x)=x2+4x−2
f(x)=x3−9x2+2
- (a) Concave up on (3,∞), concave down on (−∞,3)
- (b) (3,−52)
f(x)=x3−6x2+9x+1
f(x)=x4−4x3+10
- (a) Concave up on (−∞,0)∪(2,∞), concave down on (0,2)
- (b) (0,10), (2,−6)
f(x)=3x4−8x3+6x+1
f(x)=x2/3ex
- (a) Concave up on (−∞,−2−√63)∪(−2+√63,∞), concave down on (−2−√63,0)∪(0,−2+√63)
- (b) (−1.483,0.295), (0.150,0.328)
f(x)=x2/3e−x
f(x)=lnxx3
- (a) Concave up on (e7/12,∞), concave down on (0,e7/12)
- (b) (e7/12,712e−7/4)
f(x)=lnx√x3
f(x)=x+1x
- (a) Concave up on (0,∞), concave down on (−∞,0)
- (b) No inflection point
f(x)=2x2−1x
f(x)=3x1/3+2x
- (a) Concave up on (−∞,0), concave down on (0,∞)
- (b) (0,0)
f(x)=x4/3−8x1/3
f(x)=3−4x+4x2
- (a) Concave up on (−∞,0)∪(0,3), concave down on (3,∞)
- (b) (3,199)
f(x)=(x−1)3/2
In Problems 55–80:
- (a) Find the local extrema of f.
- (b) Determine the intervals on which f is concave up and on which it is concave down.
- (c) Find any points of inflection.
f(x)=2x3−6x2+6x−3
- (a) No local extrema
- (b) Concave up on (1,∞), concave down on (−∞,1)
- (c) (1,−1)
f(x)=2x3+9x2+12x−4
f(x)=x4−4x
- (a) Local minimum −3 at x=1
- (b) Concave up on (−∞,0)∪(0,∞)
- (c) No inflection point
f(x)=x4+4x
f(x)=5x4−x5
- (a) Local maximum 256 at x=4, local minimum 0 at x=0
- (b) Concave up on (−∞,0)∪(0,3), concave down on (3,∞)
- (c) (3,162)
f(x)=4x6+6x4
f(x)=3x5−20x3
- (a) Local maximum 64 at x=−2, local minimum −64 at x=2
- (b) Concave up on (−√2,0)∪(√2,∞), concave downon (−∞,−√2)∪(0,√2)
- (c) (0,0), (√2,−28√2), (−√2,28√2)
f(x)=3x5+5x3
f(x)=x2ex
- (a) Local maximum 4e−2 at x=−2, local minimum 0 at x=0
- (b) Concave up on (−∞,−2−√2)∪(−2+√2,∞), concave down on (−2−√2,−2+√2)
- (c) (−2−√2,(6+4√2)e−2−√2), (−2+√2,(6−4√2)e−2+√2)
f(x)=x3ex
f(x)=ex+e−x2
- (a) Local minimum 1 at x=0
- (b) Concave up on (−∞,∞)
- (c) No inflection point
f(x)=ex−e−x2
f(x)=6x4/3−3x1/3
- (a) Local minimum −98 at x=18
- (b) Concave up on (−∞,−14)∪(0,∞), concave down on (−14,0)
- (c) (−14,93√24), (0,0)
f(x)=x2/3−x1/3
f(x)=x2/3(x2−8)
- (a) Local maximum 0 at x=0, local minimum −63√2 at x=−√2 and √2
- (b) Concave up on (−∞,0)∪(0,∞)
- (c) No inflection point
f(x)=x1/3(x2−2)
f(x)=x2−lnx
- (a) Local minimum 12+12ln2 at x=√22
- (b) Concave up on (0,∞)
- (c) No inflection point
f(x)=lnx−x
f(x)=x(1+x2)5/2
- (a) Local maximum 16√5125 at x=12, local minimum −16√5125 at x=−12
- (b) Concave up on (−√32,0)∪(√32,∞), concave down on (−∞,−√32)∪(0,√32)
- (c) (−√32,−16√375/2), (√32,16√375/2), (0,0)
f(x)=√x1+x
f(x)=x2√1−x2
- (a) Local maximum 2√39 at x=±√63, local minimum 0 at x=0
- (b) Concave up on (−16√27−3√33,16√27−3√33), concave down on (−1,−16√27−3√33)∪(16√27−3√33,1)
- (c) (±16√27−3√33,9−√3312√3+√3312)
f(x)=x√1−x
f(x)=sin2x
- (a) Local maximum 1 at x=kπ+π2, local minimum 0 at x=kπ, k an integer.
- (b) Concave up on (kπ−π4,kπ+π4), concave down on (kπ+π4,kπ+3π4), k an integer.
- (c) ((2k+1)π4,12), k an integer.
f(x)=cos2x
f(x)=x−2sinx,0≤x≤2π
- (a) Local maximum 5π3+√3 at x=5π3, local minimum π3−√3 at x=π3
- (b) Concave up on (0,π), concave down on (π,2π)
- (c) (π,π)
f(x)=2cos2x−sin2x,0≤x≤2π
In Problems 81–84, find the local extrema of each function f by:
- (a) Using the First Derivative Test.
- (b) Using the Second Derivative Test.
- (c) Discuss which of the two tests you found easier.
f(x)=−2x3+15x2−36x+7
(a) Local maximum −20 at x=3, local minimum −21 at x=2
(b) Same as (a).
(c) Answers will vary
f(x)=x3+10x2+25x−25
f(x)=(x−3)2ex
(a) Local maximum 4e at x=1, local minimum 0 at x=3
(b) Same as (a).
(c) Answers will vary.
f(x)=(x+1)2e−x
Applications and Extensions
In Problems 85–96, sketch the graph of a continuous function f that has the given properties. Answers will vary.
f is concave up on (−∞,∞), increasing on (−∞,0), decreasing on (0,∞), and f(0)=1.
Answers will vary.
f is concave up on (−∞,0), concave down on (0,∞), decreasing on (−∞,0), increasing on (0,∞), and f(0)=1.
f is concave down on (−∞,1), concave up on (1,∞), decreasing on (−∞,0), increasing on (0,∞), f(0)=1, and f(1)=2.
Answers will vary.
f is concave down on (−∞,0), concave up on (0,∞), increasing on (−∞,∞), and f(0)=1 and f(1)=2.
f′(x)>0 if x<0; f′(x)<0 if x>0; f′′(x)>0 if x<0; f′′(x)>0 if x>0 and f(0)=1.
Answers will vary.
f′(x)>0 if x<0; f′(x)<0 if x>0; f′′(x)>0 if x<0; f′′(x)<0 if x>0 and f(0)=1.
f′′(0)=0; f′(0)=0; f′′(x)>0 if x<0; f′′(x)>0 if x>0 and f(0)=1.
Answers will vary.
f′′(0)=0; f′(x)>0 if x≠0; f′′(x)<0 if x<0; f′′(x)>0 if x>0 and f(0)=1.
f′(0)=0; f′(x)<0 if x≠0; f′′(x)>0 if x<0; f′′(x)<0 if x>0; f(0)=1.
Answers will vary.
296
f′′(0)=0; f′(0)=12; f′′(x)>0 if x<0; f′′(x)<0 if x>0 and f(0)=1.
f′(0) does not exist; f′′(x)>0 if x<0; f′′(x)>0 if x>0 and f(0)=1.
Answers will vary.
f′(0) does not exist; f′′(x)<0 if x<0; f′′(x)>0 if x>0 and f(0)=1.
![]() In Problems 97–100, for each function:
In Problems 97–100, for each function:
- (a) Determine the intervals on which f is concave up and on which it is concave down.
- (b) Find any points of inflection.
- (c) Graph f and describe the behavior of f at each inflection point.
f(x)=e−(x−2)2
- (a) Concave up on (−∞,2−√22)∪(2+√22,∞), concave down on (2−√22,2+√22)
- (b) (2−√22,1√e), (2+√22,1√e)
- (c)
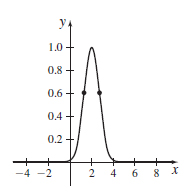
f(x)=x2√5−x
f(x)=2−x2x2−2x+1
- (a) Concave up on (−∞,0.135)∪(0.721,5.144), concave down on (0.135,0.721)∪(5.144,∞)
- (b) (0.135,2.433), (0.721,2.139), (5.144,−0.072)
- (c)
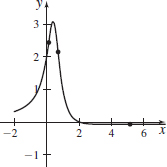
f(x)=3xx2+3x+5
Critical Number Show that 0 is the only critical number of f(x)=3√x and that f has no local extrema.
See Student Solutions Manual.
Critical Number Show that 0 is the only critical number of f(x)=3√x2 and that f has a local minimum at 0.
Inflection Point For the function f(x)=ax3+bx2, find a and b so that the point (1,6) is an inflection point of f.
a=−3, b=9
Inflection Point For the cubic polynomial function f(x)=ax3+bx2+cx+d, find a, b, c, and d so that 0 is a critical number, f(0)=4, and the point (1,−2) is an inflection point of f.
Public Health In a town of 50,000 people, the number of people at time t who have influenza is N(t)=10,0001+9999e−t, where t is measured in days. Note that the flu is spread by the one person who has it at t=0.
- (a) Find the rate of change of the number of infected people.
- (b) When is N′(t) increasing? When is it decreasing?
- (c) When is the rate of change of the number of infected people a maximum?
- (d) Find any inflection points of N(t).
- (e) Interpret the result found in (d).
- (a) N′(t)=99,990,000e−t(1+9999e−t)2
- (b) N′(t) is increasing on the interval (0,ln9999) and decreasing on the interval (ln9999,∞).
- (c) ln9999
- (d) (ln9999,5000)
- (e) Answers will vary.
Business The profit P (in millions of dollars) generated by introducing a new technology is expected to follow the logistic function P(t)=3001+50e−0.2t, where t is the number of years after its release.
- (a) When is annual profit increasing? When is it decreasing?
- (b) Find the rate of change in profit.
- (c) When is the rate of change in profit P′ increasing? When is it decreasing?
- (d) When is the rate of change in profit a maximum?
- (e) Find any inflection points of P(t).
- (f) Interpret the result found in (e).
Population Model The following data represent the population of the United States:
Year Population Year Population 1900 76,212,168 1960 179,323,175 1910 92,228,486 1970 203,302,031 1920 106,021,537 1980 226,542,203 1930 123,202,624 1990 248,709,873 1940 132,164,569 2000 281,421,906 1950 151,325,798 2010 308,745,538 An ecologist finds the data fit the logistic function P(t)=762,176,717.81+8.7427e−0.0162t.
- (a)
 Draw a scatterplot of the data using the years since 1900 as the independent variable and population as the dependent variable.
Draw a scatterplot of the data using the years since 1900 as the independent variable and population as the dependent variable. - (b)
 Verify that P is the logistic function of best fit.
Verify that P is the logistic function of best fit. - (c) Find the rate of change in population.
- (d) When is P′(t) increasing? When is it decreasing?
- (e) When is the rate of change in population a maximum?
- (f) Find any inflection points of P(t).
- (g) Interpret the result found in (f).
Source: U.S. Census Bureau.
- (a)
- (a)

- (b) Answers will vary.
- (c) P′(t)=107952118.9e−0.162t(1+8.743e−0.162t)2
- (d) P′(t) is increasing on the interval (0,133.843) and decreasing on the interval (133.843,∞).
- (e) The rate of change in population is maximum when t = 133.843.
- (f) (133.843,381088358.9)
- (g) Answers will vary.
Biology The amount of yeast biomass in a culture after t hours is given in the table below.
Time in hours Yeast Biomass Time in hours Yeast Biomass Time in hours Yeast Biomass 0 9.6 7 257.3 13 629.4 1 18.3 8 350.7 14 640.8 2 29.0 9 441.0 15 651.1 3 47.2 10 513.3 16 655.9 4 71.1 11 559.7 17 659.6 5 119.1 12 594.8 18 661.8 6 174.6 Source: Tor Carlson, Uber Geschwindigkeit und Grosse der Hefevermehrung in Wurrze, Biochemische Zeitschrift, Bd. 57, 1913, pp. 313–334.
The logistic function y=663.01+71.6e−0.5470t, where t is time, models the data.
- (a)
 Draw a scatterplot of the data using time t as the independent variable.
Draw a scatterplot of the data using time t as the independent variable. - (b)
 Verify that y is the logistic function of best fit.
Verify that y is the logistic function of best fit. - (c) Find the rate of change in biomass.
- (d) When is y′(t) increasing? When is it decreasing?
- (e) When is the rate of change in the biomass a maximum?
- (f) Find any inflection points of y(t).
- (g) Interpret the result found in (f).
- (a)
297
U.S. Budget The United States budget documents the amount of money (revenue) the federal government takes in (through taxes, for example) and the amount (expenses) it pays out (for social programs, defense, etc.). When revenue exceeds expenses, we say there is a budget surplus, and when expenses exceed revenue, there is a budget deficit. The function B=B(t)=−12.8t3+163.4t2−614.0t+390.6
where 0≤t≤9 approximates revenue minus expenses for the years 2000 to 2009, with t=0 representing the year 2000 and B in billions of dollars.
- (a) Find all the local extrema of B. (Round the answers to two decimal places.)
- (b) Do the local extreme values represent a budget surplus or a budget deficit?
- (c) Find the intervals on which B is concave up or concave down. Identify any inflection points of B.
- (d) What does the concavity on either side of the inflection point(s) indicate about the rate of change of the budget? Is it increasing at an increasing rate? Increasing at a decreasing rate?
- (e)
 Graph the function B. Given that the total amount the government paid out in 2011 was 3.6 trillion dollars, does B seem to be an accurate predictor for the budget for the years 2010 and beyond?
Graph the function B. Given that the total amount the government paid out in 2011 was 3.6 trillion dollars, does B seem to be an accurate predictor for the budget for the years 2010 and beyond?
- (a) Local minimum B(2.80)≈−328.53 billion dollars, local maximum B(5.71)≈−170.80 billion dollars.
- (b) Both represent a budget deficit.
- (c) Concave up on (0,4.26), concave down on (4.26,9), (4.26,−249.27) is a point of inflection.
- (d) To the left of the inflection point, the budget is increasing at an increasing rate. To the immediate right of the inflection point, the budget is increasing at a decreasing rate.
- (e)

Answers will vary.
If f(x)=ax3+bx2+cx+d, a≠0, how does the quantity b2−3ac determine the number of potential local extrema?
If f(x)=ax3+bx2+cx+d, a≠0, find a, b, c, and d so that f has a local minimum at 0, a local maximum at 4, and the graph contains the points (0,5) and (4,33).
a=−78, b=214, c=0, and d=5
Find the local minimum of the function f(x)=2x+81−x,0<x<1.
Find the local extrema and the inflection points of y=√3sinx+cosx, 0≤x≤2π.
Local maximum 2 at x=π3, local minimum −2 at x=4π3. Inflection points (5π6,0), (11π6,0)
If x>0 and n>1, can the expression xn−n(x−1)−1 ever be negative?
Why must the First Derivative Test be used to find the local extreme values of the function f(x)=x2/3?
f″ does not exist at the critical number x = 0.
Put It Together Which of the following is true of the function f(x)=x^{2}+e^{-2x}
- (a) f is increasing, {\bf (b)} f is decreasing, {\bf (c)} f is discontinuous at 0
- (b) f is concave up, {\bf (e)} f is concave down
Put It Together If a function f is continuous for all x and if f has a local maximum at (-1,4) and a local minimum at (3,-2), which of the following statements must be true?
- (a) The graph of f has an inflection point somewhere between x=-1 and x=3.
- (b) f^\prime (-1)=0.
- (c) The graph of f has a horizontal asymptote.
- (d) The graph of f has a horizontal tangent line at x=3.
- (e) The graph of f intersects both axes.
(e)
Vertex of a Parabola If f(x)\,=\,ax^{2}\,+\,bx\,+\,c, a\,\neq \,0, prove that f has a local maximum at -\dfrac{b}{2a} if a<0 and has a local minimum at -\dfrac{b}{2a} if a\,>\,0.
Show that \sin x\leq x, \ 0\leq x\leq 2\pi. (Hint: Let f(x)=x- \sin x.)
See Student Solutions Manual.
Show that 1-\dfrac{x^{2}}{2}\leq \cos x, \ 0\leq x\leq 2\pi. (Hint: Use the result of Problem 119.)
Show that 2 \sqrt{x}>3-\dfrac{1}{x}, for x>1.
See Student Solutions Manual.
Use calculus to show that x^{2}-8x+21>0 for all x.
Use calculus to show that 3x^{4}-4x^{3}-12x^{2}+40>0 for all x.
See Student Solutions Manual.
Show that the function f(x)=ax^{2}+bx+c, a\neq 0, has no inflection points. For what values of a is f concave up? For what values of a is f concave down?
Show that every polynomial function of degree 3 f(x)=ax^{3}+bx^{2}+cx+ d has exactly one inflection point.
See Student Solutions Manual.
Prove that a polynomial of degree n\geq 3 has at most ( n-1) critical numbers and at most ( n-2) inflection points.
Show that the function f(x)=(x-a)^{n}, a a constant, has exactly one inflection point if n\geq 3 is an odd integer.
See Student Solutions Manual.
Show that the function f(x)=(x-a)^{n}, a a constant, has no inflection point if n\geq 2 is an even integer.
Show that the function f(x)=\dfrac{ax+b}{ax+d} has no critical points and no inflection points.
See Student Solutions Manual.
First Derivative Test Proof Let f be a function that is continuous on some interval I. Suppose c is a critical number of f and (a,b) is some open interval in I containing c. Prove that if f^\prime (x)<0 for a<x<c and f^\prime (x) >0 for c<x<b, then f( c) is a local minimum value.
First Derivative Test Proof Let f be a function that is continuous on some interval I. Suppose c is a critical number of f and (a,b) is some open interval in I containing c. Prove that if f^\prime (x) has the same sign on both sides of c, then f( c) is neither a local maximum value nor a local minimum value.
See Student Solutions Manual.
Test of Concavity Proof Let f denote a function that is continuous on a closed interval [a,b]. Suppose f^\prime and f^{\prime \prime} exist on the open interval (a,b). Prove that if f^{\prime \prime}(x)<0 on the interval (a,b), then f is concave down on ( a,b).
Second Derivative Test Proof Let f be a function for which f^\prime and f^{\prime \prime} exist on an open interval (a,b). Suppose c lies in ( a,b) and is a critical number of f. Prove that if f^{\prime \prime} ( c) >0, then f( c) is alocal minimum value.
See Student Solutions Manual.
Challenge Problems
Find the inflection point of y=\left( x+1\right) \tan ^{-1}x.
Bernoulli’s Inequality Prove Bernoulli’s inequality: ( 1+x) ^{n}>1+nx for x>-1, x\neq 0, and n>1. (Hint: Let f(x)=(1+x)^{n}-(1+nx).)
See Student Solutions Manual.