5.4 Assess Your Understanding
Concepts and Vocabulary
Question
True or False \(\int_{2}^{3} (x^{2}+x)\, dx=\int_{2}^{3} x^{2}dx+\int_{2}^{3} x\, dx\)
Question
True or False \(\int_{0}^{3}5e^{x^{2}}dx=\int_{0}^{3}5\, dx\cdot \int_{0}^{3}e^{x^{2}}dx\)
Question
True or False \(\int_{0}^{5} (x^{3}+1) dx=\int_{0}^{-3}( x^{3}+1)dx\) \(+\int_{-3}^{5} (x^{3}+1) dx\)
Question
If \(f\) is continuous on an interval containing the numbers \(a,\) \(b\), and \(c,\) and if \(\int_{a}^{c}f(x)\, dx=3\) and \(\int_{c}^{b}f(x)\, dx=-5,\) then \(\int_{a}^{b}f(x) dx=\)_________.
Question
If a function \(f\) is continuous on the closed interval \([a,b],\) then \(\bar{y}=\dfrac{1}{b-a}\int_{a}^{b}f(x)\,dx\) is the ______ ______ of \(f\) over \([a,b].\)
375
Question
True or False If a function \(f\) is continuous on a closed interval \([a,b]\) and if \(m\) and \(M\) denote the absolute minimum value and the absolute maximum value, respectively, of \(f\) on \([a,b]\), then \[ m\leq \int_{a}^{b}f(x)\,dx\leq M. \]
Skill Building
In Problems 7–12, find each definite integral given that \({\int_{1}^{3}{f(x)\,dx}}=5\), \({\int_{1}^{3}}\,g{(x)\,dx}={-}2\), \({\int_{3}^{5}{f(x)\,dx}}=2\), \({\int_{3}^{5}{g(x)\,dx}}=1.\)
Question
\(\int_{1}^{3} [f(x)-g(x)]\,dx \)
Question
\(\int_{1}^{3} [f(x)+g(x)]\,dx \)
Question
\(\int_{1}^{3} [5f(x)-3g(x)]\,dx \)
Question
\(\int_{1}^{3}[3f(x)+4g(x)]\,dx\)
Question
\(\int_{1}^{5}[2f(x)-3g(x)]\,dx \)
Question
\(\int_{1}^{5}[f(x)-g(x)]\,dx\)
In Problems 13–32, find each definite integral using the Fundamental Theorem of Calculus.
Question
\(\int_{0}^{1}{({t^{2}-t^{3/2}})}\,dt \)
Question
\(\int_{-2}^{0}{({x+x^{2}})\, dx}\)
Question
\(\int_{\pi /2}^{\pi}{4\sin x\, dx}\)
Question
\(\int_{0}^{1}{3x^{2}} dx \)
Question
\(\int_{1}^{e}-\dfrac{3}{x}\,dx\)
Question
\(\int_{e}^{8}\dfrac{1}{2x}dx\)
Question
\(\int_{-\pi /4}^{\pi /4}(1+2\sec x\,\tan x)\,dx \)
Question
\(\int_{0}^{\pi /4}(1+\sec ^{2}x) \,dx\)
Question
\(\int_{1}^{4}(\sqrt{x}-4x)\,dx \)
Question
\(\int_{0}^{1}({\sqrt[5]{{t^{2}}}+1})\,dt \)
Question
\(\int_{-2}^{3}[({x-1})\,(x+3)] \,{dx} \)
Question
\(\int_{0}^{1}({z^{2}+1})^{2}dz\)
Question
\(\int_{1}^{2}{\dfrac{x^{2}-12}{x^{4}}}\,dx \)
Question
\(\int_{1}^{e}\dfrac{5s^{2}+s}{s^{2}}ds\)
Question
\(\int_{1}^{4}\dfrac{x+1}{\sqrt{x}} dx\)
Question
\(\int_{1}^{9}{\dfrac{\sqrt{x}+1}{x^{2}}} dx \)
Question
\(\int_{1}^{2}{\dfrac{2{x^{4}+1}}{x^{4}}} dx\)
Question
\(\int_{1}^{3}{\dfrac{2-x^{2}}{x^{4}}} dx \)
Question
\(\int_{0}^{1/2}\left( 5+\dfrac{1}{\sqrt{1-x^{2}}} \right) dx\)
Question
\(\int_{0}^{1}\left(1+\dfrac{5}{1+x^{2}}\right) dx\)
In Problems 33–38, use properties of integrals and the Fundamental Theorem of Calculus to find each integral.
Question
\(\int_{-2}^{1}\,f(x)\,dx\), where \(f(x)={{\left\{ \begin{array}{c@{ }c@{ }c} 1 & \hbox{if} & x\lt0 \\ x^{2}+1 & \hbox{if} & x\geq 0 \end{array} \right.}}\)
Question
\({{\int_{-1}^{-2}\,}}f(x)\,dx\), where \(f(x)={ {\left\{ \begin{array}{c@{ }c@{ }c} x+1 & \hbox{if} & x\lt0 \\ x^{2}+1 & \hbox{if} & x\geq 0 \end{array} \right.}}\)
Question
\(\int_{-2}^{2}\,f(x)\,dx\), where \(f(x)={{\left\{ \begin{array}{c@{ }c@{ }c} 3x & \hbox{if} & -2\leq x\lt0 \\ 2x^{2} & \hbox{if} & 0\leq x\leq 2 \end{array} \right. }}\)
Question
\(\int_{0}^{4}h(x)\,dx\), where \(h(x)={{\left\{ \begin{array}{c@{ }c@{ }c} x-2 & \hbox{if} & 0\leq x\leq 2 \\ 2-x & \hbox{if} & 2\lt x\leq 4 \end{array} \right. }}\)
Question
\(\int_{-2}^{1}H(x)\,dx\), where \(H(x)={{\left\{ \begin{array}{c@{ }c@{ }c} 1+x^{2} & \hbox{if} & -2\leq x\lt0 \\ 1+3x & \hbox{if} & 0\leq x\leq 1 \end{array} \right. }}\)
Question
\(\int_{-\pi /2}^{\pi /2}f(x)\,dx\), where \(f(x)=\left\{ \begin{array}{@{}l@{ }l@{ }l} {x^{2}+x} & \hbox{{if}} & {\ -{\dfrac{{\pi }}{{2}}}\leq x\leq 0} \\ {\sin x} & \hbox{{if}} & {0\lt x\lt{\dfrac{{\pi }}{{4}}}} \\ \dfrac{\sqrt{2}}{2} & \hbox{{if}} & {{\dfrac{{\pi }}{{4}}}\leq x\leq {\dfrac{{ \pi }}{{2}}}} \end{array} \right.\)
In Problems 39–42, the domain of \(f\) is a closed interval \([a,b]\). Find \(\int_{a}^{b}f(x) \,dx\).
Question
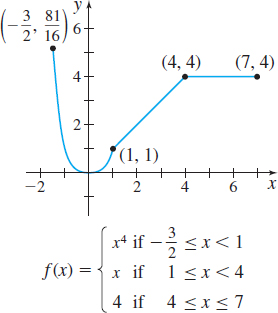
Question
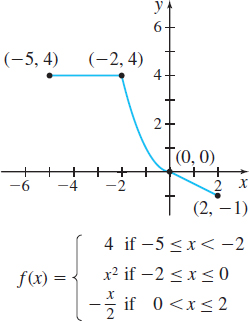
Question
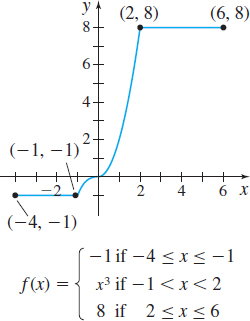
Question
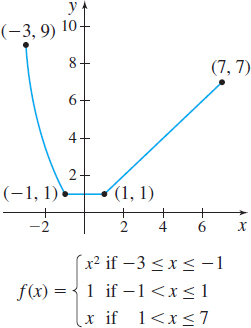
In Problems 43–46, use properties of definite integrals to verify each statement. Assume that all integrals involved exist.
Question
\(\int_{3}^{11}{f(x)\,dx-{\int_{7}^{11}{f(x)\,dx}}}=\int_{3}^{7}{f(x)\,dx}{}\)
Question
\(\int_{-2}^{6}f(x)\,dx-{\int_{3}^{6}{f(x)\,dx}=\int_{-2}^{3}{f(x)\,dx}}\)
Question
\(\int_{0}^{4}{f(x)\,dx-{\int_{6}^{4}}}f(x)\,dx=\int_{0}^{6}f(x)\,dx \)
Question
\(\int_{-1}^{3}f(x)\,dx-{\int_{5}^{3}{f(x)\,dx=\int_{-1}^{5}{f(x)\,dx}}}\)
376
In Problems 47–54, use the Bounds on an Integral Theorem to obtain a lower estimate and an upper estimate for each integral.
Question
\(\int_{1}^{3}{({5x+1})\,dx} \)
Question
\(\int_{0}^{1}{({1-x})\,dx} \)
Question
\(\int_{\pi /4}^{\pi /2}{\sin x\,dx} \)
Question
\(\int_{\pi /6}^{\pi /3}{\cos x\,dx}\)
Question
\(\int_{0}^{1}{\sqrt{1+x^{2}}\,dx }\)
Question
\(\int_{-1}^{1}{\sqrt{1+x^{4}}\,dx}\)
Question
\(\int_{0}^{1}e^{x}dx\)
Question
\(\int_{1}^{10}\dfrac{1}{x}dx \)
In Problems 55–60, for each integral find the number(s) \(u\) guaranteed by the Mean Value Theorem for Integrals.
Question
\(\int_{0}^{3} (2{x^{2} + 1}) dx\)
Question
\(\int_{0}^{2} (2-x^{3}) \,dx \)
Question
\(\int_{0}^{4}x^{2}\,dx \)
Question
\(\int_{0}^{4}(-x)\,dx \)
Question
\(\int_{0}^{2\pi }\cos x\,dx \)
Question
\(\int_{-\pi/4}^{\pi /4}\sec x\tan x dx\)
In Problems 61–70, find the average value of each function \(f\) over the given interval.
Question
\(f(x) =e^{x}\) over \([0,1]\)
Question
\(f(x) =\dfrac{1}{x}\) over \([1,e] \)
Question
\(f(x) =x^{2/3}\) over \([-1,1] \)
Question
\(f(x) =\sqrt{x}\) over \([0,4] \)
Question
\(f(x) =\sin x\) over \(\left[0,\dfrac{{\pi }}{2}\right] \)
Question
\(f(x) =\cos x\) over \(\left[ 0,\dfrac{{\pi }}{2} \right]\)
Question
\(f(x) =1-x^{2}\) over \([-1,1] \)
Question
\(f(x) =16-x^{2}\) over \([-4,\,4] \)
Question
\(f(x) =e^{x}-{\sin x}\) over \(\left[0,\dfrac{\pi}{2}\right] \)
Question
\(f(x) =x+\cos x\) over \(\left[0,\dfrac{{\pi }}{2}\right] \)
In Problems 71–74, find:
- The area under the graph of the function over the indicated interval.
- The average value of each function over the indicated interval.
- Interpret the results geometrically.
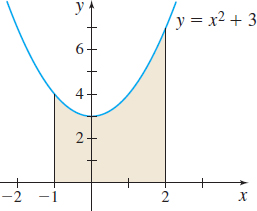
Question
\([-1, 2]\)
Question
\([-2, 1]\)
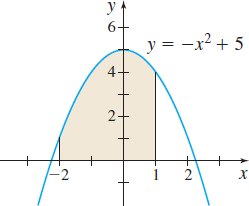
Question
\([-1, 2]\)
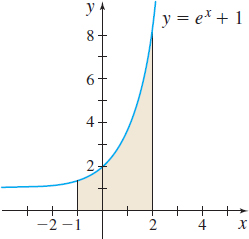
Question
\([0, \frac{3\pi}{4}]\)
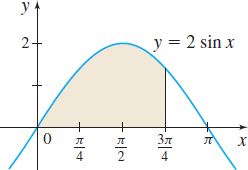
Applications and Extensions
In Problems 75–78, find each definite integral using the Fundamental Theorem of Calculus and properties of definite integrals.
Question
\(\int_{-2}^{3}{({x+{|x|}})\,dx}\)
Question
\(\int_{0}^{3}{{|x-1|}\,dx} \)
Question
\(\int_{0}^{2}{{|3x-1|}\,dx} \)
Question
\(\int_{0}^{2}\vert {2-x} \vert dx\)
Question
Average Temperature A rod \(3\) meters long is heated to \(25x^{\circ}{\rm C}\), where \(x\) is the distance in meters from one end of the rod. Find the average temperature of the rod.
Question
Average Daily Rainfall The rainfall per day, \(x\) days after the beginning of the year, is modeled by the function \(r(x)=0.00002(6511+366x-x^{2}) \), measured in centimeters. Find the average daily rainfall for the first \(180\) days of the year.
Question
Structural Engineering A structural engineer designing a member of a structure must consider the forces that will act on that member. Most often, natural forces like snow, wind, or rain distribute force over the entire member. For practical purposes, however, an engineer determines the distributed force as a single resultant force acting at one point on the member. If the distributed force is given by the function \(W=W(x)\), in newtons per meter (N/m), then the magnitude \(F_{R}\) of the resultant force is \[ F_{R}=\int_{a}^{b}W(x)\, dx \]
The position \(\bar{x}\) of the resultant force measured in meters from the origin is given by \[ \overline{x}=\dfrac{\int_{a}^{b}xW(x)\, dx}{\int_{a}^{b}W(x)\, dx} \]
If the distributed force is \(W(x) =0.75x^{3},\) \(0\leq x\leq 5,\) find:
- The magnitude of the resultant force.
- The position from the origin of the resultant force.
source: Problem contributed by the students at Trine University, Avalon, IN.
Question
Chemistry: Enthalpy In chemistry, enthalpy is a measure of the total energy of a system. For a nonreactive process with no phase change, the change in enthalpy \(\Delta H\) is given by \(\Delta H=\) \(\int_{T_{1}}^{T_{2}}C_{p}\, dT,\) where \(C_{p}\) is the specific heat of the system in question. The specific heat per mol of the chemical benzene is \[ C_{p} =0.126+(2.34\times 10^{-6}) T, \]
377
where \(C_{p}\) is in \(kJ/\left(mol {}^{\circ}{\rm C} \right)\), and \(T\) is in degrees Celsius.
- What are the units of the change in enthalpy \(\Delta H?\)
- What is the change in enthalpy \(\Delta H\) associated with increasing the temperature of 1.0 mol of benzene from \(20{}^{\circ}{\rm C}\) to \(40{}^{\circ}{\rm C}\)?
- What is the change in enthalpy \(\Delta H\) associated with increasing the temperature of 1.0 mol of benzene from \(20{}^{\circ}{\rm C}\) to \(60{}^{\circ}{\rm C}\)?
- Does the enthalpy of benzene increase, decrease, or remain constant as the temperature increases?
source: Problem contributed by the students at Trine University, Avalon, IN.
Question
Average Mass Density The mass density of a metal bar of length \(3\) meters is given by \(\rho (x) = 1000 + x - \sqrt{x}\) kilograms per cubic meter, where \(x\) is the distance in meters from one end of the bar. What is the average mass density over the length of the entire bar?
Question
Average Velocity The acceleration at time \(t\) of an object in rectilinear motion is given by \(a(t) =4\pi \cos t\). If the object's velocity is \(0\) at \(t = 0\), what is the average velocity of the object over the interval \(0\,\leq \,t\,\leq \,\pi \)?
Question
Average Area What is the average area of all circles whose radii are between 1 and 3 m?
Question
Area
- Use properties of integrals and the Fundamental Theorem of Calculus to find the area under the graph of \(y=3 - |x|\) from \(-3\) to \(3\).
- Check your answer by using elementary geometry.
Question
Area
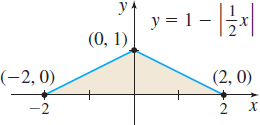
- Use properties of integrals and the Fundamental Theorem of Calculus to find the area under the graph of \(y=1-\left\vert \dfrac{1}{2}x\right\vert \) from \(-2\) to \(2.\)
- Check your answer by using elementary geometry. See the figure.
Question
Area Let \(A\) be the area in the first quadrant that is enclosed by the graphs of \(y=3x^{2},\) \(y=\dfrac{3}{x},\) the \(x\)-axis, and the line \(x=k\), where \(k>1\), as shown in the figure.
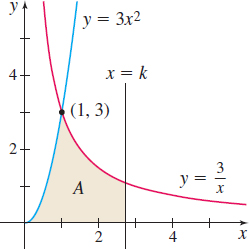
- Find the area \(A\) as a function of \(k\).
- When the area is \(7\), what is \(k\)?
- If the area \(A\) is increasing at the constant rate of \(5\) square units per second, at what rate is \(k\) increasing when \(k=15\)?
Question
Rectilinear Motion A car starting from rest accelerates at the rate of \(3\) m./s\(^{2}\). Find its average speed over the first 8 seconds.
Question
Rectilinear Motion A car moving at a constant velocity of 80 miles per hour begins to decelerate at the rate of 10 mi/h\(^{2}\). Find its average speed over the next 10 minutes.
Question
Average Slope
- Use the definition of average value of a function to find the average slope of the graph of \(y=f(x)\), where \(a\leq x\leq b\). (Assume that \(f^\prime \) is continuous.)
- Give a geometric interpretation.
Question
What theorem guarantees that the average slope found in Problem 91 is equal to \(f^{\prime }(u)\) for some \(u\) in \([a,b]?\) What different theorem guarantees the same thing? (Do you see the connection between these theorems?)
Question
Prove that if a function \(f\) is continuous on a closed interval \([a,b]\) and if \(k\) is a constant, then \(\int_{a}^{b}kf(x)\,dx=k \int_{a}^{b}f(x)\,dx\).
Question
Prove that if the functions \(f_{{1}}\), \(f_{{2}} , \ldots ,f_{n}\) are continuous on a closed interval \([a,b]\)and if \(k_{{1}}\), \(k_{{2}}, \ldots , k_{n}\) are constants, then \[ \begin{eqnarray*} &&\int_{a}^{b}[k_{{1}}f_{{1}}(x)+k_{{2}}f_{{2}}(x)+\cdots +k_{n}f_{n}(x)]\,dx \\ &&\enspace =k_{{1}}\int_{a}^{b}f_{{1}}(x)\,dx+k_{{2}}\int_{a}^{b}f_{{2}}(x)\,dx+\cdots + k_{n}\int_{a}^{b}f_{n}(x)\,dx \end{eqnarray*} \]
Question
Area The area under the graph of \(y=\cos x\) from \(-\dfrac{\pi }{2}\) to \(\dfrac{\pi }{2}\) is separated into two parts by the line \(x=k\), \(\dfrac{-\pi}{2}\lt k \lt \dfrac{\pi}{2}\), as shown in the figure. If the area under the graph of \(y\) from \(-\dfrac{\pi }{2}\) to \(k\) is three times the area under the graph of \(y\) from \(k\) to \(\dfrac{\pi }{2},\) find \(k.\)
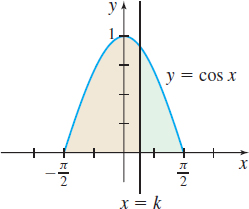
Question
Displacement of a Damped Spring The displacement \(x\) in meters of a damped spring from its equilibrium position at time \(t\) seconds is given by \[ x(t) =\dfrac{\sqrt{15}}{10}e^{-t}\sin \big(\sqrt{15}t\big) + \dfrac{3}{2}e^{-t}\cos \big(\sqrt{15}t\big) \]
- What is the displacement of the spring at \(t=0?\)
 Graph the displacement for the first \(2\) seconds of the springs' motion.
Graph the displacement for the first \(2\) seconds of the springs' motion. Find the average displacement of the spring for the first 2 seconds of its motion.
Find the average displacement of the spring for the first 2 seconds of its motion.
Question
![]() Area Let \[ f(x) =\vert x^{4}+3.44x^{3}-0.5041x^{2}-5.0882x +\,1.1523 \vert \]
Area Let \[ f(x) =\vert x^{4}+3.44x^{3}-0.5041x^{2}-5.0882x +\,1.1523 \vert \]
be defined on the interval \([-3,1] \). Find the area under the graph of \(f.\)
Question
If \(f\) is continuous on \([a,b]\), show that the functions defined by \[ F(x)= \int_{c}^{x}{f(t)\,dt} \qquad G(x)= \int_{d}^{x}{f(t)\,dt} \]
378
for any choice of \(c\) and \(d\) in \((a,b)\) always differ by a constant. Also show that \[ F(x)-G(x)={\int_{c}^{d}{f(t)\,dt}} \]
Question
Put It Together Suppose \(a\lt c\lt b\) and the function \(f\) is continuous on \([a,b]\) and differentiable on \((a,b)\). Which of the following is not necessarily true?
- \(\int_{a}^{b}f(x)\,dx= \int_{a}^{c}{f(x)\,dx}+\int_{c}^{b}f(x)\,dx\).
- There is a number \(d\) in \((a,b)\) for which \[ f^\prime (d)= \dfrac{f(b)-f(a)}{b-a} \]
- \(\int_{a}^{b}{f(x)\,dx\geq 0}\).
- \(\lim\limits_{x\rightarrow c}\,f(x)=f(c)\).
- If \(k\) is a real number, then \(\int_{a}^{b}kf(x)\,dx=k \int_{a}^{b}f(x)\,dx.\)
Question
Minimizing Area Find \(b>0\) so that the area enclosed in the first quadrant by the graph of \(y=1+b-bx^2\) and the coordinate axes is a minimum.
Question
Area Find the area enclosed by the graph of \(\sqrt{x}+\sqrt{y}=1\) and the coordinate axes.
Challenge Problems
Question
Average Speed For a freely falling object starting from rest, \(v_{0}=0,\) find:
- The average speed \(\overline{v }_{t}\) with respect to the time \(t\) in seconds over the closed interval \([0,5].\)
- The average speed \(\overline{v }_{s}\) with respect to the distance \(s\) of the object from its position at \(t=0\) over the closed interval \([0,s_{1}] \), where \(s_{1}\) is the distance the object falls from \(t=0\) to \(t=5\) seconds.
(Hint: The derivation of the formulas for freely falling objects is given in Section 4.8, pp. 334-337.)
Question
Average Speed If an object falls from rest for 3 s, find:
- Its average speed with respect to time.
- Its average speed with respect to the distance it travels in 3 seconds.
Question
Free Fall For a freely falling object starting from rest, \(v_{0}=0\), find:
- The average velocity \(\overline{v }_{t}\) with respect to the time \(t\) over the closed interval \([0,t_{1}].\)
- The average velocity \(\overline{v }_{s}\) with respect to the distance \(s\) of the object from its position at \(t=0\) over the closed interval \([0,s_{1}]\), where \(s_{1}\) is the distance the object falls in time \(t_{1}\). Assume \(s(0) =0.\)
Question
Put It Together
- What is the domain of \(f(x) =2 |x - 1| x^{2}\)?
- What is the range of \(f\)?
- For what values of \(x\) is \(f\) continuous?
- For what values of \(x\) is the derivative of \(f\) continuous?
- Find \(\int_{0}^{1}{f(x)\,dx.}\)
Question
Probability A function \(f\) that is continuous on the closed interval \([a,b],\) and for which (i) \(f(x)\geq 0\) for numbers \(x\) in \([a,b]\) and 0 elsewhere and (ii) \(\int_{a}^{b} f (x)\,dx=1,\) is called a probability density function. If \(a\leq c\lt d\leq b\), the probability of obtaining a value between \(c\) and \(d\) is defined as \(\int_{c}^{d}f(x)\,dx\).
- Find a constant \(k\) so that \(f(x)=kx\) is a probability density function on \([0,2]\).
- Find the probability of obtaining a value between \(1\) and \(1.5\).
Question
Cumulative Probability Distribution Refer to Problem 106. If \(f\) is a probability density function the cumulative distribution function \(F\) for \(f\) is defined as \[ F(x)=\int_{a}^{x}f(t)\,dt \qquad a\leq x\leq b \]
Find the cumulative distribution function \(F\) for the probability density function \(f(x) =kx\) of Problem 106(a).
Question
For the cumulative distribution function \(F(x)=x-1\), on the interval \([1,2]\):
- Find the probability density function \(f\) corresponding to \(F\).
- Find the probability of obtaining a value between \(1.5\) and \(1.7\).
Question
Let \(f(x)=x^{3}-6x^{2}+11x-6\). Find \(\int_{1}^{3}\vert f(x)\vert dx.\)
Question
Show that for \(x>1,\) \(\ln x\lt2 (\sqrt{x}-1).\)
(Hint: Use the result given on Problem 114.)
Question
Prove that the average value of a line segment \(y=m (x-x_{1} ) +y_{1}\) on the interval \([x_{1},x_{2}]\) equals the \(y\)-coordinate of the midpoint of the line segment from \(x_{1}\) to \(x_{2}.\)
Question
Prove that if a function \(f\) is continuous on a closed interval \([a,b]\) and if \(f(x)\geq 0\) on \([a,b]\), then \(\int_{a}^{b}f(x)\,dx \geq 0\).
Question
- Prove that if \(f\) is continuous on a closed interval \([a,b]\) and \({\int_{a}^{b}{f(x)\,dx=0}}\), there is at least one number \(c\) in \([a,b]\) for which \(f(c) = 0\).
- Give a counterexample to the statement above if \(f\) is not required to be continuous.
Question
Prove that if functions \(f\) and \(g\) are continuous on a closed interval \([a,b]\) and if \(f(x)\geq \,g(x)\) on \([a,b]\), then \[ \int_{a}^{b}f(x)\,dx\geq \int_{a}^{b}g(x)\,dx. \]
Question
Prove that if \(f\) is continuous on \([a,b]\), then \[ \left\vert \int_{a}^{b} f(x)\,dx\right\vert \leq \int_{a}^{b}\vert {f(x)}\vert\, dx. \]
Give a geometric interpretation of the inequality.
