Question

True or False If a function \(f\) has a derivative that is continuous on an interval containing \(a\) and \(b\), the length \(s\) of the graph of \(y=f(x)\) from \(x=a\) to \(x=b\) is given by the formula \(s=\int^b_a \sqrt{1+[f(x)]^2}~{\it dx}\).

Question

True or False If the derivative of a function \(y=\) \(f(x)\) is not continuous at some number in the interval \([a,b]\), its arc length from \(x=a\) to \(x=b\) can sometimes be found by partitioning the \(y\)-axis.

Question

\(y=3x-1\), from \((1,2)\) to \((3,8)\)

Question

\(y=-4x+1\), from \((-1,5)\) to \((1,-3)\)

Question

\(2x-3y+4=0\), from \((1,2)\) to \((4,4)\)

Question

\(3x+4y-12=0\), from \((0,3)\) to \((4,0)\)

Question

\(y=x^{2/3}+1\), from \(x=1\) to \(x=8\)

Question

\(y=x^{2/3}+6\), from \(x=1\) to \(x=8\)

Question

\(y=x^{3/2}\), from \(x=0\) to \(x=4\)

Question

\(y=x^{3/2}+4\), from \(x=1\) to \(x=4\)

Question

\(9y^{2}=4x^{3}\), from \(x=0\) to \(x=1;\) \(y\geq 0\)

Question

\(y=\dfrac{x^{3}}{6}+\dfrac{1}{2x}\), from \(x=1\) to \(x=3\)

Question

\(y=\dfrac{2}{3}(x^{2}+1)^{3/2}\), from \(x=1\) to \(x=4\)

Question

\(y=\dfrac{1}{3}(x^{2}+2)^{3/2}\), from \(x=2\) to \(x=4\)

Question

\(y=\dfrac{2}{9}\sqrt{~3}(3x^{2}+1)^{3/2}\), from \(x=-1\) to \(x=2\)

Question

\(y=(1-x^{2/3})^{3/2}\), from \(x=\dfrac{1}{8}\) to \(x=1\)

Question

\(8y=x^{4}+\dfrac{2}{x^{2}}\), from \(x=1\) to \(x=2\)

Question

\(9y^{2}=4(1+x^{2})^{3}\), from \(x=0\) to \(x=2\sqrt{2};\) \(y\geq 0\)

Question

\(y=\ln (\sin x)\), from \(x=\dfrac{\pi }{6}\) to \(x=\dfrac{\pi }{3}\)

Question

\(y=\ln (\cos x)\), from \(x=\dfrac{\pi }{6}\) to \(x=\dfrac{\pi }{3}\)

Question

\((x+1)^{3}=4y^{2}\), from \(x=-1\) to \(x=16, y\geq 0\)

Question

\(y=x^{3/2}+8\), from \(x=0\) to \(x=4\)

Question

\(y=x^{2/3}\), from \(x=0\) to \(x=1\)

Question

\(y=x^{2/3}\), from \(x=-1\) to \(x=0\)

Question

\((x+1)^{2}=4y^{3}\), from \(y=0\) to \(y=1;x\geq -1\)

Question

\(x=\dfrac{2}{3}(y-5)^{3/2}\), from \(y=5\) to \(y=6\)

Question

\(y=x^{2}\), from \(x=0\) to \(x=2\)

Question

\(x=y^{2}\), from \(y=1\) to \(y=3\)

Question

\(y=\sqrt{~25-x^{2}}\), from \(x=0\) to \(x=4\)

Question

\(x=\sqrt{~4-y^{2}}\), from \(y=0\) to \(y=1\)

Question

\(y=\sin x,\) from \(x=0\) to \(x=\dfrac{\pi }{2}\)

Question

\(x=y+\ln y\), from \(y=1\) to \(y=4\)

Question

Length of a Hypocycloid Find the total length of the hypocycloid \(x^{2/3}+y^{2/3}=a^{2/3}, a>0.\)

Question

Distance Along a Curved Path Find the distance between \((1, 1)\) and \((3, 3\sqrt{3})\) along \(y^{2}=x^{3}.\)

Question

Perimeter Find the perimeter of the region bounded by the graphs of \(y^{3}=x^{2}\) and \(y=x.\)

Question

Perimeter Find the perimeter of the region bounded by the graphs of \(y=3(x-1)^{3/2}\) and \(y=3(x-1).\)

Question

Length of a Graph Find the length of \(6xy=y^{4}+3\) from \(y=1\) to \(y=2.\)

Question

Length of a Graph Find the length of the hyperbolic function \(y=\cosh x\) from \((0,1)\) to \((2,\cosh 2).\)

Question

Length of an Graph Find the length of \(y=\ln (\csc x)\) from \(x=\dfrac{\pi }{4}\) to \(x=\dfrac{\pi }{2}.\)

Question

Length of an Elliptical Arc Set up the integral for the arc length of the ellipse \(\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1\) from \(x=0\) to \(x=\dfrac{a}{2}\) in quadrant I. This integral, which is approximated by numerical techniques (see Chapter 7), is called an elliptical integral of the second kind.

Question

Length of a Circular Arc In each case below, \(P_{1}=\left(x_{1},y_{1}\right)\) and \(P_{2}=\left( x_{2},y_{2}\right)\) are points on the circle \(x^{2}+y^{2}=1\) that do not lie on a coordinate axis. Express the length of the counterclockwise arc \(P_{1}P_{2}\) in terms of integrals of the form \[ \displaystyle \int_{u}^{v}\frac{1}{\sqrt{1-t^{2}}}~{\it dt},\qquad -1<u<v<1 \]

1. when \(P_{1}\) is in quadrant I and \(P_{2}\) is in quadrant II.
2. when \(P_{1}\) and \(P_{2}\) are both in quadrant III and \(y_{1}<y_{2}.\)
3. when \(P_{1}\) is in quadrant II and \(P_{2}\) is in quadrant IV.

Question

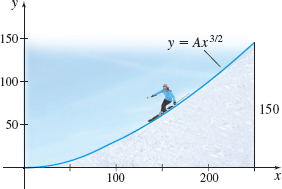
Modeling a Ski Slope A ski slope is built on a mountainside and curves upward from ground level to a height \(h\). The shape of the ski slope is modeled by the equation \(y=Ax^{3/2}\), where \(x\) is the horizontal distance from the bottom of the ski slope measured along the base of the mountain and \(y\) is the vertical height of the ski slope at the distance \(x.\)

1. Find an expression, in terms of \(A\) and \(h\), for the length of the ski slope.
2. Find \(A\) if the ski slope is \(150 \textrm{ m}\) high and has a horizontal distance of \(250\textrm{ m}\) along the base.
3. If a skier skis directly downhill from the top of the ski slope to the bottom, how far does she travel?
4. Describe a simple way to check if the distance obtained in part (c) is reasonable.

444

Question

Length of a Cable A cable hangs in the shape of a catenary between two supports at the same height \(20\) m apart. See the figure. The slope of the tangent line to the cable at the right-hand support is \(\dfrac{3}{4}\). The equation of a catenary is \(y=a\cosh \dfrac{x}{a}+b-a\), where \(a\) is a constant that depends on the linear density of the cable and the tension on the cable and \(b\) is the distance from the \(x\)-axis to the lowest point of the cable.

1. What is the height of the supports? (Hint: Let \(d\) represent the height of the supports above the lowest point \(b.)\)
2. Find the length of the cable.

Question

Equation of a Catenary A rope of length \(L\) is supported at two points, \((c,d)\) and \((-c,d)\). The middle of the rope is located at the point \((0,b)\). The shape of the rope is given by \(y=a\cosh \left( \dfrac{x}{a}\right) +b-a\). Find \(a\). [Hint: Show that \((d-b+a)^{2}-a^{2}= \dfrac{L^{2}}{4}.]\)

Question

Projectile Motion An object is launched from level ground, travels in a parabolic trajectory, and lands \(150\) m away. It reaches a maximum height of 46 m.

Question

Arc Length The arc length formula cannot be used to find the arc length from \(x=-\dfrac{\pi }{2}\) to \(x=\dfrac{\pi }{2}\) of the function \(f\) given below. Why not? \begin{equation*} f(x)=\left\{ \begin{array}{@{}l@{\qquad}ll} x\sin \dfrac{1}{x} & \hbox{ if } & x\neq 0 \\ 0 & \hbox{ if} & x=0 \end{array} \right. \end{equation*}

Question

Inscribe a regular polygon of \(2^{n}\) sides in a circle of radius 1. The figure illustrates the situation for \(n=3.\)

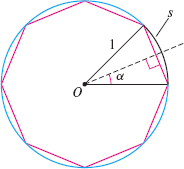
1. Show that the indicated angle \(\alpha =\dfrac{45^{\circ}}{2^{n-2}}.\)
2. Show that the formula \(s=2^{n+1} \sin \frac{45^\circ}{2^{n-2}}\) gives a good approximation to the arc length \(s\) (the circumference) of the circle.
3. Evaluate this approximation for several values of \(n\), and compare the results with the actual circumference of the circle.

Question

Using Problem 47 and a half-angle formula, show that \(2^{n+2}a_{n}\) approximates \(\pi\), where \(a_{0}=\dfrac{1}{\sqrt{2}}\) and \(a_{n+1}=\sqrt{\dfrac{1-\sqrt{1-a_{n}^{2}}}{2}}\), \(n=0,1,2,\ldots\) Evaluate \(2^{n+2}a_{n}\) for several values of \(n\) and compare your answer with \(\pi.\)

Question

Find \(y=f(x)\) if the arc length \(s\) of \(y=f(x)\) from \(0\) to \(x\) satisfies \(s=e^{x}-y\) and \(f(0)=1.\)