6.8 Assess Your UnderstandingPrinted Page 465
465
Concepts and Vocabulary
Multiple Choice The [(a) midpoint of mass, (b) mass point, (c) center of mass] of a system is the point that acts as if all the mass is concentrated at that point.
(c)
Multiple Choice If an object of mass m is located on the x-axis a distance d from the origin, then the moment of the mass about the origin is [(a) 0, (b) d, (c) md, (d) m].
(c)
True or False A homogeneous lamina is made of material that has a constant density.
True
Multiple Choice If a homogeneous lamina is symmetric about a line L, then its [(a) centroid, (b) moment of mass, (c) axis] lies on L.
(a)
True or False The centroid of a lamina R always lies within R.
False
Multiple Choice The center of mass of a homogeneous lamina R is located at the [(a) centroid, (b) midpoint, (c) equilibrium point] of R, the geometric center of the lamina.
(a)
Skill Building
In Problems 7–10, find the center of mass of each system of masses.
m1=20,m2=50 located, respectively, at 4 and 10
ˉx=587
m1=10,m2=3 located, respectively, at −2 and 3
m1=4,m2=3,m3=3,m4=5 located, respectively, at −1,2,4,3
ˉx=2915
m1=7,m2=3,m3=2,m4=4 located, respectively, at 6,−2,−4,−1
In Problems 11–14, find the moments Mx and My and the center of mass of each system of masses.
m1=4,m2=8,m3=1 located, respectively, at the points (0,2),(2,1),(4,8)
My=20, Mx=24, (ˉx,ˉy)=(2013,2413)
m1=6,m2=2,m3=10 located, respectively, at the points (−1,−1),(12,6),(−1,−2)
m1=4,m2=3,m3=3,m4=5 located, respectively, at the points (−1,2),(2,3),(4,5),(3,6)
My=29,Mx=62,(ˉx,ˉy)=(2915,6215)
m1=8,m2=6,m3=3,m4=5 located, respectively, at the points (−4,4),(0,5),(6,4),(−3,−5)
In Problems 15–22, find the centroid of each homogeneous lamina bounded by the graphs of the given equations.
y=2x+3,y=0,x=−1,x=2
(78,198)
y=3−x2,y=0,x=−1,x=3
y=x2,y=0,x=3
(94,2710)
y=x3,x=2,y=0
y=4x−x2 and the x-axis
(2,85)
y=x2+x+1,x=0,x=4, and the x-axis
y=√x,x=4,y=0
(125,34)
y=3√x,x=8,y=0
In Problems 23 and 24, use the Pappus Theorem to find the volume of the solid of revolution.
The solid torus formed by revolving the circle (x−4)2+y2=9 about the y-axis
72π2
The solid torus formed by revolving the circle x2+(y−2)2=1 about the x-axis
Applications and Extensions
Centroid In Problems 25–30, find the centroid of each homogeneous lamina. (Hint: The moments of the union of two or more nonoverlapping regions equals the sum of the moments of the individual regions.)
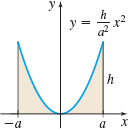
(1,4+3π4+π)
(a3,b3)
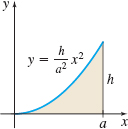
(3a4,3h10)
Center of Mass of a Baseball Bat Inspection of a baseball bat shows that it gets progressively thicker, that is, more massive, beginning at the handle and ending at the top. If the bat is aligned so that the x-axis runs through the center of the bat, the density λ, in kilograms per meter, can be modeled by λ=kx, where k is the constant of proportionality. The mass M of a bat of length L meters is ∫L0λ dx. The center of mass ¯x of the bat is ∫L0xλ dxM.
- (a) Find the mass of the bat.
- (b) Use the result of (a) to find the constant of proportionality k.
- (c) Find the center of mass of the bat.
- (d) Where is the “sweet spot” of the bat (the best place to make contact with the ball)? Explain why?
- (e) Give an explanation for the representation of the mass M by ∫L0λ dx.
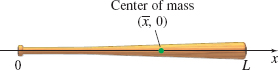
- (a) M=kL22
- (b) k=2ML2
- (c) ˉx=23L
- (d) Answers will vary.
- (e) Answers will vary.
466
The Pappus Theorem for Volume Find the volume of the solid formed by revolving the region bounded by the graphs of y=√x−1,y=0, and x=2 about the y-axis.
The Pappus Theorem for Volume Find the volume of the solid formed by revolving the triangular region bounded by the lines x=3,y=2, and x+2y=9 about the y-axis.
22π3
The Pappus Theorem for Volume Find the volume of a right circular cone of radius R and height H.
The Pappus Theorem for Volume Find the volume of the solid formed by revolving the triangular region whose vertices are at the points (1,1),(5,3), and (3,3) about the x-axis.
28π3
Centroid of a Right Triangle Find the centroid of a triangular region with vertices at (0,0), (0,4), and (3,0).
Challenge Problems
Centroid of a Triangle
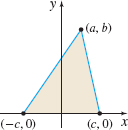
- (a) Show that the centroid of a triangular region is located at the intersection of the medians. [Hint: Place the vertices of the triangle at (a,0), (b,0), and (0,c), a<0, b>0, c>0.
- (b) Show that the centroid of a triangular region divides each median into two segments whose lengths are in the ratio 2:1.
See Student Solutions Manual.
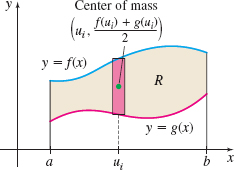
Derive formulas for finding the centroid of a lamina bounded by the graphs of y=f(x) and y=g(x) and the lines x=a and x=b, as shown in the figure below.
In Problems 39–44, use the result of Problem 38 to find the centroid of each homogeneous lamina enclosed by the graphs of the given equations.
y=x2/3 and y=x2 from x=−1 to x=1
(0,37)
y=1x, and the lines y=14, and x=1
y=−x2+2 and y=|x|
(0,3835)
y=√x and y=x2
y=4−x2 and y=x+2.
(−12,125)
y=9−x2 and y=|x|.
Laminas with Variable Density Suppose a lamina is determined by a region R enclosed by the graph of y=f(x), the x-axis, and the lines x=a and x=b, where f is continuous and nonnegative on the closed interval [a,b]. Suppose further that the density of the material at (x,y) is ρ=ρ(x), where ρ is continuous on [a,b]. Show that the center of mass (ˉx,ˉy) of R is given by ˉx=MyM=∫baρ(x)xf(x) dx∫baρ(x)f(x)dxˉy=MxM=12∫baρ(x)[f(x)]2dx∫baρ(x)f(x)dx
(Hint: Partition the interval [a,b] into n subintervals, and use an argument similar to the one used for the centroid of a homogeneous lamina. Assume that if Δx is small, then Ri is homogeneous.)
See Student Solutions Manual.
Lamina with Variable Density Use the results of Problem 45 to find the center of mass of a lamina enclosed by f(x)=12x2, the x-axis, and the lines x=1 and x=e. Suppose the density at any point (x,y) of the lamina is ρ(x)=1x3.
Lamina with Variable Density Use the results of Problem 45 to find the center of mass of the lamina enclosed by y=√x+1, and the lines x=0 and y=3, where the density of the lamina is ρ(x)=x.
(836217,8031)
Laminas with Variable Density In Problems 48–51, use the results of Problem 45 to find the center of mass of each lamina enclosed by the graph of f on the given interval and having density ρ=ρ(x).
f(x)=x;[0,3];ρ(x)=x
f(x)=3x−1;[1,4];ρ(x)=x
(22774,607148)
f(x)=2x;[0,1];ρ(x)=x+1
f(x)=x;[1,4];ρ(x)=x+1
(11338,11376)