Applications of the Integral

Printed Page 469

CHAPTER 6 PROJECTDetermining the Amount of Concrete Needed for a Cooling Tower

469

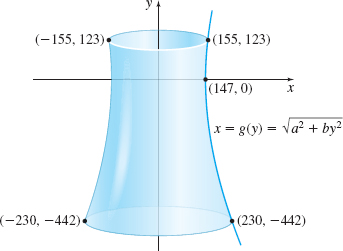
A common design for cooling towers is modeled by a branch of a hyperbola rotated about an axis. The design is used because of its strength and efficiency. Not only is the shape stronger than either a cone or cylinder, it takes less material to build. This shape also maximizes the natural upward draft of hot air without the need for fans.*

How much concrete is needed to build a cooling tower that has a base $460\textrm{ ft}$ wide that is $442\text{ft}$ below the vertex if the top of the tower is $310\text{ft}$ wide and $123\text{ft}$ above the vertex? Assume the walls are a constant $5\text{in}$ $=0.42\text{ft}$ thick. See Figure 76.

Figure 76

470

Show that the equation of the right branch of the hyperbola in Figure 76 is given by $x=g_{2}(y)=\sqrt{a^{2}+by^{2}}$

where $a=147$ and $b=0.16.$

Find the volume of the solid of revolution obtained by revolving the area enclosed by $x=g_{2}(y)$ from $y=-442$ to $y=123$ about the $y$ -axis.

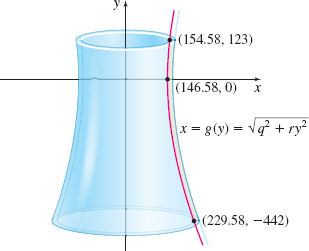
Using the fact that the walls are $0.42\text{ft}$ thick, show that the equation of the interior hyperbola is given by $x=g_{1}(y)=\sqrt{q^{2}+ry^{2}}$

where $q=146.58$ and $r=0.16$ . See Figure 77.

Figure 77

Find the volume of the solid of revolution obtained by revolving the area enclosed by $x=g_{1}(y)$ from $y=-442$ to $y=123$ about the $y$ -axis.

Now determine the volume (in cubic feet) of concrete required for the cooling tower.

Do an Internet search to find the cost of concrete. How much will the concrete used in the cooling tower cost?

Write a report for an audience that is not familiar with cooling towers summarizing the findings in Problems 1–6.

For pictures of the cooling towers and power plant, as well as a time-lapse video of the towers being built, log onto https://www.dom.com/about/stations/fossil/brayton-point-power-station.jsp

*The design of an unsupported, reinforced concrete hyperbolic cooling tower was patented in 1918 (UK patent 198,863) by Frederic von Herson and Gerard Kupeers of the Netherlands.

Source: Excerpts from The Providence Journal, Frieda Squires, May 2010.