7.5 Assess Your UnderstandingPrinted Page 506
506
Concepts and Vocabulary
Multiple Choice A rational function R(x)=p(x)q(x) is proper when the degree of p is [(a) less than, (b) equal to, (c) greater than] the degree of q.
(a)
True or False Every improper rational function can be written as the sum of a polynomial and a proper rational function.
True
True or False Sometimes the integration of a proper rational function leads to a logarithm.
True
True or False The decomposition of 7x+1(x+1)4 into partial fractions has three terms: Ax+1+B(x+1)2+C(x+1)3, where A, B, and C are real numbers.
False
Skill Building
In Problems 5–8, find each integral by first writing the integrand as the sum of a polynomial and a proper rational function.
∫x2+1x+1dx
x22−x+2ln|x+1|+C
∫x2+4x−2dx
∫x3+3x−4x−2dx
x33+x2+7x+10ln|x−2|+C
∫x3−3x2+4x+3dx
In Problems 9–14, find each integral. (Hint: Each of the denominators contains only distinct linear factors.)
∫dx(x−2)(x+1)
13ln|x−2|−13ln|x+1|+C
∫dx(x+4)(x−1)
∫xdx(x−1)(x−2)
−ln|x−1|+2ln|x−2|+C
∫3xdx(x+2)(x−4)
∫xdx(3x−2)(2x+1)
221ln|3x−2|+114ln|2x+1|+C
∫dx(2x+3)(4x−1)
In Problems 15–18, find each integral. (Hint: Each of the denominators contains a repeated linear factor.)
∫x−3(x+2)(x+1)2dx
−5ln|x+2|+5ln|x+1|+4x+1+C
∫x+1x2(x−2)dx
∫x2dx(x−1)2(x+1)
14ln|x+1|+34ln|x−1|−12(x−1)+C
∫x2+x(x+2)(x−1)2dx
In Problems 19–22, find each integral. (Hint: Each of the denominators contains an irreducible quadratic factor.)
∫dxx(x2+1)
ln|x|−12ln(x2+1)+C
∫dx(x+1)(x2+4)
∫x2+2x+3(x+1)(x2+2x+4)dx
16ln(x2+2x+4)+23ln|x+1|+C
∫x2−11x−18x(x2+3x+3)dx
In Problems 23–26, find each integral. (Hint: Each of the denominators contains a repeated irreducible quadratic factor.)
∫2x+1(x2+16)2dx
−1x2+16+1128tan−1x4+x32(x2+16)+C
∫x2+2x+3(x2+4)2dx
∫x3dx(x2+16)3
−12(x2+16)+4(x2+16)2+C
∫x2dx(x2+4)3
In Problems 27–36, find each integral.
∫xdxx2+2x−3
14ln|x−1|+34ln|x+3|+C
∫x2−x−8(x+1)(x2+5x+6)dx
∫10x2+2x(x−1)2(x2+2)dx
143ln|x−1|−4x−1−73ln(x2+2)+2√23tan−1√2x2+C
∫x+4x2(x2+4)dx
∫7x+3x3−2x2−3xdx
−ln|x|−ln|x+1|+2ln|x−3|+C
∫x5+1x6−x4dx
∫x2(x−2)(x−1)2dx
4ln|x−2|−3ln|x−1|+1x−1+C
∫x2+1(x+3)(x−1)2dx
∫2x+1x3−1dx
ln|x−1|−12ln(x2+x+1)+√33tan−1√3(2x+1)3+C
∫dxx3−8
In Problems 37–40, find each definite integral.
∫10dxx2−9
16ln12
∫42dxx2−25
∫3−2dx16−x2
18ln21
∫21dx9−x2
Applications and Extensions
In Problems 41–54, find each integral. (Hint: Make a substitution before using partial fraction decomposition.)
∫cosθsin2θ+sinθ−6dθ
15ln(2−sinθ)−15ln(sinθ+3)+C
∫sinxcos2x−2cosx−8dx
∫sinθcos3θ+cosθdθ
−ln|cosθ|+12ln(cos2θ+1)+C
∫4cosθsin3θ+2sinθdθ
∫ete2t+et−2dt
13ln|et−1|−13ln(et+2)+C
∫exe2x+ex−6dx
∫exe2x−1dx
12ln|ex−1|−12ln(ex+1)+C
∫dxex−e−x
∫dte2t+1
t−12ln(e2t+1)+C
∫dte3t+et
∫sinxcosx(sinx−1)2dx
ln|sinx−1|−1sinx−1+C
∫cosxsinx(cosx−2)2dx
∫cosx(sin2x+9)2dx
154tan−1sinx3+118sinxsin2x+9+C
∫sinx(cos2x+4)2dx
507
Area Find the area under the graph of y=4x2−4 from x=3 to x=5, as shown in the figure below.
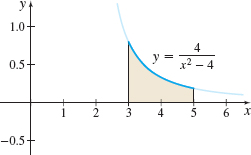
ln157
Area Find the area under the graph of y=x−4(x+3)2 from x=4 to x=6, as shown in the figure below.

Area Find the area under the graph of y=8x3+1 from x=0 to x=2, as shown in the figure below.
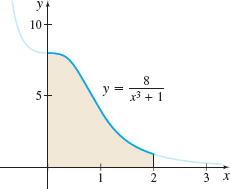
4π√33+43ln3
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of y=xx2−4 and the x-axis from x=3 to x=5 about the x -axis, as shown in the figure below.
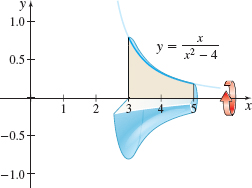
- (a) Find the zeros of q(x)=x3+3x2−10x−24.
- (b) Factor q.
- (c) Find the integral ∫3x−7x3+3x2−10x−24dx.
- (a) −4,−2,3
- (b) (x+4)(x+2)(x−3)
- (c) 1310ln|x+2|+235ln|x−3|−1914ln|x+4|+C
Challenge Problems
In Problems 60–71, simplify each integrand as follows: If the integrand involves fractional powers such as xp/q and xr/s, make the substitution x=un, where n is the least common denominator of pq and rs. Then find each integral.
∫xdx3+√x
∫dx√x+2
2√x−4ln(√x+2)+C
∫dxx−3√x
∫xdx3√x−1
35x5/3+34x4/3+32x2/3+x+3x1/3+3ln|x1/3−1|+C
∫dx√x+3√x
∫dx3√x−3√x
23x1/2+13x1/3+29x1/6+227ln|3x1/6−1|+C
∫dx3√2+3x
∫dx4√1+2x
23(2x+1)3/4+C
∫xdx(1+x)3/4
∫dx(1+x)2/3
3(1+x)1/3+C
∫3√x+13√x−1dx
∫dx√x(1+3√x)2
−3x1/6x1/3+1+3tan−1x1/6+C
Weierstrass Substitution In Problems 72–87, use the following substitution, called a Weierstrass substitution. If an integrand is a rational expression of sinx or cosx or both, the substitution z=tanx2−π2<x2<π2
or equivalently, sinx=2z1+z2cosx=1−z21+z2dx=2dz1+z2
will transform the integrand into a rational function of z.
∫dx1−sinx
∫dx1+sinx
−21+tanx2+C
∫dx1−cosx
∫dx3+2cosx
2√55tan−1(√55tanx2)+C
∫2dxsinx+cosx
∫dx1−sinx+cosx
−ln|1−tanx2|+C
∫sinx3+cosxdx
∫dxtanx−1
12ln|tan2x2+2tanx2−1|−12ln(tan2x2+1)−x2+C
∫dxtanx−sinx
∫secxtanx−2dx
√55ln|tanx2−√52+12|−√52ln|tanx2+√52+12|+C
∫cotx1+sinxdx
∫secx1+sinxdx
−12ln|tanx2−1|+12ln|tanx2+1|+1tanx2+1−1(tanx2+1)2+C
∫π/20dxsinx+1
∫π/3π/4cscx3+4tanxdx
13ln√33−13ln(√2−1)−415ln(√3+1)−415ln(4−√2)+415ln(3√2−2)+415ln(3−√33)
∫π/20cosx2−cosxdx
∫π/404dxtanx+1
π2+ln2
508
Use a Weierstrass substitution to derive the formula ∫cscxdx=ln√1−cosx1+cosx+C
Show that the result obtained in Problem 88 is equivalent to ∫cscxdx=ln|cscx−cotx|+C
See the Student Solutions Manual.
Since ddxtanh−1x=11−x2, we might expect that ∫32dx1−x2=tanh−13−tanh−12. Why is this incorrect? What is the correct result?
Show that the two formulas below are equivalent. ∫secxdx=ln|secx+tanx|+C∫secxdx=ln|1+tanx21−tanx2|+C[Hint:tanx2=sinx2cosx2=sin2(x2)sin(x2)cos(x2)=1−cosxsinx.]
See the Student Solutions Manual.
Use the methods of this section to find ∫dx1+x4. (Hint: Factor 1+x4 into irreducible quadratics.)
