7.8 Assess Your UnderstandingPrinted Page 530
530
Concepts and Vocabulary
Multiple Choice If a function f is continuous on the interval [a,∞), then ∫∞af(x)dx is called [(a) a definite,(b) an infinite, (c) an improper, (d) a proper ] integral.
(c)
Multiple Choice If the lim does not exist, the improper integral \int_{a}^{\infty }f(x)\,dx [ (a) converges, (b) diverges, (c) equals ab].
(b)
True or False If a function f is continuous for all x, then the improper integral \int_{-\infty }^{\,\infty }f(x)\,dx always converges.
False
True or False If a function f is continuous and nonnegative on the interval [a,\,\infty) , and \int_{a}^{\infty } f( x) \,dx converges, then \int_{a}^{\infty }f(x)\,dx represents the area under the graph of y=f(x) for x \ge a.
True
True or False If a function f is continuous for all x, then the improper integral \int_{-\infty }^{\infty }f(x)\,dx=\lim\limits_{a\,\rightarrow \,\infty }\int_{-a}^{a}f(x)\,dx.
False
To determine whether the improper integral \int_{a}^{b} f( x) \,dx converges or diverges, where f is continuous on [a,\,b), but is not defined at b, requires finding what limit?
\lim_{t\rightarrow b^{-}}\int_a^tf(x)dx
Skill Building
In Problems 7–14, determine whether each integral is improper. For those that are improper, state the reason.
\int_{0}^{\infty }x^{2}\,dx
Yes, \infty is a limit of integration.
\int_{0}^{5}x^{3}dx
\int_{2}^{3}\dfrac{dx}{x-1}
No
\int_{1}^{2}\dfrac{dx}{x-1}
\int_{0}^{1}\dfrac{1}{x}\,dx
Yes, the function is undefined at 0.
\int_{-1}^{1}\dfrac{x\, dx}{x^{2}+1}
\int_{0}^{1}\dfrac{x}{x^{2}-1}\,dx
Yes, the function is undefined at 1.
\int_{0}^{\infty }e^{-2x}\,dx
In Problems 15–24, determine whether each improper integral converges or diverges. If it converges, find its value.
\int_{1}^{\infty }\dfrac{dx}{x^{3}}
Converges to \dfrac{1}{2}.
\int_{-\infty }^{-10}\dfrac{dx}{x^{2}}
\int_{0}^{\infty }e^{2x}\,dx
Diverges
\int_{0}^{\infty }e^{-x}\,dx
\int_{-\infty }^{-1}\dfrac{4}{x}\,dx
Diverges
\int_{1}^{\infty }\dfrac{4}{x}\,dx
\int_{3}^{\infty }\dfrac{dx}{(x-1)^{4}}
Converges to \dfrac{1}{24}.
\int_{-\infty }^{0}\dfrac{dx}{(x-1) ^{4}}
\int_{-\infty }^{\infty }\dfrac{dx}{x^{2}+4}
Converges to \dfrac{\pi}{2}.
\int_{-\infty }^{\infty }\dfrac{dx}{x^{2}+1}
In Problems 25–32, determine whether each improper integral converges or diverges. If it converges, find its value.
\int_{0}^{1}\dfrac{dx}{x^{2}}
Diverges
\int_{0}^{1}\dfrac{dx}{x^{3}}
\int_{0}^{1}\dfrac{dx}{x}
Diverges
\int_{4}^{6}\dfrac{dx}{x-4}
\int_{0}^{4}\dfrac{dx}{\sqrt{4-x}}
Converges to 4.
\int_{1}^{5}\dfrac{x~dx}{\sqrt{5-x}}
\int_{-1}^{1}\dfrac{dx}{\sqrt[3]{x}}
Converges to 0.
\int_{0}^{3}\dfrac{dx}{(x-2)^{2}}
In Problems 33–62, determine whether each improper integral converges or diverges. If it converges, find its value.
\int_{0}^{\infty }\cos x\,dx
Diverges
\int_{0}^{\infty }\sin (\pi x) \,dx
\int_{-\infty }^{0}e^{x}\,dx
Converges to 1.
\int_{-\infty }^{0}e^{-x}\,dx
\int_{0}^{\pi /2}\dfrac{x\,dx}{\sin x^{2}}
Diverges
\int_{0}^{1}\dfrac{\ln x\,dx}{x}
\int_{0}^{1}\dfrac{dx}{1-x^{2}}
Diverges
\int_{1}^{2}\dfrac{dx}{\sqrt{x^{2}-1}}
\int_{0}^{1}\dfrac{x\,dx}{(1-x^{2})^{2}}
Diverges
\int_{0}^{2}\dfrac{dx}{(x-1)^{2}}
\int_{0}^{\pi /4}\tan (2x) \,dx
Diverges
\int_{0}^{\pi /2}\csc x\,dx
\int_{0}^{\infty }\dfrac{x\,dx}{\sqrt{x+1}}
Diverges
\int_{2}^{\infty }\dfrac{dx}{x\sqrt{x^{2}-1}}
\int_{-\infty }^{\infty }\dfrac{dx}{x^{2}+4x+5}
Converges to \pi.
\int_{-\infty }^{\infty }\dfrac{dx}{e^{x}+e^{-x}}
\int_{-\infty }^{2}\dfrac{dx}{\sqrt{4-x}}
Diverges
\int_{-\infty }^{1}\dfrac{x\,dx}{\sqrt{2-x}}
\int_{2}^{4}\dfrac{2x\,dx}{\sqrt[3]{x^{2}-4}}
Converges to 3\sqrt[3]{18}.
\int_{0}^{\pi }\dfrac{1}{1-\cos x}\,dx
\int_{-1}^{1}\dfrac{1}{x^{3}}\,dx
Diverges
\int_{0}^{2}\dfrac{dx}{x-1}
\int_{0}^{2}\dfrac{dx}{(x-1)^{1/3}}
Converges to 0.
\int_{-1}^{1}\dfrac{dx}{x^{5/3}}
\int_{1}^{2}\dfrac{dx}{(2-x)^{3/4}}
Converges to 4.
\int_{0}^{4}\dfrac{dx}{\sqrt{8x-x^{2}}}
\int_{a}^{3a}\dfrac{2x\,dx}{(x^{2}-a^{2})^{3/2}}, a \gt 0
Diverges
\int_{0}^{3}\dfrac{x\,dx}{(9-x^{2})^{3/2}}
\int_{0}^{\infty }xe^{-x^{2}}\,dx
Converges to \dfrac{1}{2}.
\int_{0}^{\infty }e^{-x}\sin x\,dx
In Problems 63–70:
- (a) Use the Comparison Test for Improper Integrals to determine whether each improper integral converges or diverges. (Hint: Use the fact that \int_{1}^{\infty }\dfrac{dx}{x^{p}} converges if p \gt1 and diverges if p \le 1.)
- (b)
 If the integral converges, use a CAS to find its value.
If the integral converges, use a CAS to find its value.
\int_{1}^{\infty }\dfrac{1}{\sqrt{x^{2}-1}}\,dx
Diverges
\int_{2}^{\infty }\dfrac{2}{\sqrt{x^{2}-4}}\,dx
\int_{1}^{\infty }\dfrac{1+e^{-x}}{x}\,dx
Diverges
\int_{1}^{\infty }\dfrac{3e^{-x}}{x}\,dx
\int_{1}^{\infty }\dfrac{\sin ^{2}x}{x^{2}}\,dx
- (a) Converges
- (b) \approx 0.673
\int_{1}^{\infty }\dfrac{\cos ^{2}x}{x^{2}}\,dx
\int_{1}^{\infty }\dfrac{dx}{(x+1) \sqrt{x}}
- (a) Converges
- (b) \dfrac{\pi}{2}
\int_{1}^{\infty }\dfrac{dx}{x\sqrt{1+x^{2}}}
531
Applications and Extensions
Area Between Graphs Find the area, if it is defined, of the region enclosed by the graphs of y=\dfrac{1}{x+1} and y=\dfrac{1}{x+2} on the interval [0,\infty ). See the figure.
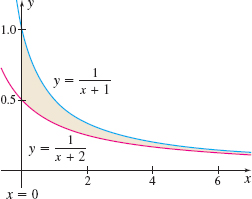
\ln 2
Area Between Graphs Find the area, if it is defined, under the graph of y=\dfrac{1}{1+x^{2}} to the right of x=0. See the figure below.
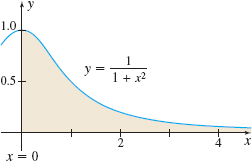
Volume of a Solid of Revolution Find the volume, if it is defined, of the solid of revolution generated by revolving the region bounded by the graph of y=e^{-x} and the x-axis to the right of x=0 about the x-axis. See the figure below.
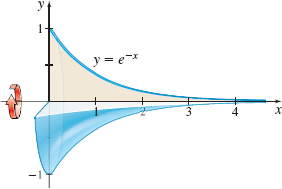
\dfrac{\pi}{2}
Volume of a Solid of Revolution Find the volume, if it is defined, of the solid of revolution generated by revolving the region bounded by the graph of y=\dfrac{1}{\sqrt{x}} and the x-axis to the right of x=1 about the x-axis. See the figure below.
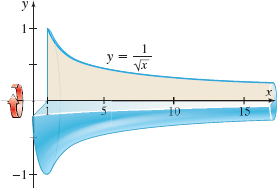
Area Between Graphs Find the area, if it is defined, between the graph of y=\dfrac{8a^{3}}{x^{2}+4a^{2}}, a>0, and its horizontal asymptote.
4\pi a^2
Drug Reaction The rate of reaction r to a given dose of a drug at time t hours after administration is given by r(t)=t\,e^{-t^{2}} (measured in appropriate units).
- (a) Why is it reasonable to define the total reaction as the area under the graph of y=r(t) on [0,\infty) ?
- (b) Find the total reaction to the given dose of the drug.
Present Value of Money The present value PV of a capital asset that provides a perpetual stream of revenue that flows continuously at a rate of R(t) dollars per year is given by PV= \int_{0}^{\infty }R(t)e^{-rt}\,dt
where r, expressed as a decimal, is the annual rate of interest compounded continuously.
- (a) Find the present value of an asset if it provides a constant return of \$100 per year and r=8\%.
- (b) Find the present value of an asset if it provides a return of R(t)=1000+80t dollars per year and r=7\%.
- (a) $1250
- (b) $30,612
Electrical Engineering In a problem in electrical theory, the integral \int_{0}^{\infty }Ri^{2}\,dt occurs, where the current i=Ie^{-Rt/L}, t is time, and R, I, and L are positive constants. Find the integral.
Magnetic Potential The magnetic potential u at a point on the axis of a circular coil is given by u=\dfrac{2\pi NIr}{10}\! \int_{x}^{\infty }\dfrac{dy}{(r^{2}+y^{2})^{3/2}}
where N, I, r, and x are constants. Find the integral.
\dfrac{\pi N I}{5r}\left(1-\dfrac{x}{\sqrt{r^2+x^2}}\right)
Electrical Engineering The field intensity F around a long (“infinite”) straight wire carrying electric current is given by the integral F=\dfrac{rIm}{10}\int_{-\infty }^{\infty }\dfrac{dy}{(r^{2}+y^{2})^{3/2}}
where r, I, and m are constants. Find the integral.
Work The force F of gravitational attraction between two point masses m and M that are r units apart is F=\dfrac{GmM}{r^{2}} , where G is the universal gravitational constant. Find the work done in moving the mass m along a straight-line path from r=1 unit to r=\infty .
GmM
For what numbers a does \int_{0}^{1}x^{a}\,dx converge?
In Problems 83–86, use integration by parts and perhaps L'Hôpital's Rule to find each improper integral.
\int_{0}^{\infty }xe^{-x}\,dx
1
\int_{0}^{1}x\ln x\,dx
\int_{0}^{\infty}e^{-x}\cos x\,dx
\dfrac{1}{2}
\int_{0}^{\infty }\tan^{-1}x\,dx
Show that \int_{0}^{\infty }\sin x\,dx and \int_{-\infty }^{0}\sin x\,dx each diverge, yet \lim\limits_{t\,\rightarrow \,\infty }\int_{-t}^{t}\sin x\, dx=0.
See the Student Solutions Manual.
532
Find a function f for which \int_{0}^{\infty }f(x)\,dx and \int_{-\infty }^{0}f(x)\,dx each diverge, yet \lim\limits_{t\,\rightarrow \,\infty }\int_{-t}^{t}f(x)\,dx=1.
Use the Comparison Test for Improper Integrals to show that \int_{0}^{\infty }\dfrac{1}{\sqrt{2+\sin x}}\,dx diverges.
See the Student Solutions Manual.
Use the Comparison Test for Improper Integrals to show that \int_{2}^{\infty }\dfrac{\ln x}{\sqrt{x^{2}-1}}\,dx diverges.
If n is a positive integer, show that:
- (a) \int_{0}^{\infty }x^{n}\,e^{-x}\,dx=n\int_{0}^{\infty }x^{n-1}\,e^{-x}\,dx
- (b) \int_{0}^{\infty }x^{n}\,e^{-x}\,dx=n!
See the Student Solutions Manual.
Show that \int_{e}^{\infty }\dfrac{\,dx}{x ( \ln x) ^{p}} converges if p \gt 1 and diverges if p \le 1.
Show that \int_{a}^{b}\dfrac{dx}{(x-a) ^{p}} converges if 0 \lt p \lt 1 and diverges if p \ge 1.
See the Student Solutions Manual.
Show that \int_{a}^{b}\dfrac{dx}{(b-x)^{p}} converges if 0 \lt p \lt 1 and diverges if p \ge 1.
Refer to Problems 93 and 94. Discuss the convergence or divergence of the integrals if p \le 0. Support your explanation with an example.
See the Student Solutions Manual.
Comparison Test for Improper Integrals Show that if two functions f and g are nonnegative and continuous on the interval [ a,\infty ) , and if f( x) \geq g( x) for all numbers x > c, where c \geq a, then
- If \int_{a}^{\infty }f( x)\, dx converges, then \int_{a}^{\infty }g( x)\,dx also converges.
- If \int_{a}^{\infty }g( x)\, dx diverges, then \int_{a}^{\infty }f( x)\, dx also diverges.
Laplace transforms are useful in solving a special class of differential equations. The Laplace transform L {f( x)} of a function f is defined as L \{f( x)\} =\int_{0}^{\infty }e^{-sx} f(x) \,dx, x \ge 0, s \hbox{ a complex number }
In Problems 97–102, find the Laplace transform of each function.
f(x) =x
\dfrac{1}{s^2}
f(x) =\cos x
f(x) =\sin x
\dfrac{1}{s^{2}+1}
f(x) =e^{x}
f(x) =e^{ax}
\dfrac{1}{s-a}
f(x) =1
Challenge Problems
Find the arc length of y=\sqrt{x-x^{2}}-\sin ^{-1}\sqrt{x}.
2
Find \int_{-\infty }^{a}e^{(x-e^{x})}\,dx.
Find \int_{-\infty }^{\infty }e^{(x-e^{x})}\,dx.
1
- (a) Show that the area of the region in the first quadrant bounded by the graph of y=e^{-x} and the x-axis is divided into two equal parts by the line x=\ln 2.
- (b) If the two regions with equal areas described in (a) are rotated about the x-axis, are the resulting volumes equal? If they are unequal, which one is larger and by how much?
In Problems 107 and 108, use the following definition: A probability density function is a function f, whose domain is the set of all real numbers, with the following properties:
- f(x) \ge 0 for all x
- \int_{-\infty }^{\infty }f(x)\,dx=1
Uniform Density Function Show that the function f below is a probability density function. f(x)=\left\{ \begin{array}{c@{\qquad}l@{\quad}rl} 0 & \hbox{if} & x& \lt a \\ \dfrac{1}{b-a} & \hbox{if} & a & \le x \le b, a \lt b \\ 0 & \hbox{if} & x& \gt b \end{array} \right.
See the Student Solutions Manual.
Exponential Density Function Show that the function f is a probability density function for a>0. f(x)=\left\{ \begin{array}{l@{\qquad}l@{\quad}ll} \dfrac{1}{a}e^{-x/a} & \hbox{if}&x & \ge 0 \\ 0&\hbox{if}&x & \lt 0 \end{array} \right.
In Problems 109 and 110, use the following definition: The expected value or mean \mu associated with a probability density function f is defined by \mu =\int_{-\infty }^{\infty }x f(x)\,dx
The expected value can be thought of as a weighted average of its various probabilities.
Find the expected value \mu of the uniform density function f given in Problem 107.
\dfrac{a+b}{2}
Find the expected value \mu of the exponential probability density function f defined in Problem 108.
In Problems 111 and 112, use the following definitions: The variance \sigma ^{2} of a probability density function f is defined as \sigma ^{2}=\int_{-\infty }^{\infty }(x-\mu )^{2} f(x)\,dx The variance is the average of the squared deviation from the mean. The standard deviation \sigma of a probability density function f is the square root of its variance \sigma ^{2}.
Find the variance \sigma ^{2} and standard deviation \sigma of the uniform density function defined in Problem 107.
\sigma^2=\dfrac{(b-a)^2}{12}, \sigma=\dfrac{b-a}{2\sqrt{3}}
Find the variance \sigma ^{2} and standard deviation \sigma of the exponential density function defined in Problem 108.
