7.1 Assess Your UnderstandingPrinted Page 478
Concepts and Vocabulary
True or False Integration by parts is based on the Product Rule for derivatives.
True
The integration by parts formula states that ∫udv= ______.
uv−∫vdu
Skill Building
In Problems 3–30, use integration by parts to find each integral.
∫xe2xdx
12xe2x−14e2x+C
∫xe−3xdx
∫xcosx dx
xsinx+cosx+C
∫xsin(3x) dx
∫√xlnx dx
23x3/2 lnx−49x3/2+C
∫x−2lnx dx
∫cot−1x dx
xcot−1x+12ln(x2+1)+C
∫sin−1x dx
∫(lnx)2dx
x(lnx)2−2xlnx+2x+C
∫x(lnx)2dx
∫x2sinx dx
−x2cosx+2xsinx+2cosx+C
∫x2cosx dx
∫xcos2x dx
12xcosxsinx+14x2−14sin2x+C
∫xsin2x dx
∫xsinhx dx
xcoshx−sinhx+C
∫xcoshx dx
∫cosh−1x dx
xcosh−1x−√x2−1+C
∫sinh−1x dx
∫sin(lnx) dx
x2[sin(lnx)−cos(lnx)]+C
∫cos(lnx) dx
∫(lnx)3dx
x(lnx)3−3x(lnx)2+6xlnx−6x+C
∫(lnx)4dx
∫x2(lnx)2dx
13x3(lnx)2−29x3lnx+227x3+C
∫x3(lnx)2dx
∫x2tan−1x dx
13x3tan−1x−16x2+16ln(1+x2)+C
∫xtan−1x dx
∫7xx dx
7xxln7−7x(ln7)2+C
∫2−xx dx
In Problems 31–38, use integration by parts to find each definite integral.
∫π0excosx dx
−eπ+12
∫10x2e−xdx
∫20x2e−3xdx
227−5027e−6
∫π/40xtan2x dx
∫91ln√xdx
9ln3−4
∫3π/4π/4xcsc2x dx
∫e1(lnx)2dx
e−2
∫π/40xsec2x dx
Applications and Extensions
Area Between Two Graphs In Problems 39 and 40, find the area of the region enclosed by the graphs of f and g.
f(x)=3lnx and g(x)=xlnx,x≥1
92ln3−4
f(x)=4xlnx and g(x)=x2lnx,x≥1
Area Under a Graph Find the area under the graph of y=exsinx from 0 to π.
eπ+12
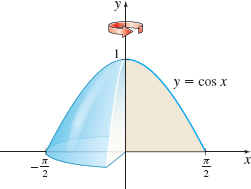
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of y=cosx and the x-axis from x=0 to x=π2 about the y-axis. See the figure below.
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of y=sinx and the x-axis from x=0 to x=π2 about the y-axis.
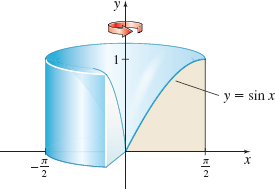
2π
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of y=x√sinx and the x-axis from x=0 to x=π2 about the x-axis.
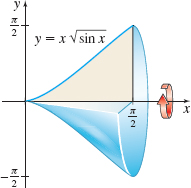
479
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of y=lnx and the x-axis from x=1 to x=e about the x-axis.
eπ−2π
 Area
Area- (a) Graph the functions f(x)=x3e−3x and g(x)=x2e−3x on the same set of coordinate axes.
- (b) Find the area enclosed by the graphs of f and g.
 Damped Spring The displacement x of a damped spring at time t, 0≤t≤5, is given by x=x(t)=3e−tcos(2t)+2e−tsin(2t).
Damped Spring The displacement x of a damped spring at time t, 0≤t≤5, is given by x=x(t)=3e−tcos(2t)+2e−tsin(2t).- (a) Graph x=x(t).
- (b) Find the least positive number t that satisfies x(t)=0.
- (c) Find the area under the graph of x=x(t) from t=0 to the value of t found in (b).
- (a)
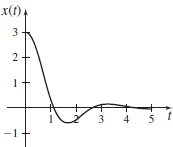
- (b) π2+12tan−1(−32)
- (c) ≈1.890
A function y=f(x) is continuous and differentiable on the interval (2,6). If ∫53f(x) dx=18 and f(3)=8 and f(5)=11, then find ∫53xf′(x) dx.
In Problems 49–54, find each integral by first making a substitution and then integrating by parts.
∫sin√xdx
2sin√x−2√xcos√x+C
∫e√xdx
∫cosxln(sinx) dx
(sinx)ln(sinx)−sinx+C
∫exln(2+ex)dx
∫e4xcose2xdx
12e2xsine2x+12cose2x+C
∫cosxtan−1(sinx) dx
Find ∫x3ex2dx. (Hint: Let u=x2,dv=xex2dx.)
12x2ex2−12ex2+C
Find ∫xnlnx dx; n≠−1, n real.
Find ∫xexcosx dx.
12ex(xsinx+xcosx−sinx)+C
Find ∫xexsinx dx.
In Problems 59–62, derive each reduction formula where n>1 is an integer.
∫xnsin−1xdx=xn+1n+1sin−1x−1n+1∫xn+1√1−x2dx
See the Student Solutions Manual.
∫dx(x2+1)n+1=(1−12n)∫dx(x2+1)n+x2n(x2+1)n
∫sinnx dx=−sinn−1xcosxn+n−1n∫sinn−2xdx
See the Student Solutions Manual.
∫sinnxcosmx dx=−sinn−1xcosm+1xn+m+n−1n+m∫sinn−2xcosmxdx
where m≠−n, m≠−1
- (a) Find ∫x2e5xdx.
- (b) Using integration by parts, derive a reduction formula for ∫xnekxdx, where k≠0 and n≥2 is an integer, in which the resulting integrand involves xn−1.
- (a) 15x2e5x−225xe5x+2125e5x+C
- (b) ∫xnekxdx=1kxnekx−nk∫xn−1ekxdx
- (a) Assuming there is a function p for which ∫x3exdx =p(x)ex, show that p(x)+p′(x)=x3.
- (b) Use integration by parts to find a polynomial p of degree 3 for which ∫x3exdx=p(x)ex+C.
- (a) Use integration by parts with u=sinx and dv=cosxdx to find a function f for which ∫sinxcosx dx=f(x)+C1.
- (b) Use integration by parts with u=cosx and dv=sinxdx to find a function g for which ∫sinxcosx dx=g(x)+C2.
- (c) Use the trigonometric identity sin(2x)=2sinxcosx and substitution to find a function h for which ∫sinxcosx dx=h(x)+C3.
- (d) Compare the functions f and g. Find a relationship between C1 and C2.
- (e) Compare the functions f and h. Find a relationship between C1 and C3.
- (a) f(x)=12sin2x
- (b) g(x)=−12cos2x
- (c) h(x)=−14cos(2x)
- (d) C2=12+C1
- (e) C3=14+C1
Derive the formula ∫ln(x+√x2+a2)dx=xln(x+√x2+a2)−√x2+a2+C
Derive the formula ∫eaxsin(bx) dx=eax[asin(bx)−bcos(bx)]a2+b2+C,a>0,b>0
See the Student Solutions Manual.
Suppose F(x)=∫x0tg′(t)dt for all x≥0. Show that F(x)= xg(x)−∫x0g(t)dt.
Use Wallis’ formulas, given below, to find each definite integral.
- ∫π/20sinnx dx=∫π/20cosnx dx n>1 an integer ={(n−1)(n−3)⋯(4)(2)n(n−2)⋯(5)(3)(1)n>1 is odd(n−1)(n−3)⋯(5)(3)(1)n(n−2)⋯(4)(2)(π2)n>1 is even
- (a) ∫π/20sin6x dx
- (b) ∫π/20sin5x dx
- (c) ∫π/20cos8x dx
- (d) ∫π/20cos6x dx
- (a) 5π32
- (b) 815
- (c) 35π256
- (d) 5π32
Challenge Problems
Derive Wallis’ formulas given in Problem 69. (Hint: Use the result of Problem 61.)
- (a) If n is a positive integer, use integration by parts to show that there is a polynomial p of degree n for which ∫xnexdx=p(x)ex+C
480
- (b) Show that p(x)+p′(x)=xn.
- (c) Show that p can be written in the form p(x)=n∑k=0(−1)kn!(n−k)!xn−k
- (a) If n is a positive integer, use integration by parts to show that there is a polynomial p of degree n for which ∫xnexdx=p(x)ex+C
See the Student Solutions Manual.
Show that for any positive integer n, ∫10ex2dx=e⋅[1−23+415−8105+⋯+(−1)n2n(2n+1)(2n−1)⋯3⋅1]+(−1)n+1⋅2n+1(2n+1)(2n−1)⋯3⋅1∫10x2n+2ex2dx
Use integration by parts to show that if f is a polynomial of degree n≥1, then ∫f(x)exdx=g(x)ex+C for some polynomial g(x) of degree n.
See the Student Solutions Manual.
Start with the identity f(b)−f(a)=∫baf′(t)dt and derive the following generalizations of the Mean Value Theorem for Integrals:
- (a) f(b)−f(a)=f′(a)(b−a)−∫baf′′(t)(t−b)dt
- (b) f(b)−f(a)=f′(a)(b−a)+f′′(a)2(b−a)2+∫baf′′′(t)2(t−b)2dt
If y=f(x) has the inverse function given by x=f−1(y), show that ∫baf(x)dx+∫f(b)f(a)f−1(y)dy=bf(b)−af(a)
See the Student Solutions Manual.
- (a) When integration by parts is used to find ∫excoshx dx, what happens? Explain.
- (b) Find ∫excoshx dx without using integration by parts.
