7.3 Assess Your UnderstandingPrinted Page 493
Concepts and Vocabulary
True or False To find ∫√a2−x2dx, the substitution x=asinθ, −π2≤θ≤π2, can be used.
True
Multiple Choice To find ∫√x2+16dx, use the substitution x=[(a) 4sinθ, (b) tanθ, (c) 4secθ, (d) 4tanθ].
(d)
Multiple Choice To find ∫√x2−9dx, use the substitution x=[(a) secθ, (b) 3sinθ, (c) 3secθ, (d) 3tanθ].
(c)
Multiple Choice To find ∫√25−4x2dx, use the substitution x=[(a) 52tanθ, (b) 52sinθ, (c) 25sinθ, (d) 25secθ].
(b)
494
Skill Building
In Problems 5–14, find each integral. Each of these integrals contains a term of the form √a2−x2.
∫√4−x2dx
x2√4−x2+2sin−1x2+C
∫√16−x2dx
∫x2√16−x2dx
−x2√16−x2+8sin−1x4+C
∫x2√36−x2dx
∫√4−x2x2dx
−1x√4−x2−sin−1x2+C
∫√9−x2x2dx
∫x2√4−x2dx
x(x2−2)4√4−x2+2sin−1x2+C
∫x2√1−16x2dx
∫dx(4−x2)3/2
14x√4−x2+C
∫dx(1−x2)3/2
In Problems 15–26, find each integral. Each of these integrals contains a term of the form √x2+a2.
∫√4+x2dx
12x√4+x2+2ln|√4+x2+x2|+C
∫√1+x2dx
∫dx√x2+16
ln|√x2+16+x4|+C
∫dx√x2+25
∫√1+9x2dx
x2√1+9x2+16ln|√1+9x2+3x|+C
∫√9+4x2dx
∫x2√4+9x2dx
118x√4+9x2−227ln|√4+9x2+3x2|+C
∫x2√x2+16dx
∫dxx2√x2+4
−√x2+44x+C
∫dxx2√4x2+1
∫dx(x2+4)3/2
x4√x2+4+C
∫dx(x2+1)3/2
In Problems 27–36, find each integral. Each of these integrals contains a term of the form √x2−a2.
∫x2√x2−25dx
x2√x2−25+252ln|x+√x2−255|+C
∫x2√x2−16dx
∫√x2−1xdx
√x2−1−sec−1x+C
∫√x2−1x2dx
∫dxx2√x2−36
√x2−3636x+C
∫dxx2√x2−9
∫dx√4x2−9
12ln|2x+√4x2−93|+C
∫dx√9x2−4
∫dx(x2−9)3/2
−19x√x2−9+C
∫dx(25x2−1)3/2
In Problems 37–48, find each integral.
∫x2dx(x2−9)3/2
−x√x2−9+ln|x+√x2−93|+C
∫x2dx(x2−4)3/2
∫x2dx16+x2
x−4tan−1x4+C
∫x2dx1+16x2
∫√4−25x2dx
x2√4−25x2+25sin−15x2+C
∫√9−16x2dx
∫dx(4−25x2)3/2
x4√4−25x2+C
∫dx(1−9x2)3/2
∫√4+25x2dx
12x√4+25x2+25ln|√4+25x2+5x2|+C
∫√9+16x2dx
∫dxx3√x2−16
1128sec−1x4+√x2−1632x2+C
∫dxx3√x2−1
In Problems 49–58, find each definite integral.
∫10√1−x2dx
π4
∫1/20√1−4x2dx
∫10√1+x2dx
√2+ln(1+√2)2
∫20x2√9+x2dx
∫54x2√x2−9dx
10−2√7+9ln3−92ln(4+√7)
∫21x2√4x2−1dx
∫20x2dx(16−x2)3/2
√33−π6
∫10x2dx(25−x2)3/2
∫30x2dx9+x2
3−3π4
∫10x225+x2dx
Applications and Extensions
Area of an Ellipse Find ∫√a2−x2dx and use it to find the area enclosed by the ellipse x2a2+y2b2=1.
πab
Area of a Semicircle
- (a) Find ∫20√4−x2dx by interpreting the integral as a certain area and using elementary geometry.
- (b) Find ∫20√4−x2dx using a trigonometric substitution.
- (c) Find the area of the semicircle y=√a2−x2,−a≤x≤a, using integration.
Average Value Find the average value of the function f(x)=1√9−4x2 over the interval [0,1].
12sin−123
Average Value Find the average value of the function f(x)=√x2−4 the interval [2,7].
Area Under a Graph Find the area under the graph of y=x3√9−x2 from x=0 to x=2.
18−22√53
Area Under a Graph Find the area under the graph of y=x√16−x2,x≥0.
495
Area Under a Graph Find the area under the graph of y=x2√x2−1from x=3 to x=5.
12ln(2√6+5)−12ln(2√2+3)−3√2+5√6
Hydrostatic Force A round window of radius 2 meters ( m) is built into the side of a large, fresh-water aquarium tank. If the center of the window is 3m below the water line, find the force due to hydrostatic pressure on the window. (Hint: The mass density of fresh water is ρ=1000kg/m3.)
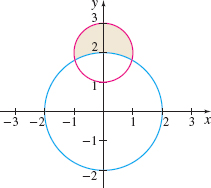
Area of a Lune A lune is a crescent-shaped area formed when two circles intersect.
- (a) Find the area of the smaller lune formed by the intersection of the two circles x2+y2=4 and x2+(y−2)2=1, as shown in the figure.
- (b) What is the area of the larger lune?
- (a) 4sin−1√158+sin−1√154−√152
- (b) π−4sin−1√158−sin−1√154+√152
Area Find the area enclosed by the hyperbola x29−y216=1 and the line x=6.
Arc Length Find the length of the graph of the parabola y=5x−x2that lies above the x-axis.
14ln(√26+5)−14ln(√26−5)+52√26
Arc Length Find the length of the graph of y=lnx from x=√33 to x=√3.
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of y=1x2+4 and the x-axis from x=0 to x=1 about the x -axis. See the figure.
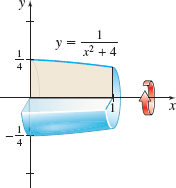
π40+π16tan−112
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graphs of y=1√9−x2, y=0, x=0, and x=2 about the x-axis.
In Problems 73–78, find each integral. (Hint: Begin with a substitution.)
∫dx√1−(x−2)2
sin−1(x−2)+C
∫√4−(x+2)2dx
∫dx√(x−1)2−4
ln|x−1+√(x−1)2−4|+C
∫dx(x−2)√(x−2)2+9
∫ex√25−e2xdx
252sin−1ex5+12ex√25−e2x+C
∫ex√4+e2xdx
In Problems 79 and 80, use integration by parts and then the methods of this section to find each integral.
∫xsin−1xdx
12x2sin−1x−14sin−1x+14x√1−x2+C
∫xcos−1xdx
Find ∫√x2+a2dx
- (a) By using a trigonometric substitution
- (b) By using substitution with a hyperbolic function
- (a) x2√x2+a2+a22ln|x+√x2+a2a|+C
- (b) x2√x2+a2+a22sinh−1xa+C
In Problems 82–86, use a trigonometric substitution to derive each formula. Assume a>0.
∫dx√a2−x2=sin−1xa+C
∫dxa2+x2=1atan−1xa+C
See the Student Solutions Manual.
∫dxx√x2−a2=1asec−1xa+C
∫dx√x2−a2=ln|x+√x2−a2a|+C
See the Student Solutions Manual.
∫dx√x2+a2=ln|x+√x2+a2|+C
Challenge Problems
Find ∫dx√3x−x2
sin−12x−33+C
Derive the formula ∫√x2−a2dx=12x√x2−a2−12a2ln|x+√x2−a2|+C,a>0.
Find ∫dx√x2+a2, a>0, using the substitution u=sinh−1xa. Express your answer in logarithmic form.
lnx+√x2+a2a+C
Find ∫sec2x√tan2x−6tanx+8dx.
