8.5 Alternating Series; Absolute Convergence
582
OBJECTIVES
When you finish this section, you should be able to:
- Determine whether an alternating series converges (p. 583)
- Approximate the sum of a convergent alternating series (p. 584)
- Determine whether a series converges (p. 586)
In Sections 8.3 and 8.4, the series have only positive terms. We now investigate series that have some positive and some negative terms. The properties of series with positive terms often help to explain the properties of series that include terms with mixed signs.
The most common series with both positive and negative terms are alternating series, in which the terms alternate between positive and negative.
spanDEFINITIONspan Alternating Series
An alternating series is a series either of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] {\sum\limits_{k = 1}^\infty {{{\left( { - 1} \right)}^{k + 1}}{a_k} = {a_1} - {a_2} + {a_3} - {a_4} + \cdots }}} \]
or of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] {\sum\limits_{k = 1}^\infty {{{\left( { - 1} \right)}^{k}}{a_k} = {a_1} + {a_2} - {a_3} + {a_4} - \cdots }}} \]
where \(a_{k}>0\) for all integers \(k\geq 1\).
Two examples of alternating series are \[ 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots = \sum\limits_{k\, = \,1}^\infty {\frac{{{{( - 1)}^{k + 1}}}}{k}} \quad {\rm{and}}\quad - 1 + \frac{1}{{3!}} - \frac{1}{{5!}} + \frac{1}{{7!}}\ - \cdots = \sum\limits_{k\, = 1}^\infty {\frac{{{{( - 1)}^k}}}{{\left( {2k - 1} \right)!}}} \]
To determine whether an alternating series converges, we use the Alternating Series Test.
THEOREM Alternating Series Test
If the numbers \(a_{k},\) where \(a_{k}>0,\) of an alternating series \[ \sum_{k\,=\,1}^{\infty }(-1)^{k+1}a_{k}=a_{1}-a_{2}+a_{3}-a_{4}+\cdots \]
satisfy the two conditions:
- \(\lim\limits_{n\,\rightarrow \,\infty }\,a_{n}=0\)
- the \(a_{k}\) are nonincreasing; that is, \(a_{1}\geq a_{2}\geq a_{3}\geq \cdots \geq a_{n}\geq a_{n+1}\geq \cdots\)
then the alternating series converges.
NOTE
The Alternating Series Test is credited to Leibniz and is often called the Leibniz Test or Leibniz Criterion. The test also works if the \(a_{k}\) are eventually nonincreasing.
Proof
First consider partial sums with an even number of terms, and group them into pairs: \[ S_{2n} = a_{1} - a_{2} + a_{3}-a_{4} + \cdots +a_{2n-1} - a_{2n} = (a_{1} - a_{2}) + (a_{3} - a_{4}) + \cdots + (a_{2n-1} - a_{2n}) \]
Since \(a_{1}\geq a_{2}\geq a_{3}\geq a_{4}\geq ~\cdots \,\geq a_{2n-1}\geq a_{2n}\geq a_{2n+1}\geq \cdots\), the difference within each pair of parentheses is either \(0\) or positive. So, the sequence \(\{S_{2n}\}\) of partial sums is nondecreasing. That is, \begin{equation*} S_{2}\leq S_{4}\leq S_{6}\leq \cdots \leq S_{2n}\leq S_{2n+2}\leq \cdots \tag{1} \end{equation*}
583
For partial sums with an odd number of terms, group the terms a little differently, and write \[\begin{array}{l} {S_{2n + 1}} = {a_1} - {a_2} + {a_3} - {a_4} + {a_5} - \cdots - {a_{2n}} + {a_{2n + 1}} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {a_1} - ({a_2} - {a_3}) - ({a_4} - {a_5}) - \cdots - ({a_{2n}} - {a_{2n + 1}}) \\ \\ \end{array}\]
Again, the difference within each pair of parentheses is either \(0\) or positive. But this time the difference is subtracted from the previous term, so the sequence \(\{S_{2n+1}\}\) of partial sums is nonincreasing. That is, \begin{equation*} S_{1}\geq S_{3}\geq S_{5}\geq \cdots \geq S_{2n-1}\geq S_{2n+1}\geq \cdots \tag{2} \end{equation*} Now, since \(S_{2n+1}-S_{2n}=a_{2n+1}>0,\) we have \begin{equation*} S_{2n}<S_{2n+1} \tag{3} \end{equation*} Combine (1), (2), and (3) as follows: \[ \underset{{\color{#0066A7}{(3)}}}{\underbrace{\hspace{-4.5pc}{\underset{{\color{#0066A7}{(1)}}}{\underbrace{S_{2}\leq S_{4}\leq S_{6}\leq \cdots \leq S_{2n}}} \,<\, \underset{{\color{#0066A7}{(2)}}}{\underbrace{S_{2n+1}\leq \cdots \leq S_{5}\leq S_{3}\leq S_{1}}}}\hspace{-4.8pc}}} \]
Figure 23 shows the sequences \(S_{2n}\) and \(S_{2n+1}\).
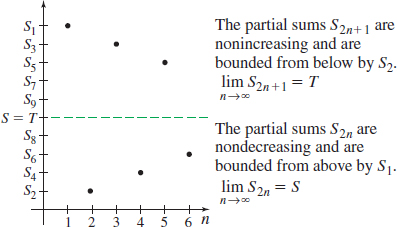
RECALL
A bounded, monotonic sequence converges.
The sequence \(S_{2},\) \(S_{4}, S_{6},\ldots\) is nondecreasing and bounded above by \(S_{1}\). So, this sequence has a limit; call it \(T\). Similarly, the sequence \(S_{1}, S_{3}, S_{5},\ldots\) is nonincreasing and is bounded from below by \(S_{2}\), so it, too, has a limit; call it \(S\). Since \(S_{2n+1}-S_{2n}=a_{n+1},\) we have \[ S-T=\lim\limits_{n\rightarrow \infty }S_{2n+1}-\lim_{n\,\rightarrow \,\infty }S_{2n}=\lim\limits_{n\rightarrow \infty }\left( S_{2n+1}-S_{2n}\right) =\lim\limits_{n\rightarrow \infty }a_{2n+1} \]
Since \(\lim\limits_{n\,\rightarrow \,\infty }a_{2n+1}=0\), we find \(S-T=0\). This means that \(S=T\), and the sequences \(\left\{S_{2n}\right\}\) and \(\{S_{2n+1}\}\) both converge to \(S\). It follows that \[ \lim\limits_{n\rightarrow \infty }~S_{n}=S \]
and so the alternating series converges.
1 Determine Whether an Alternating Series Converges
Showing an Alternating Series Converges
Show that the alternating harmonic series \(\sum\limits_{k=1}^{\infty }\dfrac{(-1)^{k+1}}{k}=1-\dfrac{1}{2}+\dfrac{1}{3} -\dfrac{1}{4}+\cdots\) converges.
Solution We check the two conditions of the Alternating Series Test. Since \(\lim\limits_{n\,\rightarrow \,\infty} a_{n}=\lim\limits_{n\,\rightarrow \,\infty }\dfrac{1}{n}=0,\) the first condition is met. Since \(a_{n+1}=\dfrac{1}{n+1}<\dfrac{1}{n}=a_{n}\), the \(a_{n}\) are nonincreasing, so the second condition is met. By the Alternating Series Test, the series converges.
NOTE
In Section 8.9 we show that the sum of the alternating harmonic series is \(\ln 2\).
NOW WORK
Problem 7.
584
When using the Alternating Series Test, we check the limit of the \(n\)th term first. If \(\lim\limits_{n\,\rightarrow \,\infty }\,a_{n}\neq 0\), the Test for Divergence tells us immediately that the series diverges. For example, in testing the alternating series \[ \sum_{k=2}^{\infty }(-1)^{k}\frac{k}{k-1}=2-\frac{3}{2}+\frac{4}{3}-\frac{5}{4}+\cdots\ \]
we find \(\lim\limits_{n\,\rightarrow \,\infty}\,a_{n}=\lim\limits_{n\,\rightarrow \,\infty }\,\dfrac{n}{n-1}=1\). There is no need to look further. By the Test for Divergence, the series diverges.
If \(\lim\limits_{n\rightarrow \infty }a_{n}=0,\) then check whether the terms \(a_{k}\) are nonincreasing. Recall there are three ways to verify if the \(a_{k}\) are nonincreasing:
- Use the Algebraic Difference test and show that \(a_{n+1}-a_{n}\leq 0\) for all \(n\geq 1\).
- Use the Algebraic Ratio test and show that \(\dfrac{a_{n+1}}{a_{n}}\leq 1\) for all \(n\geq 1\).
- Use the derivative of the related function \(f\), defined for \(x>0\) and for which \(a_{n}=f(n)\) for all \(n\), and show that \(f^\prime (x) \leq 0\) for all \(x>0\).
Showing an Alternating Series Converges
Show that the alternating series \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{(-1)^{k}}{(2k) !}=1-\dfrac{1}{2}+\dfrac{1}{24}-\dfrac{1}{720}+\cdots\) converges.
Solution We begin by confirming that \(\lim\limits_{n\rightarrow \infty }a_{n}=\lim\limits_{n\rightarrow \infty }\dfrac{1}{(2n)!}=0\). Next using the Algebraic Ratio test, we verify that the terms \(a_{k}=\dfrac{1}{(2k) !}\) are nonincreasing. Since \[ \begin{eqnarray*} \dfrac{a_{n+1}}{a_{n}} &=& \dfrac{\dfrac{1}{[ 2(n+1) ] !} }{\dfrac{1}{(2n) !}}=\dfrac{(2n) !}{( 2n+2) !} =\dfrac{(2n) !}{( 2n+2) (2n+1) (2n) !}\\ &=&\dfrac{1}{( 2n+2) (2n+1) }<1 \qquad \hbox{for all }n\geq 1 \end{eqnarray*} \]
the terms \(a_{k}\) are nonincreasing. By the Alternating Series Test, the series converges.
NOW WORK
Problem 13.
2 Approximate the Sum of a Convergent Alternating Series
An important property of certain convergent alternating series is that we can estimate the error made by using a partial sum \(S_{n}\) to approximate the sum \(S\) of the series.
THEOREM Error Estimate for a Convergent Alternating Series
For a convergent alternating series \(\sum\limits_{k\,=\,1}^{\infty }(-1)^{k+1}\,a_{k}\) that satisfies the two conditions of the Alternating Series Test, the error \(E_{n}\) in using the sum \(S_{n}\) of the first \(n\) terms as an approximation to the sum \(S\) of the series is numerically less than or equal to the \((n+1)\)st term of the series. That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] {\left| {{E_n}} \right| \le {a_n} + 1}} \]
Proof
We follow the ideas used in the proof of the Alternating Series Test. If \(n\) is even, \(S_{n}<S\), and \[ 0<S-S_{n}=a_{n+1}-(a_{n+2}-a_{n+3})-\cdots \leq a_{n+1} \]
585
If \(n\) is odd, \(S_{n}>S\), and \[ 0<S_{n}-S=a_{n+1}-(a_{n+2}-a_{n+3})-\cdots \leq a_{n+1} \]
In either case, \[ \vert E_{n}\vert =\left\vert S-S_{n}\right\vert \leq a_{n+1} \]
In Example 1, we found that the alternating harmonic series converges. Table 4 shows how slowly the series converges. For example, using an additional \(900\) terms from \(99\) to \(999\) reduces the estimated error by only \(\vert E_{999}-E_{99}\vert =0.009\).
| Series | Number of Terms | Estimate of the Sum | Maximum Error |
|---|---|---|---|
| \[\sum\limits_{k = 1}^{^\infty } {\frac{{{{( - 1)}^{k + 1}}}}{k}} \] | \[n = 3\] | \[{S_3} = 1 - \frac{1}{2} + \frac{1}{3} \approx 0.833\] | \[\left| {{E_3}} \right| \le \frac{1}{4} = 0.25\] |
| \[n = 9\] | \[{S_9} = \sum\limits_{k = 1}^9 {\frac{{{{( - 1)}^{k + 1}}}}{k}} \approx 0.746\] | \[\left| {{E_9}} \right| \le \frac{1}{{10}} = 0.1\] | |
| \[n = 99\] | \[{S_{99}} = \sum\limits_{k = 1}^{99} {\frac{{{{( - 1)}^{k + 1}}}}{k}} \approx 0.7\] | \[\left| {{E_{99}}} \right| \le \frac{1}{{100}} = 0.01\] | |
| \[n = 999\] | \[{S_{999}} = \sum\limits_{k = 1}^{999} {\frac{{{{( - 1)}^{k + 1}}}}{k}} \approx 0.694\] | \[\left| {{E_{999}}} \right| \le \frac{1}{{1000}} = 0.001\] |
Approximating the Sum of a Convergent Alternating Series
Approximate the sum \(S\) of the alternating series correct to within 0.0001. \[ \sum\limits_{k = 0}^\infty {\frac{{{{( - 1)}^k}}}{{(2k)!}} = 1 - \frac{1}{{2!}} + \frac{1}{{4!}} - \frac{1}{{6!}} + \frac{1}{{8!}} - ...} \]
Solution We demonstrated in Example 2 that this series converges by showing that it satisfies the conditions of the Alternating Series Test. The fifth term of the series, \(\dfrac{1}{8!}=\dfrac{1}{40,\!320}\approx 0.000025\), is the first term less than or equal to \(0.0001\). This term represents an upper estimate to the error when the sum \(S\) of the series is approximated by adding the first four terms. So, the sum \[ S \approx \sum\limits_{k = 0}^3 {\frac{{{{( - 1)}^k}}}{{(2k)!}} = 1 - \frac{1}{{2!}} + \frac{1}{{4!}} - \frac{1}{{6!}} = 1 - \frac{1}{2} + \frac{1}{{24}} - \frac{1}{{720}} = \frac{{389}}{{720}} \approx 0.5403} \]
is correct to within 0.0001.
NOW WORK
Problem 19.
Absolute and Conditional Convergence
The ideas of absolute convergence and conditional convergence are used to describe the convergence or divergence of a series \(\sum\limits_{k=1}^{\infty }a_{k}\) in which the terms \(a_{k}\) are sometimes positive and sometimes negative (not necessarily alternating).
spanDEFINITIONspan Absolute Convergence
A series \(\sum\limits_{k=1}^{\infty }a_{k}\) is absolutely convergent if the series \[ \sum\limits_{k\,=\,1}^{\infty }\vert a_{k}\vert =\left\vert a_{1}\right\vert +\left\vert a_{2}\right\vert +\cdots +\vert a_{n}\vert +\cdots \]
is convergent.
586
THEOREM Absolute Convergence Test
If a series \(\sum\limits_{k=1}^{\infty }a_{k}\) is absolutely convergent, then it is convergent.
Proof
For any \(n\), \[ -\vert a_{n}\vert \leq a_{n}\leq \vert a_{n}\vert \]
Adding \(\vert a_{n}\vert\) yields \[ 0\leq a_{n}+\vert a_{n}\vert \leq 2\,\vert a_{n}\vert \]
Since \(\sum\limits_{k\,=\,1}^{\infty }\left\vert a_{k}\right\vert\) converges, then \(\sum\limits_{k\,=\,1}^{\infty }\,(2\vert a_{k}\vert) =2\sum\limits_{k\,=\,1}^{\infty }\vert a_{k}\vert\) also converges. By the Comparison Test for Convergence, \(\!\! \sum\limits_{k\,=\,1}^{\infty } ( a_{k}{+}\vert a_{k}\vert)\) converges. But \(a_{n}{=}( a_{n}{+}\vert a_{n}\vert) {-}\vert a_{n}\vert\). Since \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) is the difference of two convergent series, it also converges.
3 Determine Whether a Series Converges
Determine Whether a Series Converges
Determining whether a series \(1-\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}-\dfrac{1}{32}+\dfrac{1}{64}-\cdots\) converges.
Solution The series \(1 - \dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{8} -\dfrac{1}{16} - \dfrac{1}{32} + \dfrac{1}{64} - \cdots\) converges absolutely, since \(1 + \dfrac{1}{2} + \dfrac{1}{4} + \cdots + \dfrac{1}{2^{n-1}}+ \cdots = \sum\limits_{k\,=\,1}^{\infty }\left( \dfrac{1}{2}\right) ^{k-1}\), a geometric series with \(r=\dfrac{1}{2}\), converges. So by the Absolute Convergence Test, the series \(1-\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}-\dfrac{1}{32}+\dfrac{1}{64}-\cdots\) converges.
NOW WORK
Problem 31.
Determining Whether a Series Converges
Determine whether the series \(\sum\limits_{k=1}^{\infty }\dfrac{\sin k}{k^{2}}=\dfrac{\sin 1}{1^{2}}+\dfrac{\sin \,2}{2^{2}}+\dfrac{\sin 3}{3^{2}}+\cdots\) converges.
Solution This series has both positive and negative terms, but it is not an alternating series. Use the Absolute Convergence Test to investigate the series \(\sum\limits_{k=1}^{\infty }\left\vert \dfrac{\sin k}{k^{2}}\right\vert\). Since \[ \left\vert \frac{\sin n}{n^{2}}\right\vert \leq \frac{1}{n^{2}} \]
for all \(n\), and since \(\sum\limits_{k=1}^{\infty}\dfrac{1}{k^{2}}\) is a convergent \(p\)-series, then by the Comparison Test for Convergence, the series \(\sum\limits_{k=1}^{\infty }\left\vert \dfrac{\sin k}{k^{2}}\right\vert\) converges. Since \(\sum\limits_{k=1}^{\infty }\dfrac{\sin k}{k^{2}}\) is absolutely convergent, it follows that \(\sum\limits_{k=1}^{\infty }\dfrac{\sin k}{k^{2}}\) is convergent.
NOW WORK
Problem 29.
587
The converse of the Absolute Convergence Test is not true. That is, if a series is convergent, the series may or may not be absolutely convergent. There are convergent series that are not absolutely convergent. For instance, we have shown that the alternating harmonic series \[ \sum_{k=1}^{\infty }\frac{(-1)^{k+1}}{k}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots \]
converges. The series of absolute values is the harmonic series \(\sum\limits_{k=1}^{\infty }\dfrac{1}{k}\), which is divergent.
IN WORDS
If a series is absolutely convergent, then it is convergent. But just because a series converges does not mean it is absolutely convergent.
spanDEFINITIONspan Conditional Convergence
A series that is convergent without being absolutely convergent is called conditionally convergent.

Determining Whether a Series Is Absolutely or Conditionally Convergent or Divergent
Determine the numbers \(p\) for which the series \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{(-1)^{k+1}}{k^{p\,}}\) is absolutely convergent, conditionally convergent, or divergent.
Solution We begin by testing the series for absolute convergence. The series of absolute values is \(\sum\limits_{k\,=\,1}^{\infty}\left\vert \dfrac{(-1)^{k+1}}{k^{p\,}}\right\vert=\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k^{p\,}}\). This is a \(p\)-series, which converges if \(p>1\) and diverges if \(p\leq 1\). So, \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{(-1)^{k+1}}{k^{p\,}}\) is absolutely convergent if \(p>1\).
It remains to determine what happens when \(p\leq 1\). We use the Alternating Series Test, and begin by investigating \(\lim\limits_{n\,\rightarrow \infty }\,a_{n}\):
- \(\lim\limits_{n\,\rightarrow \infty }\dfrac{1}{n^{p}}=0\quad 0<p≤1\)
- \(\lim\limits_{n\,\rightarrow \infty }\dfrac{1}{n^{p}}=1\quad p=0\)
- \(\lim\limits_{n\,\rightarrow \infty }\dfrac{1}{n^{p}}= \infty \quad p<0\)
Consequently, \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{(-1)^{k+1}}{k^{p\,}}\) diverges if \(p\leq 0\).
Continuing, we check the second condition of the Alternating Series Test when \(0<p\leq 1.\) Using the related function \(f(x) =\dfrac{1}{x^{p}},\) for \(x>0,\) we have \(f^{\prime} (x) =-\dfrac{p}{x^{p+1}}\). Since \(f^{\prime} (x) <0\) for \(0<p\leq 1\), the second condition of the Alternating Series Test is satisfied. We conclude that \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{(-1)^{k+1}}{k^{p\,}}\) is conditionally convergent if \(0<p\leq 1\).
To summarize, the alternating \(p\)-series, \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{(-1)^{k+1}}{k^{p\,}}\) is absolutely convergent if \(p>1,\) conditionally convergent if \(0<p\leq 1,\) and divergent if \(p\leq 0.\)
NOW WORK
Problem 33.
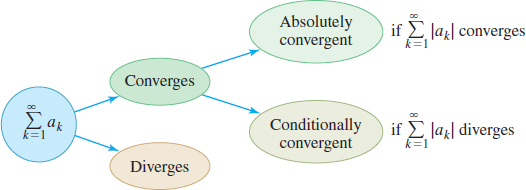
As illustrated in Figure 24, a series \(\sum\limits_{k\,=\,1}^{\infty}a_{k}\) is either convergent or divergent. If it is convergent, it is either absolutely convergent or conditionally convergent. The flowchart in Figure 25 can be used to determine whether a series is absolutely convergent, conditionally convergent, or divergent.
588

Absolute convergence of a series is stronger than conditional convergence, and absolutely convergent series and conditionally convergent series have different properties. We state, but do not prove, some of these properties now.
Properties of Absolutely Convergent and Conditionally Convergent Series
- If a series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) is absolutely convergent, any rearrangement of its terms results in a series that is also absolutely convergent. Both series will have the same sum. See Problem 66.
- If two series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) and \(\sum\limits_{k\,=\,1}^{\infty }b_{k}\) are absolutely convergent, the series \(\sum\limits_{k\,=\,1}^{\infty }(a_{k}+b_{k})\) is also absolutely convergent. Moreover, \[ \sum\limits_{k\,=\,1}^{\infty}\,(a_{k}+b_{k})=\sum\limits_{k\,=\,1}^{\infty}a_{k}+\sum\limits_{k\,=\,1}^{\infty }b_{k} \] See Problem 62.
- If two series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) and \(\sum\limits_{k\,=\,1}^{\infty }b_{k}\) are absolutely convergent, then the series \[ \sum\limits_{k\,=\,1}^{\infty }c_{k}=\sum\limits_{k\,=\,1}^{\infty}( a_{1}b_{k}+a_{2}b_{k -1} +\cdots +a_{k} b_1) \] is also absolutely convergent. The sum of the series \(\sum\limits_{k\,=\,1}^{\infty }c_{k}\) equals the product of the sums of the two original series.
- If a series converges absolutely, then the series consisting of just the positive terms converges, as does the series consisting of just the negative terms. See Problem 63.
- If a series converges conditionally, then the series consisting of just the positive terms diverges, as does the series consisting of just the negative terms. See Problems 51, 52, and 64.
- If a series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) is conditionally convergent, its terms may be rearranged to form a new series that converges to any sum we like. In fact, they may be rearranged to form a divergent series. See Problems 53–55.