OBJECTIVES

When you finish this section, you should be able to:

1. Approximate functions and their graphs (p. 623)
2. Approximate the number \(e;\) approximate logarithms (p. 625)
3. Approximate definite integrals (p. 627)

Approximating \(y=\sin x\)

1. Approximate \(y=\sin x\) by using the first four nonzero terms of its Maclaurin expansion.
2. Graph \(y=\sin x\) along with the approximation found in (a).
3. Use (a) to approximate \(\sin 0.1.\)
4. What is the error in using this approximation?

Solution (a) The Maclaurin expansion for \(y=\sin x\) was found in Example 3 (p. 616) of Section 8.9. \[ y=\sin x=x-\dfrac{x^{3}}{3!}+\dfrac{x^{5}}{5!}-\dfrac{x^{7}}{7!}+\cdots=\sum\limits_{k\,=\,0}^{\infty }\,(-1) ^{k}\dfrac{x^{2k+1} }{(2k+1) !} \]

Using the first four nonzero terms of the Maclaurin expansion, we can approximate \(\sin x\) as \[ \begin{equation*} \sin x\approx x-\dfrac{x^{3}}{3!}+\dfrac{x^{5}}{5!}-\dfrac{x^{7}}{7!} \tag{1} \end{equation*} \]

Figure 29

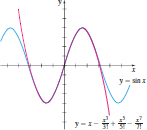
(b) The graphs of \(y=\sin x\) and the approximation in (1) are given in Figure 29.

(c) Using (1), we get \[ \sin 0.1\approx 0.1-\dfrac{0.1^{3}}{3!}+\dfrac{0.1^{5}}{5!}-\dfrac{0.1^{7}}{7!}\approx 0.0998 \]

(d) Since the Maclaurin expansion for \(y=\sin x\) at \(x=0\) is an alternating series that satisfies the conditions of the Alternating Series Test, the error \(E\) in using the first four terms as an approximation is less than or equal to the absolute value of the \(5\)th term at \(x=0.1.\) That is, \[ E\leq \left\vert \dfrac{0.1^{9}}{9!}\right\vert = 2.\, 756\times 10^{-15} \]

NOW WORK

Problem 1.

Approximating \(y=\sqrt{1+x}\)

1. Write the Maclaurin expansion for \(y=\sqrt{1+x}\) using a binomial series.
2. Approximate \(\sqrt{1+x}\) using the first five terms of the Maclaurin series.
3. Graph \(y=\sqrt{1+x}\) together with the first five terms of the approximation found in (b).
4. Comment on the graphs in (c).
5. Use the first five terms of the approximation for \(\sqrt{1+x}\) to approximate \(\sqrt{1.2}\). What is the error in using this approximation.

Solution (a) For \(-1\leq x\leq 1\), we have \begin{eqnarray}\quad \sqrt{1+x} &=&(1+x) ^{1/2}=\sum\limits_{k\,=\,0}^{\infty }{{ \dfrac{1}{2}}\choose {\vphantom{\vrule height10pt depth.2pt}k}}\,x^{k} \nonumber\\[8pt] &=& {1}+\dfrac{1}{2}{\,}x+\dfrac{\dfrac{1}{2}\left( - \dfrac{1}{2}\right) }{2!}x^{2}+\dfrac{\dfrac{1}{2}\,\left( -\dfrac{1}{2} \right) \left( -\dfrac{3}{2}\right) }{3!}\,x^{3}+\cdots +{{\dfrac{1}{2 }}\choose {\vphantom{\vrule height10pt depth.2pt}n}}x^{n}+\cdots \nonumber \end{eqnarray}

(b) From part (a), we have \[ \begin{equation*} \sqrt{1+x} \approx 1+\dfrac{1}{2}x-\dfrac{1}{8}x^{2}+\dfrac{1}{16}x^{3}-\dfrac{5}{128}x^{4} \tag{2} \end{equation*} \]

Figure 30

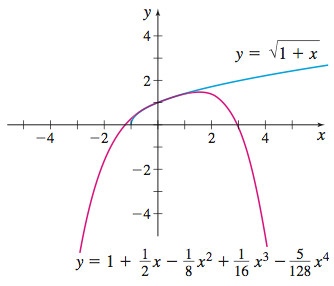
(c) The graphs of \(y=\sqrt{1+x}\) and the first five terms of the approximation in (2) are given in Figure 30.

(d) On the interval of convergence \([-1,1]\), the graphs are almost identical. Outside this interval, the graphs diverge.

(e) Using (2) and \(x=0.2,\) we have \[ \sqrt{1.2}\approx 1+\dfrac{1}{2}(0.2) -\dfrac{1}{8}(0.2) ^{2}+\dfrac{1}{16}(0.2) ^{3}-\dfrac{5}{128}(0.2) ^{4}=1.0954375 \]

Since the binomial series for \(y=\sqrt{1+x}\) at \(x=0.2\) is an alternating series that satisfies the conditions of the Alternating Series Test, the error \(E\) in using the first five terms of the series as an approximation of \(\sqrt{1.2}\) is less than or equal to the absolute value of the 6th term at \(x=0.2.\) That is, \[ \begin{eqnarray*} &&E\leq \left\vert \dfrac{\dfrac{1}{2}\,\left( -\dfrac{1}{2}\right) \left( -\dfrac{3}{2}\right) \left( -\dfrac{5}{2}\right) \left(- \dfrac{7}{2}\right)}{5!}\,x^{5}\right\vert \underset{\underset{\color{#0066A7}{\scriptsize\hbox{x=0.2}}}{\color{#0066A7}{\uparrow}}}{=} \dfrac{7}{256}(0.2) ^{5}= 8.\, 75\times 10^{-6}\\[-23pt] \end{eqnarray*} \]

NOW WORK

Problem 3.

Approximating \(e\)

Approximate \(e\) correct to within 0.000001.

Solution In Example 2 (p. 615) of Section 8.9, we showed that the Maclaurin series \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{x^{k}}{k!}\) converges to \(e^{x}\) for every number \(x.\) If \(x=1,\) we have \[ e=e^{1}=1+1+\dfrac{1}{2!}+\dfrac{1}{3!}+\cdots \,+\dfrac{1}{n!}+\cdots\, =\sum\limits_{k\,=\,0}^{\infty }\dfrac{1}{k!} \]

But this series converges very slowly.

For faster convergence, we can use \(x=-1.\) Then \[ e^{-1}=1-1+\dfrac{1}{2!}-\dfrac{1}{3!}+\cdots \,+\dfrac{(-1) ^{n}}{n!}+\cdots \,=\sum\limits_{k\,=\,0}^{\infty }\dfrac{(-1) ^{k}}{k!} \]

Since this series is an alternating series that satisfies the conditions of the Alternating Series Test, we can use the error estimate for an alternating series. Since we want \(e\) correct to within 0.000001, we need the error \(E<0.000001.\) That is, we need \(\dfrac{1}{n!}<0.000001,\) or equivalently, \(n!>10^{6}\). Since \(10!= 3.6288\times 10^{6}>10^{6},\) but \(9!= 362{,}880<10^{6},\) using \(10\) terms of the Maclaurin series will approximate \(e^{-1}\) correct to within 0.000001.

\[ \sum\limits_{k\,=\,0}^{9}\dfrac{(-1) ^{k}}{k!}=1-1+\dfrac{1}{2}- \dfrac{1}{3!}+\dfrac{1}{4!}-\dfrac{1}{5!}+\dfrac{1}{6!}-\dfrac{1}{7!}+\dfrac{ 1}{8!}-\dfrac{1}{9!}=\dfrac{16{,}687}{45{,}360} \]

Then \[ e=\dfrac{1}{e^{-1}}= \left( \dfrac{16{,}687}{45{,}360}\right)^{-1}\approx 2.\, 718\,28 \]

correct to within 0.000001.

NOW WORK

Problem 19.

Approximating a Logarithm

1. Approximate \(\ln 2\) using the first three terms of (7).
2. Approximate \(\ln 3\) using the first three terms of (7).

Solution (a) In (7), we let \(N=1\) and use the first three terms of the series; then \[ \ln 2\approx 2 \, \left[ \frac{1}{3}+\frac{1}{3}\left( \frac{1}{3}\right) ^{3}+\frac{1}{5}\left( \frac{1}{3}\right) ^{5} \right] \approx 0.693004 \]

(The first three terms of this series approximates \(\ln 2\) correct to within 0.001.)

(b) To find \(\ln 3\), let \(N=2\) and use \(\ln 2=0.693004\) in (7). \begin{eqnarray*} \ln 3 & \approx & \ln 2+2 \,\left[ \dfrac{1}{5}+\dfrac{1}{3}\left( \dfrac{1}{5} \right) ^{3}+\dfrac{1}{5}\left( \dfrac{1}{5}\right) ^{5}\right] \\ & \approx & 0.693004+2\left[ \dfrac{1}{5}+\dfrac{1}{3}\left( \dfrac{1}{5}\right) ^{3}+ \dfrac{1}{5}\left( \dfrac{1}{5}\right) ^{5}\right] \approx 1.098465 \end{eqnarray*}

NOW WORK

Problem 15.

Using a Maclaurin Expansion to Approximate an Integral

Use a Maclaurin expansion to approximate \(\int_{0}^{1/2}e^{-x^{2}}dx\) correct to within 0.001.

Solution Replace \(x\) by \(-x^{2}\) in the Maclaurin expansion for \(e^{x}\) to obtain the Maclaurin expansion for \(e^{-x^{2}}\). \[ \begin{eqnarray*} e^{x} &=& 1+x+\dfrac{x^{2}}{2!}+\dfrac{x^{3}}{3!}+\,...\, \\[7pt] e^{-x^{2}} &=& 1-x^{2}+\frac{x^{4}}{2!}-\frac{x^{6}}{3!}+\frac{x^{8}}{4!}-\cdots \end{eqnarray*} \]

Now use the integration property of power series. \[ \begin{eqnarray*} \int_{0}^{1/2}e^{-x^{2}}dx &=& \int_{0}^{1/2}\left( 1-x^{2}+\frac{x^{4}}{2!}-\frac{x^{6}}{3!}+\cdots \right)\,dx \\[9pt] &=& \left[ x-\frac{x^{3}}{3}+\frac{x^{5}}{2!5}-\frac{x^{7}}{3!7}+\cdots \right] _{0}^{1/2} \\[9pt] &=& \frac{1}{2}-\frac{1}{3(2)^{3}}+\frac{1}{2!5(2)^{5}}-\frac{1}{3!7(2)^{7}}+\cdots \\[9pt] &\approx & 0.5-0.041666+0.003125-0.000186+\cdots \end{eqnarray*} \]

Since this series satisfies the two conditions of the Alternating Series Test, the error due to using the first three terms as an approximation is less than the 4th term,

\(\dfrac{1}{3!7(2)^{7}}= 1.\, 860119048\times 10^{-4}. \) So, \[ \int_{0}^{1/2}e^{-x^{2}}dx\approx \frac{1}{2}-\frac{1}{3(2)^{3}}+\frac{1}{2!5(2)^{5}}\approx 0.461458 \]

correct to within \(0.001\).

NOW WORK

Problem 9.