8.1 Assess Your UnderstandingPrinted Page 550
Concepts and Vocabulary
True or False A sequence is a function whose domain is the set of positive real numbers.
False
True or False If the sequence {sn} is convergent, then lim
False
True or False If f(x) is a related function of the sequence \{ s_{n}\} and there is a real number L for which \lim\limits_{x\,\rightarrow \,\infty }\,f(x) =L, then \{ s_{n}\} converges.
True
Multiple Choice If there is a positive number K for which \vert s_{n}\vert \leq K for all integers n\geq 1, then \{ s_{n}\} is [(a) increasing, (b) bounded, (c) decreasing, (d) convergent.]
(b)
True or False A bounded sequence is convergent.
False
True or False An unbounded sequence is divergent.
True
True or False A sequence \{ s_{n}\} is decreasing if and only if s_{n}\leq s_{n+1} for all integers n\geq 1.
False
True or False A sequence must be monotonic to be convergent.
False
True or False To use an algebraic ratio to show that the sequence \{ s_{n}\} is increasing, show that \dfrac{s_{n+1}}{s_{n}}\geq 0 for all n\geq 1.
False
Multiple Choice If the derivative of a related function f of a sequence \{ s_{n}\} is negative, then the sequence \{ s_{n}\} is [(a) bounded, (b) decreasing, (c) increasing, (d) convergent.]
(b)
True or False When determining whether a sequence \{ s_{n}\} converges or diverges, the beginning terms of the sequence can be ignored.
True
True or False Sequences that are both bounded and monotonic diverge.
False
Skill Building
In Problems 13–22, the nth term of a sequence \{ s_{n}\} is given. Write the first four terms of each sequence.
s_{n}=\dfrac{n+1}{n}
2, \dfrac{3}{2}, \dfrac{4}{3}, \dfrac{5}{4}
s_{n}=\dfrac{2}{n^{2}}
s_{n}=\ln n
0, \ln2, \ln3, \ln4
s_{n}=\dfrac{n}{\ln (n+1)}
s_{n}=\dfrac{(-1)^{n+1}}{2n+1}
\dfrac{1}{3}, -\dfrac{1}{5}, \dfrac{1}{7}, -\dfrac{1}{9}
s_{n}=\dfrac{1-(-1)^{n}}{2}
s_{n}=\left\{ \begin{array}{@{}l@{\quad}ll} (-1)^{n+1} & \hbox{if} & n~\hbox{is even} \\ 1 & \text{if} & n\hbox{ is odd} \end{array} \right.
1, -1, 1, -1
s_{n}=\left\{ \begin{array}{@{}l@{\quad}ll} n^{2}+n & \text{if} & ~n~\hbox{is even} \\ 4n+1 & \text{if} & ~n~\hbox{is odd} \end{array} \right.
s_{n}=\dfrac{n!}{2^{n}}
\dfrac{1}{2}, \dfrac{1}{2}, \dfrac{3}{4}, \dfrac{3}{2}
s_{n}=\dfrac{n!}{n^{2}}
In Problems 23–32, the first few terms of a sequence are given. Find an expression for the nth term of each sequence, assuming the indicated pattern continues for all n.
2, 4, 6, 8, 10, \ldots
a_n=2n
1, 3, 5, 7, 9, \ldots
2,~4,~8,~16,~32, \ldots
a_n=2^n
1, 8, 27, 64, 125, \ldots
\dfrac{1}{2}, -\dfrac{1}{3}, \dfrac{1}{4}, -\dfrac{1}{5}, \dfrac{1}{6}, \ldots
a_n=\dfrac{(-1)^{n+1}}{n+1}
1, -2, 3, -4, 5, \ldots
\dfrac{1}{2}, \dfrac{2}{3},~\dfrac{3}{4},~\dfrac{4}{5}, \ldots
a_n=\dfrac{n}{n+1}
\dfrac{1}{2}, \dfrac{4}{3},~\dfrac{9}{4},~\dfrac{16}{5},\ldots
1,1,2,6,24,120,720, \ldots
a_n=(n-1)!
1,1,\dfrac{1}{2},\dfrac{1}{6},\dfrac{1}{24},\dfrac{1}{120},\ldots
In Problems 33–44, use properties of convergent sequences to find the limit of each sequence.
\left\{\dfrac{3}{n}\right\}
0
\left\{\dfrac{-2}{n}\right\}
\left\{1-\dfrac{1}{n}\right\}
1
\left\{\dfrac{1}{n}+4\right\}
\left\{\dfrac{4n+2}{n}\right\}
4
\left\{ {\dfrac{2n+1}{n}}\right\}
\left\{ \left( \dfrac{2-n}{n^{2}}\right) ^{4}\right\}
0
\left\{ \left( \dfrac{n^{3}-2n}{n^{3}}\right) ^{2}\right\}
\left\{ \sqrt{\dfrac{n+1}{n^{2}}}\right\}
0
\left\{ \sqrt[3]{8-\dfrac{1}{n}}\right\}
\left\{ {\left( {1-\dfrac{1^{~}}{n}}\right) \left( {1-\dfrac{1^{~}}{n^{2}}}\right) }\right\}
1
551
\left\{ {\left( {1-\dfrac{1^{~}}{n}}\right) \left( {1-\dfrac{1^{~}}{n^{2}}}\right) \left( {1-\dfrac{1^{~}}{n^{3}}}\right) }\right\}
In Problems 45–50, show that each sequence converges. Find its limit.
\left\{ \ln {\dfrac{n+1^{~}}{3n}}\right\}
\ln\dfrac{1}{3}
\left\{\ln \dfrac{n^{2}+2}{2n^{2}+3}\right\}
\left\{e^{(4/n) -2}\right\}
e^{-2}
\left\{e^{3+(6/n) }\right\}
\left\{\sin \dfrac{1}{n}\right\}
0
\left\{\cos \dfrac{1}{n}\right\}
In Problems 51–62, use a related function or the Squeeze Theorem for sequences to show each sequence converges. Find its limit.
\left\{ \dfrac{n^{2}-4}{n^{2}+n-2}\right\}
1
\left\{ \dfrac{n+2}{n^{2}+6n+8}\right\}
\left\{ {\dfrac{n^{2}}{2n+1}-\dfrac{n^{2}}{2n-1}}\right\}
-\dfrac{1}{2}
\left\{ {\dfrac{6n^{4}-5}{7n^{4}+3}}\right\}
\left\{ {\dfrac{\sqrt{n}+2}{\sqrt{n}+5}}\right\}
1
\left\{ {\dfrac{\sqrt{n}}{e^{n}}}\right\}
\left\{ {\dfrac{n^{2}}{3^{n}}}\right\}
0
\left\{\dfrac{(n-1)^{2}}{e^{n}}\right\}
\left\{ \dfrac{(-1) ^{n}}{3n^{2}}\right\}
0
\left\{ \dfrac{(-1) ^{n}}{\sqrt{n}}\right\}
\left\{ \dfrac{\sin n}{n}\right\}
0
\left\{ \dfrac{\cos n}{n}\right\}
In Problems 63–72, determine whether each sequence converges or diverges.
\left\{\cos \left( \pi n\right) \right\}
Diverges
\left\{ \cos \left( \dfrac{\pi }{2}n\right) \right\}
\left\{ \sqrt{n}\right\}
Diverges
\left\{ n^{2}\right\}
\left\{ \left(-\dfrac{1}{3}\right) ^{n}\right\}
Converges
\left\{ \left( {\dfrac{1}{3}}\right) ^{n}\right\}
\left\{ \left( \dfrac{5}{4}\right)^{n}\right\}
Diverges
\left\{ \left( \dfrac{\pi }{2}\right) ^{n}\right\}
\left\{ {\dfrac{n+(-1)^{n}}{n}}\right\}
Converges
\left\{ \dfrac{1}{n}+(-1)^{n}\right\}
In Problems 73–80, determine whether each sequence is bounded from above, bounded from below, both, or neither.
\left\{ \dfrac{\ln n}{n}\right\}
Bounded from above and from below
\left\{\dfrac{\sin n}{n}\right\}
\left\{n+\dfrac{1}{n}\right\}
Bounded from below
\left\{\dfrac{3}{n+1}\right\}
\left\{ \dfrac{n^{2}}{n+1}\right\}
Bounded from below
\left\{ \dfrac{2^{n}}{n^{2}}\right\}
\left\{ \left( -\dfrac{1}{2}\right) ^{n}\right\}
Bounded from above and from below
\left\{ n^{1/2}\right\}
In Problems 81–88, determine whether each sequence is monotonic. If the sequence is monotonic, is it increasing, nondecreasing, decreasing, or nonincreasing?
\left\{ \dfrac{3^{n}}{(n+1) ^{3}}\right\}
Nonmonotonic
\left\{ {\dfrac{2n+1}{n}}\right\}
\left\{ \dfrac{\ln n}{\sqrt{n}}\right\}
Nonmonotonic
\left\{ {\dfrac{\sqrt{n+1}}{n}}\right\}
\left\{ {\left( {\dfrac{1}{3}}\right) ^{n}}\right\}
Monotonic decreasing
\left\{ \dfrac{n^{2}}{5^{n}}\right\}
\left\{ {\dfrac{n!}{3^{n}}}\right\}
Nonmonotonic
\left\{ {\dfrac{n!}{n^{2}}}\right\}
In Problems 89–94, show that each sequence converges by showing it is either increasing (nondecreasing) and bounded from above or decreasing (nonincreasing) and bounded from below.
\left\{ ne^{-n}\right\}
Decreasing, bounded from below
\left\{\tan ^{-1}n\right\}
\left\{\dfrac{n}{n+1}\right\}
Increasing, bounded from above
\left\{\dfrac{n}{n^{2}+1}\right\}
\left\{2-\dfrac{1}{n}\right\}
Increasing, bounded from above
\left\{\dfrac{n}{2^{n}}\right\}
In Problems 95–114, determine whether each sequence converges or diverges. If it converges, find its limit.
\left\{ {\dfrac{3}{n}+6}\right\}
Converges; 6
\left\{ {2-\dfrac{4}{n}}\right\}
\left\{ \ln \left({\dfrac{n+1^{~}}{3n}}\right) \right\}
Converges; -\ln3
\left\{\cos\left( {{n\pi +\dfrac{\pi }{2}}}\right) \right\}
\left\{ (-1)^{n}\sqrt{n}\right\}
Diverges
\left\{ {\dfrac{(-1)^{n}}{2n}}\right\}
\left\{ \dfrac{3^{n}+1}{4^{n}}\right\}
Converges; 0
\left\{ {n+\sin \dfrac{1}{n}}\right\}
\left\{ {\dfrac{\ln (n+1)}{n+1}}\right\}
Converges; 0
\left\{ \dfrac{\ln (n+1)}{\sqrt{n}}\right\}
\kern1.7pt\{0.5^{n}\}
Converges; 0
\left\{(-2) ^{n}\right\}
\left\{\cos \dfrac{\pi}{n}\right\}
Converges; 1
\left\{\sin \dfrac{\pi}{n}\right\}
\left\{\cos \left( \dfrac{n}{e^{n}}\right) \right\}
Converges; 1
\left\{\sin \left( \dfrac{(n+1)^{3}}{e^{n}}\right) \right\}
\left\{e^{1/n}\right\}
Converges; 1
\left\{ {\dfrac{1}{ne^{-n}}}\right\}
\left\{ 1+\left( \dfrac{1}{2}\right)^{n}\right\}
Converges; 1
\left\{ 1-\left( \dfrac{1}{2}\right) ^{n}\right\}
Applications and Extensions
In Problems 115–124, determine whether each sequence converges or diverges.
\left\{ {\dfrac{n^{2}\tan ^{-1}n}{n^{2}+1}}\right\}
Converges
\left\{ n\sin \dfrac{1}{n}\right\}
\left\{ {\dfrac{n+\sin n}{n+\cos (4n) }}\right\}
Converges
\left\{ {\dfrac{n^{2}}{2n+1}\sin \dfrac{1}{n}}\right\}
\{\ln n-\ln (n+1)\}
Converges
\left\{ \ln n^{2}+\ln \dfrac{1}{n^{2}+1}\right\}
\left\{ {\dfrac{n^{2}}{\sqrt{n^{2}+1}}}\right\}
Diverges
\left\{\dfrac{5^{n}}{(n+1)^{2}}\right\}
\left\{ \dfrac{2^{n}}{(2)(4)(6)\cdots (2n)}\right\}
Converges
\left\{ \dfrac{3^{n+1}}{(3)(6)(9)\cdots (3n)}\right\}
The nth term of a sequence is s_{n}=\dfrac{1}{n^{2}+n\cos n+1}. Does the sequence \{ s_{n}\} converge or diverge? (Hint: Show that the derivative of \dfrac{1}{x^{2}+x\cos x+1} is negative for x>1.)
Converges
552
Fibonacci Sequence The famous Fibonacci sequence \left\{ u_{n}\right\} is defined recursively as u_{1}=1 \qquad u_{2}=1 \qquad u_{n+2}=u_{n}+u_{n+1} \quad n\geq 1
- (a) Write the first eight terms of the Fibonacci sequence.
- (b) Verify that the nth term is given by u_{n}=\frac{(1+\sqrt{5})^{n}-(1-\sqrt{5})^{n}}{2^{n}\sqrt{5}} (Hint: Show that u_{1}=1,~u_{2}=1, and u_{n+2}=u_{n+1}+u_{n}.)
Stocking a Lake Mirror Lake is stocked with rainbow trout. Considering fish reproduction and natural death, along with vigorous efforts by fishermen to decimate the population, managers find that some ratio r, 0<r<1, of the population persists from one stocking period to the next. If the lake is stocked with h fish each year, the fish population p_{n}, in year n of the stocking program, is approximately p_{n}=rp_{n-1}+h. If p_{0} is 3000, write a general expression for the nth term of the sequence in terms of r and h only. Does this sequence converge?
p_n=3000r^n+h\dfrac{r^n-1}{r-1} Converges \lim\limits_{n\to\infty}p_n=\dfrac{h}{1-r}
Electronics: A Discharging Capacitor A capacitor is an electronic device that stores an electrical charge. When connected across a resistor, it loses the charge (discharges) in such a way that during a fixed time interval, called the time constant, the charge stored in the capacitor is \dfrac{1}{e} of the charge at the beginning of that interval.
- (a) Develop a sequence for the charge remaining after n time constants if the initial charge is Q_{0}.
- (b) Does this sequence converge? If yes, to what?
Reflections in a Mirror A highly reflective mirror reflects 95\% of the light that falls on it. In a light box having walls made of this mirror, the light will reflect back-and-forth between the mirrors.
- (a) If the original intensity of the light is I_{0} before it falls on a mirror, develop a sequence to describe the intensity of the light after n reflections.
- (b) How many reflections are needed to reduce the light intensity by at least 98\%?
- (a) I_n=0.95^nI_0
- (b) 77
A Fission Chain Reaction A chain reaction is any sequence of events for which each event causes one or more additional events to occur. For example, in chain-reaction auto accidents, one car rear-ends another car, that car rear-ends another, and so on. In one type of nuclear fission chain reaction, a uranium-235 nucleus is struck by a neutron, causing it to break apart and release several more neutrons. Each of these neutrons strikes another nucleus, causing it to break apart and release additional neutrons, resulting in a chain reaction. In the fission of uranium-235 in nuclear reactors, each fission event releases an average of 2\dfrac{1}{2} neutrons, and each of these neutrons causes another fission event. The first fission is triggered by a single free neutron.
- (a) Develop a sequence for the average number of neutrons, that is, fission events, that occur at the nth event if we start with one such event.
- (b) Does the sequence converge or diverge?
- (c) Interpret the answer found in (b).
Challenge Problems
- (a) Show that the sequence \{ e^{n/(n+2)}\} converges.
- (b) Find \lim\limits_{n\rightarrow \infty }e^{n/(n+2) }.
- (c)
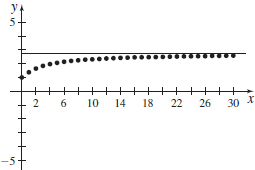
 Graph y=e^{n/(n+2) }. Does the graph confirm the results of (a) and (b)?
Graph y=e^{n/(n+2) }. Does the graph confirm the results of (a) and (b)?
- (a) See Student Solutions Manual.
- (b) \lim\limits_{n\to\infty}e^{n/(n+2)}=e
- (c)
Show that if 0<r<1, then \lim\limits_{n\,\rightarrow \,\infty }\,r^{n}=0. Hint: Let r=\dfrac{1}{1+p}, where p>0. Then, by the Binomial Theorem, r^{n}=\dfrac{1}{(1+p)^{n}}= \dfrac{1}{1+np+n(n-1)\dfrac{p^{2}}{2}+\cdots +p^{n}}<\dfrac{1}{np}.
Use the result of Problem 132 to show that if -1<r<0, then \lim\limits_{n\,\rightarrow \,\infty }\,r^{n}=0.
See Student Solutions Manual.
Show that if r>1, then \lim\limits_{n\rightarrow \,\infty }\,r^{n}=\infty. [Hint: Let r=1+p, where p>0. Then by the Binomial Theorem, r^{n}=(1+p)^{n}=1+np+n(n-1)\dfrac{p^{2}}{2}+\cdots+p^{n}>np.]
Use the result of Problem 134 to show that if r<-1, then \lim\limits_{n\,\rightarrow \,\infty }\,r^{n} does not exist. (Hint: r^{n} oscillates between positive and negative values.)
See Student Solutions Manual.
Suppose \{ s_{n}\} is a sequence of real numbers. Show that if \lim\limits_{n\rightarrow \infty }s_{n}=L and if f is a function that is continuous at L and is defined for all numbers s_{n}, then \lim\limits_{n\rightarrow \infty }f( s_{n})=f(L) .
Show that if \lim\limits_{n\,\rightarrow \,\infty}\,s_{n}=L, then \lim\limits_{n\rightarrow \,\infty }\,\vert s_{n}\vert exists and \lim\limits_{n\,\rightarrow \,\infty }\,\vert s_{n}\vert =\left\vert L\right\vert. Is the converse true?
See Student Solutions Manual.
The Limit of a Sequence Is Unique Show that a convergent sequence \{ s_{n}\} cannot have two distinct limits.
Review the definition of the limit at infinity of a function from Section 1.6. Write a paragraph that compares and contrasts the limit at infinity of a function f and the limit of a sequence \{ s_{n}\}.
Answers will vary.
- (a) Show that the sequence \{ \ln n\} is increasing.
- (b) Show that the sequence \{ \ln n\} is unbounded from above.
- (c) Conclude \{ \ln n\} diverges.
- (d)
 Find the smallest number N so that \ln N>20.
Find the smallest number N so that \ln N>20. - (e)
 Graph y=\ln x and zoom in for x large.
Graph y=\ln x and zoom in for x large. - (f) Does the graph confirm the result in (c)?
Let a_{1}> 0 and b_{1}>0 be two real numbers for which a_{1}>b_{1}. Define sequences \{a_{n}\} and \{b_{n}\} as a_{n+1}=\frac{a_{n}+b_{n}}{2}, \qquad b_{n+1}=\sqrt{a_{n}b_{n}}
- (a) Show that b_{n}<b_{n+1}<a_{1} for all n.
- (b) Show that b_{1}<a_{n+1}<a_{n} for all n.
553
- (c) Show that 0<a_{n+1}-b_{n+1}<\dfrac{a_{1}-b_{1}}{2^{n}}.
- (d) Show that \lim\limits_{n\,\rightarrow \,\infty }a_{n} and \lim\limits_{n\,\rightarrow \,\infty }\,b_{n} each exist and are equal.
See Student Solutions Manual.
In Problems 142–144, determine whether each sequence converges or diverges.
s_{n}=\dfrac{2^{n-1}\cdot 4^{n}}{n!}
s_{n}=\dfrac{n!}{3^{n}\cdot 4^{n}}
Diverges
s_{n}=\dfrac{n!}{3^{n}+8n}
Show that \left\{( 3^{n}+5^{n}) ^{1/n}\right\} converges.
See Student Solutions Manual.
Let N be a fixed positive number and define a sequence by \{a_{n+1}\} =\left\{ \dfrac{1}{2}\left[ a_{n}+\dfrac{N}{a_{n}}\right] \right\}, where a_{1} is a positive number.
- (a) Show that the sequence \{a_{n}\} converges to \sqrt{N}.
- (b) Use this sequence to approximate \sqrt{28} rounded to three decimal places. How accurate is a_{3}? a_{6}?
Show that \{ s_{n}\} =\left\{ \dfrac{1\cdot3\cdot 5\cdot \cdots \cdot \left( 2n-1\right) }{2\cdot 4\cdot 6\cdot \cdots\cdot 2n}\right\} is bounded and monotonic.
See Student Solutions Manual.
Show that \{ s_{n}\} =\left\{ \left( 1+\dfrac{1}{n}\right) ^{n}\right\} is increasing and bounded from above. Hint: Use the Binomial Theorem to expand \left( 1+\dfrac{1}{n}\right) ^{n}.
Let \{ s_{n}\} be a convergent sequence, and suppose the nth term of the sequence \{a_{n}\} is the arithmetic mean (average) of the first n terms of \{ s_{n}\}. That is, a_{n}=\dfrac{1}{n}\left[ s_{1}+s_{2}+\cdots +s_{n}\right] . Show that \{a_{n}\} converges and has the same limit as \{ s_{n}\}.
See Student Solutions Manual.
Area Let A_{n} be the area enclosed by a regular n-sided polygon inscribed in a circle of radius R. Show that:
- (a) A_{n}=\dfrac{n}{2}R^{2}\sin\! \left( \dfrac{2\pi }{n}\right).
- (b) \lim\limits_{n\rightarrow \infty}A_{n}=\lim\limits_{n\rightarrow \infty }\left[ \dfrac{n}{2}R^{2}\sin\! \left( \dfrac{2\pi }{n}\right) \right] =\pi R^{2} (the area of a circle of radius R).
Area Let A_{n} be the area enclosed by a regular n-sided polygon circumscribed around a circle of radius r. Show that:
- (a) A_{n}=nr^{2}\tan\! \left( \dfrac{\pi }{n}\right).
- (b) \lim\limits_{n\rightarrow \infty }A_{n}=\pi r^{2} (the area of a circle of radius r). (Hint: r, called the apothem of the polygon, is the perpendicular distance from the center of the polygon to the midpoint of a side.)
See Student Solutions Manual.
Perimeter Suppose P_{n} is the perimeter of a regular n-sided polygon inscribed in a circle of radius R. Show that:
- (a) P_{n}=2nR\sin \!\left( \dfrac{\pi }{n}\right).
- (b) {\lim\limits_{n\rightarrow \infty }P_{n}=2\pi R} (the circumference of a circle of radius R).
Cauchy Sequence A sequence \{ s_{n}\} is said to be a Cauchy sequence if and only if for each \varepsilon >0, there exists a positive integer N for which \left\vert s_{n}-s_{m}\right\vert < \varepsilon\qquad \hbox{ for all }n, m>N
Show that every convergent sequence is a Cauchy sequence.
See Student Solutions Manual.
