9.6 Assess Your UnderstandingPrinted Page 683
683
Concepts and Vocabulary
The area A of the sector of a circle of radius r and central angle θ is A= ______________.
θr22
True or False The area enclosed by the graph of a polar equation and two rays that have the pole as a common vertex is found by approximating the area using sectors of a circle.
True
True or False The area A enclosed by the graph of the equation r=f(θ), r≥0, and the rays θ=α and θ=β, is given by A=∫βαf(θ)dθ.
False
True or False If x(θ)=rcosθ, y(θ)=rsinθ are parametric equations of the polar equation r=f(θ), then (dxdθ)2+(dydθ)2=r2+(drdθ)2.
True
Skill Building
In Problems 5–8, find the area of the shaded region.
r=cos(2θ)
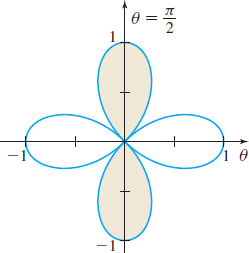
π4
r=2sin(3θ)

r=2+2sinθ
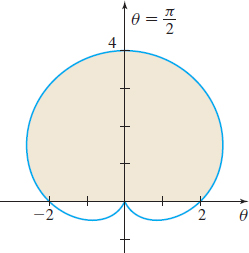
8+3π
r=3−3cosθ
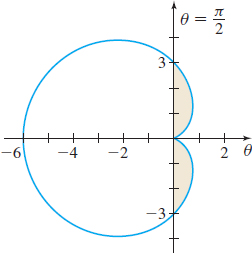
In Problems 9–12, find the area of the region enclosed by the graph of each polar equation swept out by the given rays.
r=3cosθ;θ=0toθ=π3
316(3√3+4π)
r=3sinθ;θ=0toθ=π4
r=aθ;θ=0 to θ=2π
4π3a23
r=eaθ;θ=0 to θ=π2
In Problems 13–18, find the area of the region enclosed by the graph of each polar equation.
r=1+cosθ
3π2
r=2−2sinθ
r=3+sinθ
19π2
r=3(2−sinθ)
r=8sin(3θ)
16π
r=cos(4θ)
In Problems 19–22, find the area of the region enclosed by one loop of the graph of each polar equation.
r=4sin(2θ)
2π
r=5cos(3θ)
r2=4cos(2θ)
2
r=a2cos(2θ)
In Problems 23–26, find the area of each region described.
Inside r=2sinθ; outside r=1
√32+π3
Inside r=4cosθ; outside r=2
Inside r=sinθ; outside r=1−cosθ
1−π4
Inside r2=4cos(2θ); outside r=√2
In Problems 27–30, find the surface area of the solid of revolution generated by revolving each curve about the polar axis.
r=sinθ,0≤θ≤π2
π22
r=1+cosθ,0≤θ≤π
r=eθ,0≤θ≤π
25√2(1+e2π)π
r=2acosθ,0≤θ≤π2
Applications and Extensions
In Problems 31–48, find the area of the region:
enclosed by the small loop of the limaçon r=1+2cosθ.
π−3√32
enclosed by the small loop of the limaçon r=1+2sinθ.
684
enclosed by the loop of the graph of r=2−secθ.
√3+4π3−4ln(2+√3)
enclosed by the loop of the graph of r=5+secθ.
enclosed by r=2sin2θ2.
3π2
enclosed by r=6cos2θ.
inside the circle r=8cosθ and to the right of the line r=2secθ.
4√3+32π3
inside the circle r=10sinθ and above the line r=2cscθ.
outside the circle r=3 and inside the cardioid r=2+2cosθ.
9√32−π
inside the circle r=sinθ and outside the cardioid r=1+cosθ.
common to the circle r=cosθ and the cardioid r=1−cosθ.
7π12−√3
common to the circles r=cosθ and r=sinθ.
common to the inside of the cardioid r=1+sinθ and the outside of the cardioid r=1+cosθ.
2√2
common to the inside of the lemniscate r2=8cos(2θ) and the outside of the circle r=2.
enclosed by the rays θ=0 and θ=1 and r=e−θ, 0≤θ≤1.
1−e−24
enclosed by the rays θ=0 and θ=1 and r=eθ, 0≤θ≤1.
enclosed by the rays θ=1 and θ=π and r=1θ, 1≤θ≤π.
π−12π
inside the outer loop but outside the inner loop of r=1+2sinθ.
Area Find the area of the loop of the graph of r=secθ+2.
√3+4π3−4 ln(2+√3)
Surface Area of a Sphere Develop a formula for the surface area of a sphere of radius R.
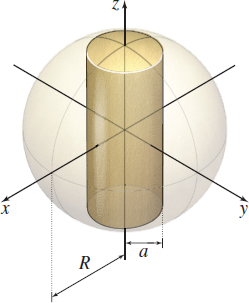
Surface Area of a Bead A sphere of radius R has a hole of radius a<R drilled through it. See the figure. The axis of the hole coincides with a diameter of the sphere.
- (a) Find the surface area of that part of the sphere that remains.
- (b) Is the area found in Problem 29, Section 9.3, the same as the area found here? If not, justify the difference.
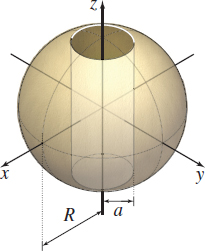
- (a) 4πR√R2−a2
- (b) Answers will vary
Surface Area of a Plug A plug is made to repair the hole in the sphere in Problem 51.
- (a) What is the surface area of the plug?
- (b) Is the area found in Problem 30, Section 9.3, the same as the area found here? If not justify the difference.
Area Find the area enclosed by the loop of the strophoid r=secθ−2cosθ,−π2<θ<π2 as shown in the figure.
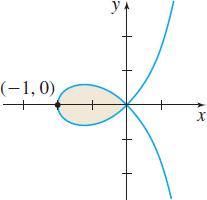
2−π2
 Area
Area- (a) Graph the limaçon r=2−3cosθ.
- (b) Find the area enclosed by the inner loop. Round the answer to three decimal places.
Challenge Problems
Show that the area enclosed by the graph of rθ=a and the rays θ=θ1 and θ=θ2 is proportional to the difference of the radii, r1−r2, where r1=aθ1 and r2=aθ2.
See Student Solutions Manual.
Find the area of the region that lies outside the circle r=1 and inside the rose r=3sin(3θ).
Find the area of the region that lies inside the circle r=2 and outside the rose r=3sin(2θ).
2√5−sin−1(23)
