9.7 Assess Your UnderstandingPrinted Page 688
Concepts and Vocabulary
Multiple Choice A(n) [(a) parabola, (b) ellipse, (c) hyperbola] is the set of points P in the plane for which the distance from a fixed point called the focus to P equals the distance from a fixed line called the directrix to P.
(a)
In your own words, explain what is meant by the eccentricity e of a conic.
Answers will vary.
Identify the graphs of each of these polar equations: r=21+sinθ and r=21+cosθ. How are they the same? How are they different?
Answers will vary.
True or False The polar equation of a conic with focus at the pole and directrix perpendicular to the polar axis at a distance p to the left of the pole is r=ep1−pcosθ, where e is the eccentricity of the conic.
False
Skill Building
In Problems 5–12, identify each conic. Find its eccentricity e and the position of its directrix.
r=11+cosθ
A parabola, e=1, directrix perpendicular to the polar axis p=1 units to the right of the pole
r=31−sinθ
r=42−3sinθ
A hyperbola, e=32, directrix parallel to the polar axis p=43 units below the pole
r=21+2cosθ
r=34−2cosθ
An ellipse, e=12, directrix perpendicular to the polar axis p=32 units to the left of the pole
r=68+2cosθ
r=43+3sinθ
A parabola, e=1, directrix parallel to the polar axis p=43 units above the pole
r=16+2sinθ
In Problems 13–20, for each polar equation:
(a) Identify and graph the equation.
(b) Convert the polar equation to a rectangular equation.
(c) Find parametric equations for the polar equation.
689
r=84+3sinθ
- (a) Ellipse

- (b) 7 (y+247)2+16x2=10247
- (c) x=8 cosθ4+3 sinθ, y=8 sinθ4+3 sinθ
r=105+4cosθ
r=93−6cosθ
- (a) Hyperbola
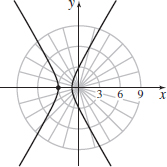
- (b) 3(x+2)2−y2=3
- (c) x=9 cosθ3−6 cosθ, y=9 sinθ3−6 cosθ
r=124+8sinθ
r(3−2sinθ)=6
- (a) Ellipse
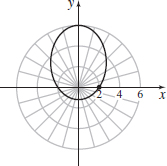
- (b) 9x2+5 (y−125)2=3245
- (c) x=6 cosθ3−2 sinθ, y=6 sinθ3−2 sinθ
r(2−cosθ)=2
r=6secθ2secθ−1
- (a) Ellipse
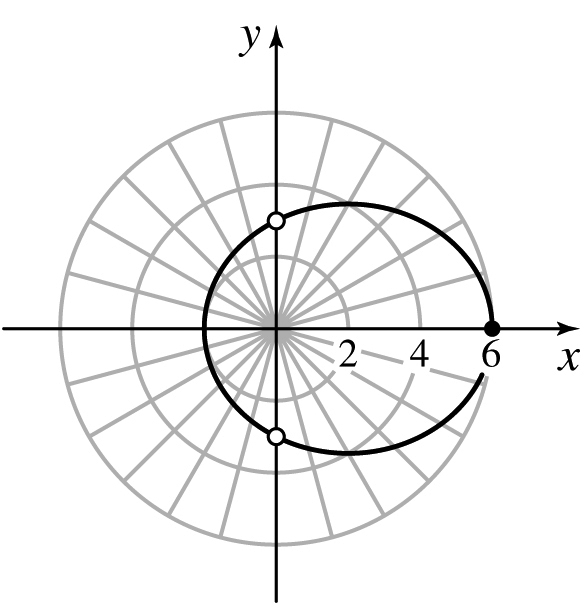
- (b) 4y2+3(x−2)2=48
- (c) x=6 cosθ2−cosθ, y=6 sinθ2−cosθ
r=3cscθcscθ−1
Applications and Extensions
In Problems 21–26, find the slope of the tangent line to the graph of each conic at θ.
r=\dfrac{9}{4-\cos \theta }, \theta =0
undefined
r=\dfrac{3}{1-\sin \theta }, \theta =0
r=\dfrac{8}{4+\sin \theta }, \theta =\dfrac{\pi }{2}
0
r=\dfrac{10}{5+4 \sin \theta }, \theta =\pi
r( 2+\cos \theta ) =4, \theta =\pi
undefined
r( 3-2 \sin \theta ) =6, \theta =\dfrac{\pi }{2}
In Problems 27–32, find a polar equation for each conic. For each equation, a focus is at the pole.
e=\dfrac{4}{5}; directrix is perpendicular to the polar axis 3 units to the left of the pole.
r=\dfrac{12}{5-4\ \cos\theta}
e=\dfrac{2}{3}; directrix is parallel to the polar axis 3 units above the pole.
e=1; directrix is parallel to the polar axis 1 unit above the pole.
r=\dfrac{1}{1+\sin\theta}
e=1; directrix is parallel to the polar axis 2 units below the pole.
e=6; directrix is parallel to the polar axis 2 units below the pole.
r=\dfrac{12}{1-6\ \sin\theta}
e=5; directrix is perpendicular to the polar axis 3 units to the right of the pole.
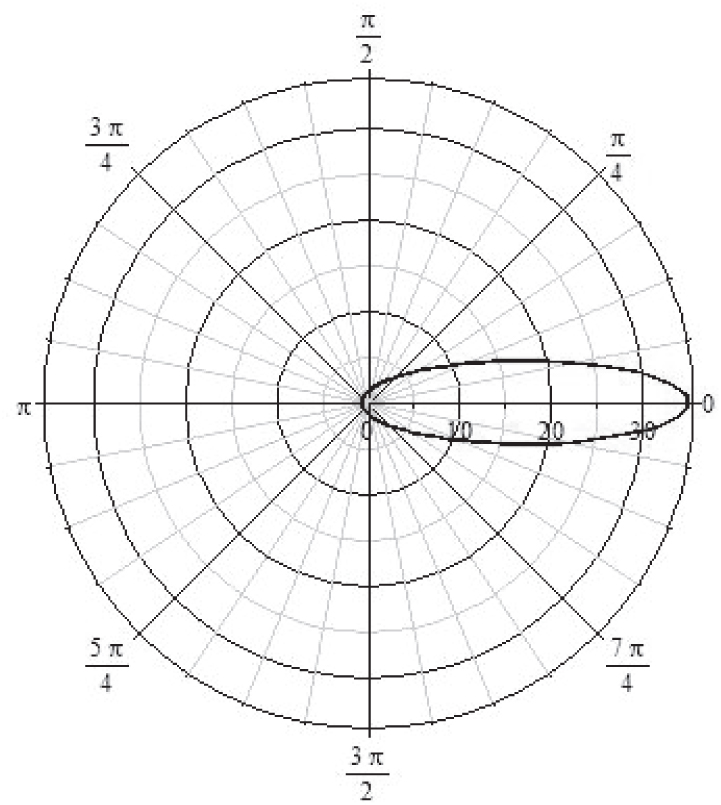
Halley’s Comet As with most comets, Halley’s comet has a highly elliptical orbit about the Sun, given by the polar equation r=\dfrac{1.155}{1-0.967 \cos \theta }
where the Sun is at the pole, the semimajor axis is along the polar axis, and r is measured in AU (astronomical unit). One \hbox{AU} =1.5\times 10^{11} {m}, which is the average distance from Earth to the Sun.

- (a) What is the eccentricity of the comet’s orbit?
- (b) Find the distance from Halley’s comet to the Sun at perihelion (shortest distance from the Sun).
- (c) Find the distance from Halley’s comet to the Sun at aphelion (greatest distance from the Sun).
- (d)
 Graph the orbit of Halley’s comet.
Graph the orbit of Halley’s comet.
- (a) 0.967
- (b) 0.587 AU
- (c) 35 AU
- (d)
Orbit of Mercury The planet Mercury travels around the Sun in an elliptical orbit given approximately by \begin{equation*} r=\dfrac{\left( 3.442\right) 10^{7}}{1-0.206 \cos \theta } \end{equation*}
where r is measured in miles and the Sun is at the pole.
- (a) What is the eccentricity of Mercury’s orbit?
- (b) Find the distance from Mercury to the Sun at perihelion (shortest distance from the Sun).
- (c) Find the distance from Mercury to the Sun at aphelion (greatest distance from the Sun).
- (d)
 Graph the orbit of Mercury.
Graph the orbit of Mercury.
 The Effect of Eccentricity
The Effect of Eccentricity- (a) Graph the conic r=\dfrac{2e}{1-e\cos \theta } for the following values of e: (i) e=0.2, (ii) e=0.6, (iii) e=0.9, (iv) e=1, (v) e=2, (vi) e=4.
- (b) Describe how the shape of the conic changes as e>1 gets larger.
- (c) Describe how the shape of the conic changes as e<1 gets closer to 0.
- (a) See Student Solutions Manual.
- (b) Answers will vary.
- (c) Answers will vary.
Show that the polar equation for a conic with its focus at the pole and whose directrix is perpendicular to the polar axis at a distance p units to the right of the pole is given by r=\dfrac{ep}{1+e\cos \theta }
Show that the polar equation for a conic with its focus at the pole and whose directrix is parallel to the polar axis at a distance p units above the pole is given by r=\dfrac{ep}{1+e\sin \theta }.
See Student Solutions Manual.
Show that the polar equation for a conic with its focus at the pole and whose directrix is parallel to the polar axis at a distance p units below the pole is given by r=\dfrac{ep}{1-e\sin \theta }.
Challenge Problems
Show that the surface area of the solid generated by revolving the first-quadrant arc of the ellipse \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1,\;x\geq 0,\;y\geq 0, about the x-axis is \begin{equation*} S=\pi b^{2}+\frac{\pi ab}{e}~\sin ^{-1}e \end{equation*}
where e is the eccentricity of the ellipse.
See Student Solutions Manual.
In this section, one focus of each conic has been at the pole. Write the general equation for a conic in polar coordinates if there is no focus at the pole. That is, suppose the focus F has polar coordinates (r_{1}, \theta _{1}), and the directrix D is given by r\cos (\theta +\theta _{0})=-d, where d>0. Let the eccentricity be e.
