REVIEW EXERCISESPrinted Page 9999
In Problems 1–6:
(a) Find the rectangular equation of each curve.
(b) Graph each plane curve whose parametric equations are given and show its orientation.
(c) Determine the restrictions on x and y that make the rectangular equation identical to the plane curve.
x(t)=4t−2,y(t)=1−t;−∞<t<∞
- (a) x=−4y+2
- (b)

- (c) No restrictions
x(t)=2t2+6,y(t)=5−t;−∞<t<∞
x(t)=et,y(t)=e−t−∞<t<∞
- (a) y=1x
- (b)

- (c) x≥0, y≥0
x(t)=lnt,y(t)=t3;t>0
x(t)=sec2t,y(t)=tan2t;0≤t≤π4
- (a) y+1=x
- (b)

- (c) 1≤x≤2, 0≤y≤1
x(t)=t3/2,y(t)=2t+4;t≥0
In Problems 7–10, for the parametric equations below:
(a) Find an equation of the tangent line to the curve at t.
(b) Graph the curve and the tangent line.
x(t)=t2−4,y(t)=tatt=1
- (a) y=12x+52
- (b)
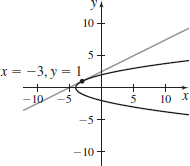
x(t)=3sint,y(t)=4cost+2att=π4
x(t)=1t2,y(t)=√t2+1att=3
- (a) y=−812√10x+92√10+√10
- (b)
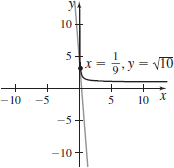
x(t)=t21+t,y(t)=t1+tatt=0
In Problems 11 and 12, find two different pairs of parametric equations for each rectangular equation.
y=−2x+4
Answers will vary.
y=2x
Describe the motion of an object that moves so that at time t (in seconds) it has coordinates x(t)=2cost,y(t)=sint,0≤t≤2π.
x24+y=1
In Problems 14–17, the polar coordinates of a point are given. Plot each point in a polar coordinate system, and find its rectangular coordinates.
(3,π6)
(−2,4π3)
(1,√3)
(3,−π2)
(−4,−π4)
(−2√2,2√2)
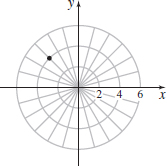
In Problems 18–21, the rectangular coordinates of a point are given. Find two pairs of polar coordinates (r,θ) for each point, one with r>0 and the other with r<0,0≤θ<2π.
(2,0)
(3,4)
(5,0.927), (−5,4.068)
(−5,12)
(−3,3)
(3√2,3π4),(−3√2,7π4)
In Problems 22–27, the letters r,θ represent polar coordinates. Write each equation in terms of the rectangular coordinates x,y.
r=4sin(2θ)
r=eθ/2
y=xtan ln(x2+y2)
r=11+2cosθ
r=a−sinθ
x2+y2=a√x2+y2−y
r2=4cos(2θ)
r=θ
y=x tan√x2+y2
In Problems 28–31, the letters x,y represent rectangular coordinates. Write each equation in terms of the polar coordinates r,θ.
x2+y2=x
(x2+y2)2=x2−y2
cos2θ−sin2θ=r2,r≠0
y2=(x2+y2)cos2[(x2+y2)1/2]
x222+y232=1
r=6√9 cos2θ+4 sin2θ9 cos2θ+4 sin2θ
In Problems 32–35, identify and graph each polar equation. Convert it to a rectangular equation if necessary.
rsinθ=1
rsecθ=2
The circle centered at (1, 0) of radius 1.
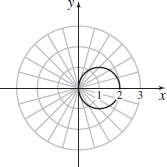
r=sinθ
r=−5cosθ
The circle centered at (−52,0) of radius 52.
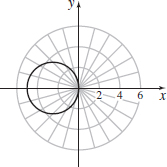
In Problems 36–45, for each equation:
(a) Graph the equation.
(b) Find parametric equations that represent the equation.
r=1−sinθ
r=4cos(2θ)
- (a)

- (b) x=4 cos(2θ)cosθ , y=4 cos(2θ)sinθ
r=12−sinθ
r=41−2cosθ
- (a)
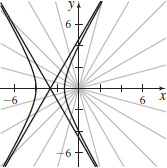
- (b) x=4 cosθ1−2 cosθ, y=4 sinθ1−2 cosθ
r=4sin(3θ)
r=2−2cosθ
- (a)
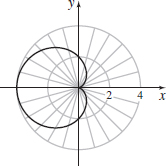
- (b) x=(2−2 cosθ)cosθ ,
y=(2−2 cosθ)sinθ
r=2−sinθ
r=e0.5θ
- (a)

- (b) x=e0.5θ cosθ,
y=e0.5θ sinθ
r2=1−sin2θ
r2=1+sin2θ
- (a)

- (b) x=√1+sin2θcosθ,
y=√1+sin2θsinθ
In Problems 46 and 47, for each polar equation:
(a) Identify and graph the equation.
(b) Convert the polar equation to a rectangular equation.
(c) Find parametric equations for the polar equation.
r=21−cosθ
r=11−16cosθ
- (a) An ellipse
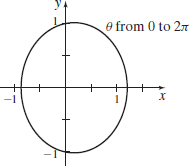
- (b) 35(x−635)2+36y2=129635
- (c) x=6 cosθ6−cosθ, y=6 sinθ6−cosθ
In Problems 48 and 49, find parametric equations for an object that moves along the ellipse x216+y29=1 with the motion described.
The motion begins at (4,0), is counterclockwise, and requires 4 seconds for a complete revolution.
The motion begins at (0,3), is clockwise, and requires 5 seconds for a complete revolution.
x=4 sin (2πt5), y=3 cos (2πt5), 0<t<5
In Problems 50 and 51, find the points (if any) on the curve at which the tangent line is vertical or horizontal.
x(t)=t3−1,y(t)=2t2+1
x(t)=1−sint,y(t)=2+3cost,0≤t≤2π
Vertical: (0,2), (2,2); horizontal: (1,5), (1,−1)
In Problems 52–55, find the arc length of each plane curve.
x(t)=sinh−1t,y(t)=√t2+1fromt=0tot=1
x(t)=tant,y(t)=13(sec2t+1)fromt=0tot=π4
s=13√132+98ln(1+√132)−98ln(√132)
x(t)=et,y(t)=12e2t−14tfromt=0tot=2
x=12y2−14lnyfromy=1toy=2
s=32+14ln2
In Problems 56–59, find the arc length of each curve represented by a polar equation.
r=2sinθfromθ=0toθ=π
r=e−θfromθ=0toθ=2π
√2(1−e−2π)
r=3θfromθ=0toθ=2π
r=2sin2θ2fromθ=−π2toθ=π2
2(4−2√2)
Area Find the area of the region inside the circle r=4sinθ and above the line r=3cscθ.
Area Find the area of the region that lies inside the rose r=4cos(2θ) and outside the circle r=√2.
2√7+12cos−1√24
Area Find the area of the region common to the graphs of r=cosθ and r=1−cosθ.
Surface Area Find the surface area of the solid generated by revolving the smooth curve represented by the parametric equations x(t)=sinh−1t,y(t)=√t2+1 from 0≤t≤1 about the x-axis.
π[√2+ln(1+√2)]
Surface Area Find the surface area of the solid generated by revolving the smooth curve represented by x(t)=et−t,y(t)=4et/2 from t=0 to t=1 about the x-axis.
Surface Area Find the surface area of the solid of revolution generated by revolving the curve represented by x=y2+1,0≤y≤2, about the y-axis.
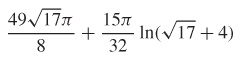
Surface Area Find the surface area of the solid generated by revolving the curve represented by y=cos(x2),0≤x≤π about the x-axis.
Surface Area Find the surface area of the solid of revolution generated by revolving the arc of the circle r=4,0≤θ≤π3, about the x-axis.
16π