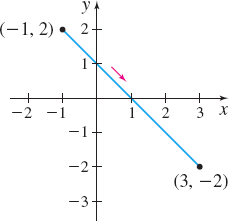9.1 Assess Your UnderstandingPrinted Page 643
Concepts and Vocabulary
Let x=x(t) and y=y(t) be two functions whose common domain is some interval I. The collection of points defined by (x,y)=(x(t),y(t)) is called a plane __________. The variable t is called a(n) __________.
Plane curve; parameter
Multiple Choice The parametric equations x(t)=2sint, y(t)=3cost define a(n) [(a) line, (b) hyperbola, (c) ellipse, (d) parabola].
(c)
Multiple Choice The parametric equations x(t)=asint, y(t)=acost, a>0, define a [(a) line, (b) hyperbola, (c) parabola, (d) circle].
(d)
If a circle rolls along a horizontal line without slipping, a point P on the circle traces out a curve called a(n) ______________.
Cycloid
True or False The parametric equations defining a curve are unique.
False
True or False Plane curves represented using parametric equations have an orientation.
True
Skill Building
In Problems 7–20:
(a) Find the rectangular equation of each plane curve with the given parametric equations.
(b) Graph the plane curve represented by the parametric equations and indicate its orientation.
x(t)=2t+1,y(t)=t+2;−∞<t<∞
- (a) x=2y−3
- (b)
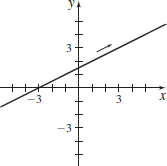
x(t)=t−2,y(t)=3t+1;−∞<t<∞
x(t)=2t+1,y(t)=t+2; 0≤t≤2
- (a) x=2y−3,1≤x≤5
- (b)
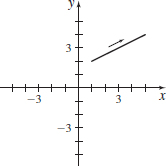
x(t)=t−2,y(t)=3t+1;0≤t≤2
x(t)=et,y(t)=t;−∞<t<∞
- (a) x=ey
- (b)
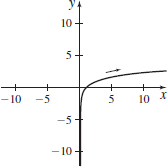
x(t)=t,y(t)=1t;−∞<t<∞,t≠0
x(t)=sint,y(t)=cost;0≤t≤2π
- (a) x2+y2=1
- (b)
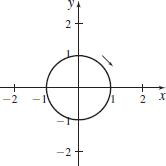
x(t)=cost,y(t)=sint;0≤t≤π
644
x(t)=2sint,y(t)=3cost; 0≤t≤2π
- (a) x24+y29=1
- (b)
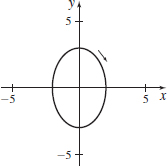
x(t)=4cost,y(t)=3sint;0≤t≤2π
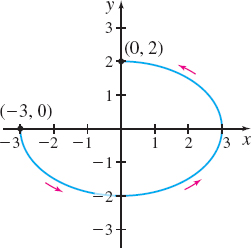
x(t)=2sint−3,y(t)=2cost+1;0≤t≤π
- (a) (x+3)24+(y−1)24=1
- (b)
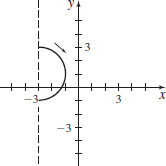
x(t)=4cost+1,y(t)=4sint−3;0≤t≤π
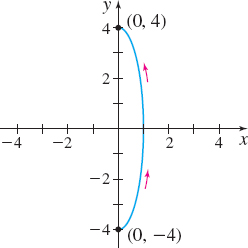
x(t)=3,y(t)=2t;−∞<t<∞
- (a) x=3
- (b)
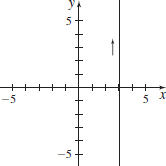
x(t)=4t+1, y(t)=2t;−∞<t<∞
In Problems 21–36:
(a) Find a rectangular equation of each plane curve with the given parametric equations.
(b) Graph the rectangular equation.
(c) Determine the restrictions on x and y so that the graph corresponding to the rectangular equation is identical to the plane curve.
(d) Graph the plane curve represented by the parametric equations.
x(t)=2,y(t)=t2+4;t>0
- (a) x=2
- (b)

- (c) x=2, y>4
- (d)
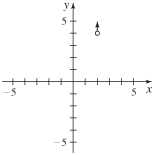
x(t)=t+3,y(t)=t3;−4≤t≤4
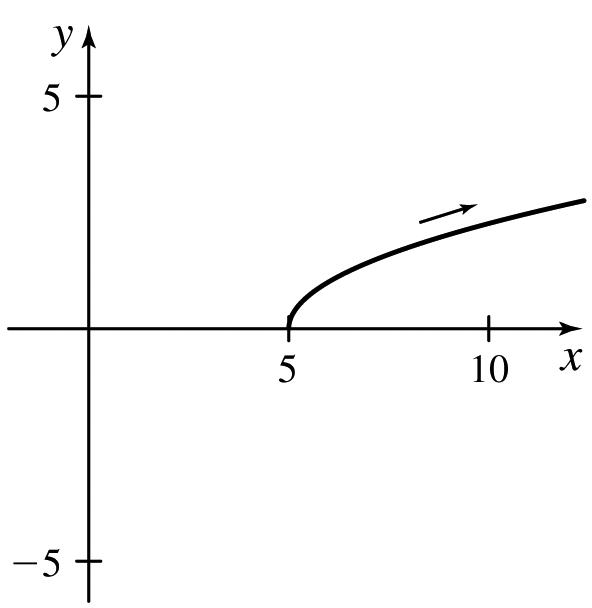
x(t)=t+5,y(t)=√t;t≥0
- (a) x=y2+5
- (b)
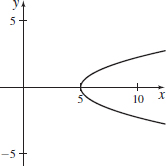
- (c) x≥5, y≥0
- (d)
x(t)=2t2,y(t)=2t3;0≤t≤3
x(t)=t1/2+1,y(t)=t3/2;t≥1
- (a) y=(x−1)3
- (b)
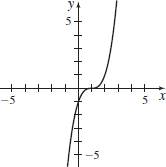
- (c) x≥2, y≥1
- (d)
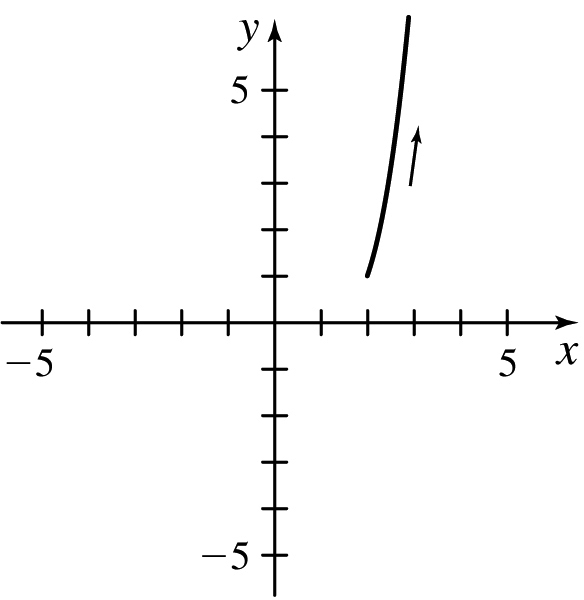
x(t)=2et,y(t)=1−et;t≥0
x(t)=sect,y(t)=tant;−π2<t<π2
- (a) x=sectan−1y
- (b)
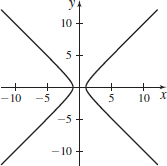
- (c) x≥1
- (d)
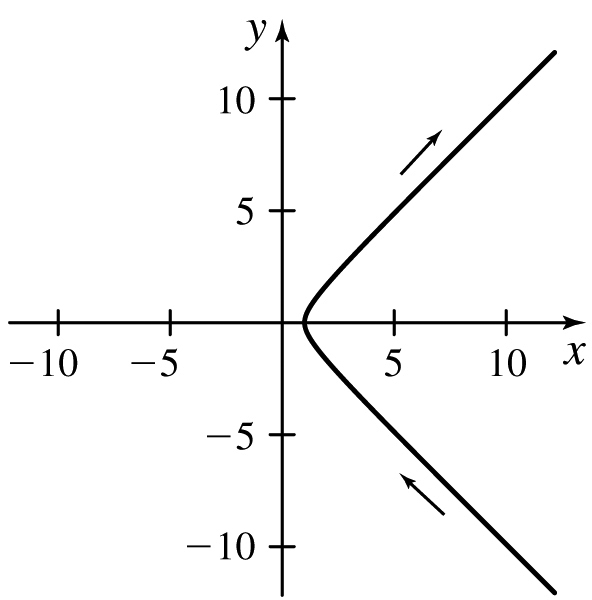
x(t)=3sinht,y(t)=2cosht;−∞<t<∞
x(t)=t4,y(t)=t2
- (a) x=y2
- (b)
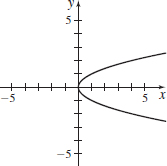
- (c) x≥0, y≥0
- (d)
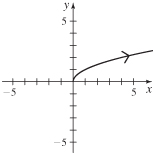
x(t)=t2,y(t)=t4
x(t)=t2,y(t)=2t−1
- (a) x=(y+12)2
- (b)
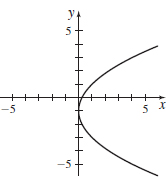
- (c) x≥0
- (d)

x(t)=e2t,y(t)=2et−1
x(t)=(1t)2,y(t)=2t−1
- (a) x=(y+12)2
- (b)
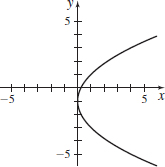
- (c) x>0,y≠−1
- (d)
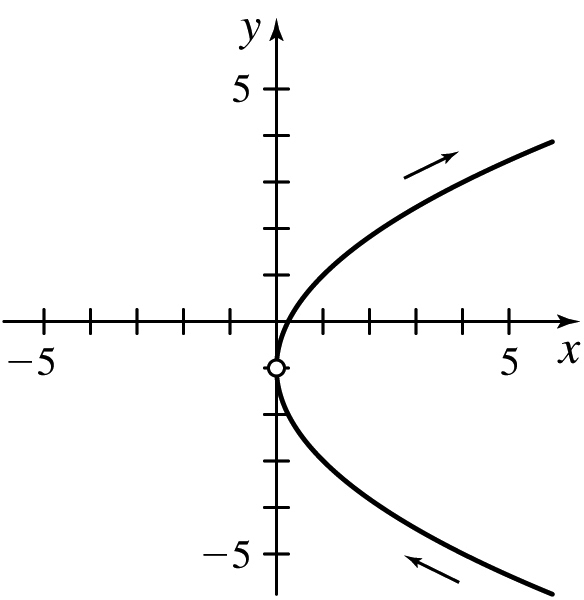
x(t)=t4,y(t)=2t2−1
 x(t)=3sin2t−2,y(t)=2cost;0≤t≤π
x(t)=3sin2t−2,y(t)=2cost;0≤t≤π
- (a) x+23+y24=1
- (b)
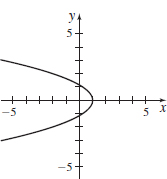
- (c) −2≤x≤1, −2≤y≤2
- (d)
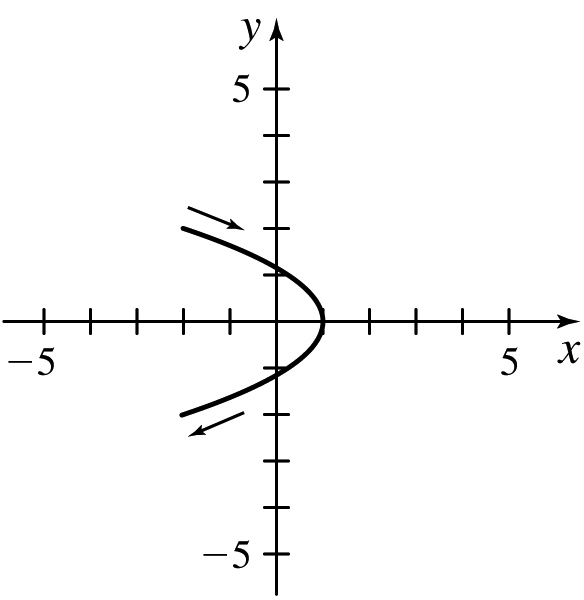
 x(t)=1+2sin2t,y(t)=2−cost;0≤t≤2π
x(t)=1+2sin2t,y(t)=2−cost;0≤t≤2π
Using Time as the Parameter In Problems 37–42, describe the motion of an object that moves along a curve so that at time t it has coordinates (x(t),y(t)).
x(t)=1t2,y(t)=2t2+1;t>0
y=2x1+x, x≥0, 0≤y≤2 Answers will vary.
x(t)=3t√t2+1,y(t)=3√t2+1
x(t)=4√4−t2,y(t)=4t√4−t2;0≤t<2
y=2√x2−4. Answers will vary.
x(t)=√t−3,y(t)=√t+1;t≥3
x(t)=sint−2,y(t)=4−2cost;0≤t≤2π
(x+2)2+(4−y2)2=1, −3≤x≤−1, 2≤y≤6 Answers will vary.
x(t)=2+tant,y(t)=3−2sect;−π/2<t<π/2
In Problems 43–50, find two different pairs of parametric equations corresponding to each rectangular equation.
y=4x−2
Answers will vary.
y=−8x+3
y=−2x2+1
Answers will vary.
y=x2+1
y=4x3
Answers will vary.
y=2x2
x=13√y−3
Answers will vary.
x=y3/2
In Problems 51–54, find parametric equations that represent the curve shown. The graphs in Problems 53 and 54 are parts of ellipses.
Answers will vary.
Answers will vary.
Motion of an Object In Problems 55–58, find parametric equations for an object that moves along the ellipse x29+y24=1, where the parameter is time (in seconds) if:
the motion begins at (3,0), is counterclockwise, and requires 3 seconds for 1 revolution.
x=3 cos2π3t, y=2 sin2π3t,0≤t≤3
the motion begins at (3,0), is clockwise, and requires 3 seconds for 1 revolution.
The motion begins at (0,2), is clockwise, and requires 2 seconds for 1 revolution.
x=3 sin(πt), y=2 cos(πt), 0≤t≤2
the motion begins at (0,2), is counterclockwise, and requires 1 second for 1 revolution.
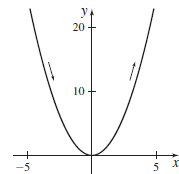
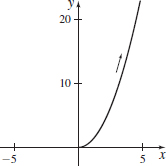
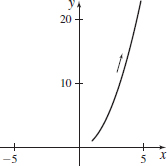
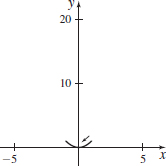
In Problems 59 and 60, the parametric equations of four plane curves are given. Graph each curve, indicate its orientation, and compare the graphs.
- (a) x(t)=t,y(t)=t2;−4≤t≤4
- (b) x(t)=√t, y(t)=t;0≤t≤16
- (c) x(t)=et, y(t)=e2t;0≤t≤ln4
- (d) x(t)=cost, y(t)=1−sin2t;0≤t≤π
- (a)
- (b)
- (c)
- (d)
- (a) x(t)=t, y(t)=√1−t2;−1≤t≤1
- (b) x(t)=sint, y(t)=cost;0≤t≤2π
- (c) x(t)=cost, y(t)=sint;0≤t≤2π
- (d) x(t)=√1−t2,y(t)=t;−1≤t≤1
645
Applications and Extensions
In Problems 61–64, the parametric equations of a plane curve and its graph are given. Match each graph in I–IV to the restricted domain given in a–d. Also indicate the orientation of each graph.

- (a) [−π2,π2]
- (b) [−π,π2]
- (c) [−π,0]
- (d) [0,π]

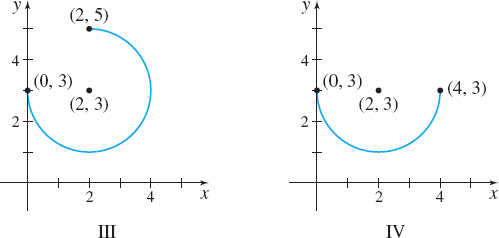
I→(d)counterclockwise, II→(a)counterclockwise, III→(b)counterclockwise, IV→(c)counterclockwise
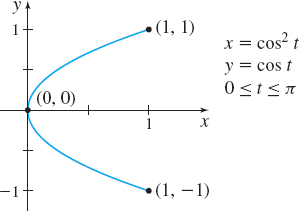
- (a) [π2,π]
- (b) [0,π3]
- (c) [0,π2]
- (d) [π3,π]
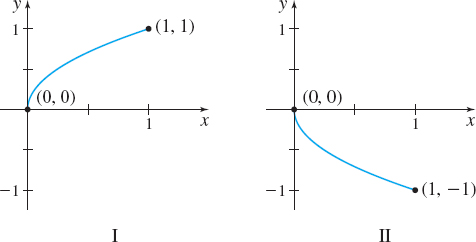
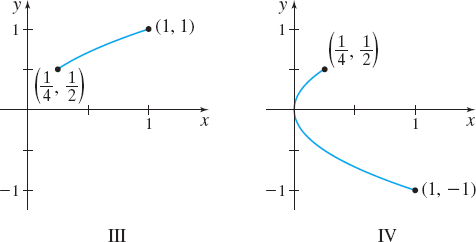
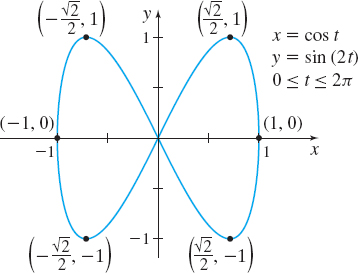
- (a) [π2,3π2]
- (b) [π,2π]
- (c) [0,π]
- (d) [5π4,2π]
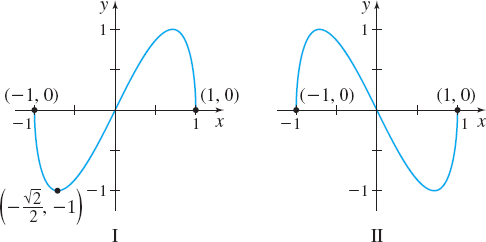

I→(c) from (1,0) to (−1,0), II→(b) from (−1,0) to (1,0), III→(a) clockwise, IV→(d) from (−√22,1) to (1,0)

646
- (a) [0,5π6]
- (b) [π,2π]
- (c) [0,π2]
- (d) [π6,5π6]
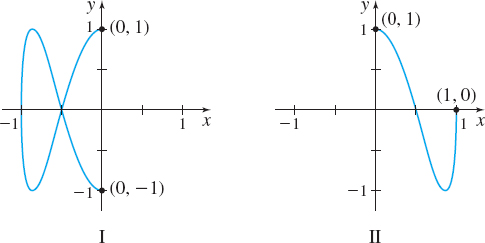
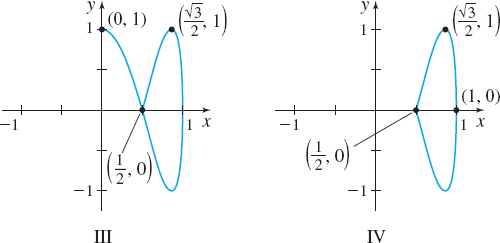

- (a) Graph the plane curve represented by the parametric equations x(t)=7(t−sint), y(t)=7(1−cost),0≤t≤2π.
- (b) Find the coordinates of the point (x,y) on the curve when t=2.1.
- (a)
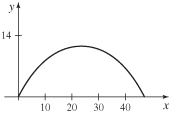
- (b) x≈8.66, y≈10.53

- (a) Graph the plane curve represented by the parametric equations x(t)=t−et,y(t)=2et/2,−8≤t≤2.
- (b) Find the coordinates of the point (x,y) on the curve when t=1.5.
Find parametric equations for the ellipse x2a2+y2b2=1.
Answers will vary.
Find parametric equations for the hyperbola x2a2−y2b2=1.
Problems 69–71 involve projectile motion. When an object is propelled upward at an inclination θ to the horizontal with initial speed v0, the resulting motion is called projectile motion. See the figure. Parametric equations that model the path of the projectile, ignoring air resistance, are given by x(t)=(v0cosθ)ty(t)=−12gt2+(v0sinθ)t+h
where t is time, g is the constant acceleration due to gravity (approximately 32ft/s2 or 9.8m/s2), and h is the height from which the projectile is released.
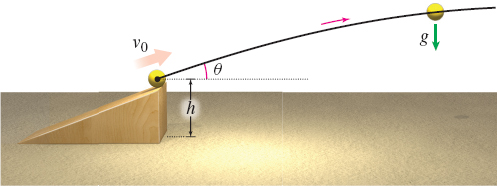
Trajectory of a Baseball A baseball is hit with an initial speed of 125ft/s at an angle of 40∘ to the horizontal. The ball is hit at a height of 3ft above the ground.
- (a) Find parametric equations that model the position of the ball as a function of the time t in seconds.
- (b) What is the height of the baseball after 2 seconds?
- (c) What horizontal distance x has the ball traveled after 2 seconds?
- (d) How long does it take the baseball to travel x=300ft?
- (e) What is the height of the baseball at the time found in (d)?
- (f) How long is the ball in the air before it hits the ground?
- (g) How far has the baseball traveled horizontally when it hits the ground?
- (a) x(t) = (125 cos 40°)t, y(t) = −16t2 + (125 sin 40°)t + 3
- (b) y≈99.6 ft
- (c) x≈191.5 ft
- (d) t≈3.13 s
- (e) y≈97.7 ft
- (f) t≈5.06 s
- (g) x≈484.5 ft
Trajectory of a Baseball A pitcher throws a baseball with an initial speed of 145ft/s at an angle of 20∘ to the horizontal. The ball leaves his hand at a height of 5ft.
- (a) Find parametric equations that model the position of the ball as a function of the time t in seconds.
- (b) What is the height of the baseball after 12 second?
- (c) What horizontal distance x has the ball traveled after 12 second?
- (d) How long does it take the baseball to travel x=60ft?
- (e) What is the height of the baseball at the time found in (d)?
Trajectory of a Football A quarterback throws a football with an initial speed of 80ft/s at an angle of 35∘ to the horizontal. The ball leaves the quarterback's hand at a height of 6ft.
- (a) Find parametric equations that model the position of the ball as a function of time t in seconds.
- (b) What is the height of the football after 1 second?
- (c) What horizontal distance x has the ball traveled after 1 second?
- (d) How long does it take the football to travel x=120ft?
- (e) What is the height of the football at the time found in (d)?
- (a) x(t) = (80 cos 35°)t, y(t) = −16t2 + (80 sin 35°)t + 6
- (b) y≈35.9 ft
- (c) x≈65.5 ft
- (d) t≈1.83 s
- (e) y≈36.4 ft
The plane curve represented by the parametric equations x(t)=t,y(t)=t2, and the plane curve represented by the parametric equations x(t)=t2,y(t)=t4 (where, in each case, time t is the parameter) appear to be identical, but they differ in an important aspect. Identify the difference, and explain its meaning.
The circle x2+y2=4 can be represented by the parametric equations x(θ)=2cosθ,y(θ)=2sinθ,0≤θ≤2π, or by the parametric equations x(θ)=2sinθ,y(θ)=2cosθ, 0≤θ≤2π. But the plane curves represented by each pair of parametric equations are different. Identify and explain the difference.
The first curve is counterclockwise from (2,0); the second is clockwise from (0,2). Answers will vary.
Uniform Motion A train leaves a station at 7:15 a.m. and accelerates at the rate of 3mi/h2. Mary, who can run 6mi/h, arrives at the station 2 seconds after the train has left. Find parametric equations that model the motion of the train and of Mary as a function of time. (Hint: The position s at time t of an object having acceleration a is s=12at2.)
647
Challenge Problems
Find parametric equations for the circle x2+y2=R2, using as the parameter the slope m of the line through the point (−R,0) and a general point P=(x,y) on the circle.
x=R(1−m2)1+m2, y=2Rm1+m2
Find parametric equations for the parabola y=x2, using as the parameter the slope m of the line joining the point (1,1) to a general point P=(x,y) on the parabola.
Hypocycloid Let a circle of radius b roll, without slipping, inside a fixed circle with radius a, where a>b. A fixed point P on the circle of radius b traces out a curve, called a hypocycloid, as shown in the figure. If A=(a,0) is the initial position of the point P and if t denotes the angle from the positive x-axis to the line segment from the origin to the center of the circle, show that the parametric equations of the hypocycloid are x(t)=(a−b)cost+bcos(a−bbt)y(t)=(a−b)sint−bsin(a−bbt)0≤t≤2π
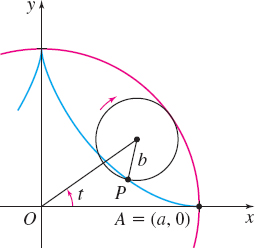
See Student Solutions Manual.
Hypocycloid Show that the rectangular equation of a hypocycloid with a=4b is x2/3+y2/3=a2/3.
Epicycloid Suppose a circle of radius b rolls on the outside of a second circle, as shown in the figure. Find the parametric equations of the curve, called an epicycloid, traced out by the point P.

x=(a+b) cost−b cos (a+bbt), y=(a+b) sint−b sin (a+bbt)