9.2 Assess Your UnderstandingPrinted Page 653
Concepts and Vocabulary
Multiple Choice Let C denote a curve represented by the parametric equations x=x(t), y=y(t), a≤t≤b, where each function x(t) and y(t) is continuous on the closed interval [a,b] and differentiable on the open interval (a,b). If both dxdt and dydt are continuous and never simultaneously 0 on (a,b), then C is called a [(a) smooth, (b) differentiable, (c) parametric] curve.
(a)
True or False If C is a smooth curve, represented by the parametric equations x=x(t) and y=y(t), a≤t≤b, then the slope of the tangent line to C at the point (x,y) is given by the formula dydx=dydtdxdt, provided dxdt≠0.
True
If in the formula for the slope of a tangent line, dydx=0 (butdxdt≠0), then the curve has a(n) ______________ tangent line at the point (x(t),y(t)). If dxdt=0 (butdydt≠0), then the curve has a(n) ______________ tangent line at the point (x(t),y(t)).
Horizontal; vertical
True or False For a smooth curve C represented by the parametric equations x=x(t), y=y(t), a≤t≤b, the length s of C from t=a to t=b is given by the formula s=∫ba√d2xdt2+d2ydt2 dt.
False
Skill Building
In Problems 5–12, find dydx. Assume dxdt≠0.
x(t)=etcost,y(t)=etsint
dydx=sint+costcost−sint
x(t)=1+e−t,y(t)=e3t
x(t)=t+1t,y(t)=4+t
dydx=11−1t2
x(t)=t+1t,y(t)=t−1t
x(t)=cost+tsint,y(t)=sint−tcost
dydx=tant
x(t)=cos3t,y(t)=sin3t
x(t)=cot2t,y(t)=cott
dydx=12cott
x(t)=sint,y(t)=sec2t
In Problems 13–26, for each pair of parametric equations:
(a) Find an equation of the tangent line to the curve at the given number.
(b) Graph the curve and the tangent line.
654
x(t)=2t2,y(t)=tatt=2
- (a) y=18x+1
- (b)
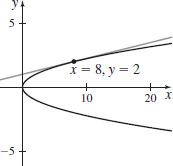
x(t)=t,y(t)=3t2att=−2
x(t)=3t,y(t)=2t2−1att=1
- (a) y=43x−3
- (b)
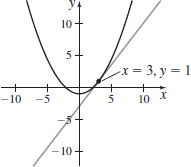
x(t)=2t,y(t)=t2−2att=2
x(t)=√t,y(t)=1tatt=4
- (a) y=−14x+34
- (b)
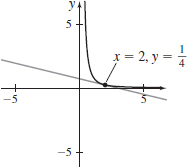
x(t)=2t2,y(t)=1tatt=1
x(t)=tt+2,y(t)=4t+2att=0
- (a) y=−2x+2
- (b)
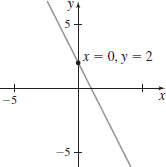
x(t)=t21+t,y(t)=11+tatt=0
x(t)=et,y(t)=e−tatt=0
- (a) y=−x+2
- (b)
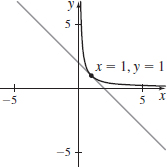
x(t)=e2t,y(t)=etatt=0
x(t)=sint,y(t)=costatt=π4
- (a) y=−x+√2
- (b)
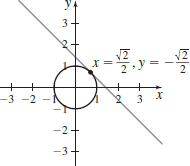
x(t)=sin2t,y(t)=costatt=π4
x(t)=4sint,y(t)=3costatt=π3
- (a) y=−3√34x+6
- (b)
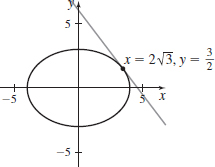
x(t)=2sint−1,y(t)=cost+2att=π6
In Problems 27–30, for each smooth curve, find any points where the tangent line is either horizontal or vertical.
x(t)=t2,y(t)=t3−4t
Horizontal at (43,−16√39), (43,16√39); vertical at (0,0)
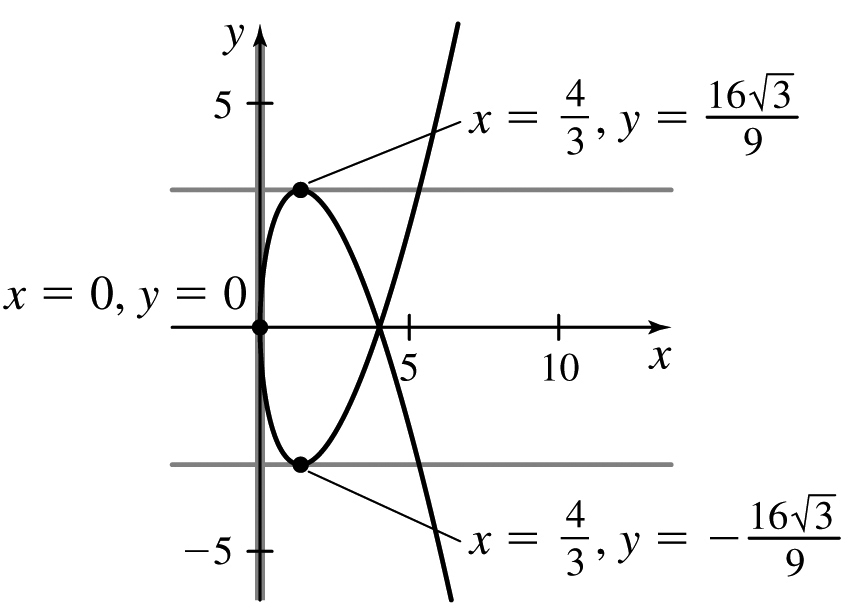
x(t)=t3−9t,y(t)=t2
x(t)=1−cost,y(t)=1−sint,0≤t≤2π
Horizontal at (1,0), (1,2); vertical at (0,1), (2,1)
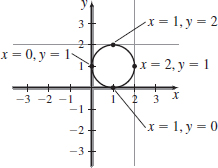
x(t)=−3cost+cos(3t),y(t)=sint,0≤t≤2π
In Problems 31–38, find the length of each curve over the given interval.
x(t)=t3,y(t)=t2;0≤t≤2
827(10√10−1)
x(t)=3t2+1,y(t)=t3−1;0≤t≤2
x(t)=t−1, y(t)=12t2;0≤t≤2
s=√5+12ln(2+√5)
x(t)=t2,y(t)=2t;1≤t≤3
x(t)=4sint,y(t)=4cost;−π2≤t≤π2
4π
x(t)=6sint,y(t)=6cost;−π2≤t≤π2
x(t)=2sint−1,y(t)=2cost+1;0≤t≤2π
4π
x(t)=etsint,y(t)=etcost;0≤t≤π
In Problems 39–44:
(a) Use the arc length formula for parametric equations to set up the integral for finding the length of each curve over the given interval.
(b) ![]() Find the length s of each curve over the given interval.
Find the length s of each curve over the given interval.
(c) ![]() Graph each curve over the given interval.
Graph each curve over the given interval.
x(t)=2cos(2t),y(t)=t2;0≤t≤2π
- (a) s=∫2π0√[−4 sin(2t)]2+(2t)2dt
- (b) s≈44.527
- (c)
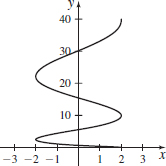
x(t)=t2,y(t)=sint;0≤t≤2π
x(t)=t2,y(t)=√t+2;−2≤t≤2
- (a) s=∫2−2√(2t)2+(12√t+2)2dt
- (b) s≈8.429
- (c)
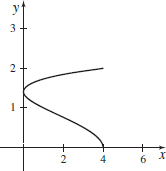
x(t)=t−cost,y(t)=1−sint;0≤t≤π
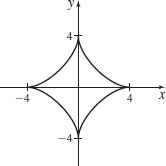
x(t)=3cost+cos(3t),y(t)=3sint−sin(3t);0≤t≤2π (a hypocycloid)
- (a) s=4⋅∫π/20√(−3 sint−3 sin(3t))2+(3 cost−3 cos(3t))2dt
- (b) s=24
- (c)
x(t)=5cost−cos(5t),y(t)=5sint−sin(5t);0≤t≤2π (an epicycloid)
Applications and Extensions
Tangent Lines
- (a) Find all the points on the plane curve C represented by x(t)=t2+2,y(t)=t3−4t, where the tangent line is horizontal or where it is vertical.
- (b) Show that C has two tangent lines at the point (6,0).
- (c) Find equations of these tangent lines.
- (d)
 Graph C.
Graph C.
- (a) Horizontal at (103,−16√39), (103,16√39); vertical at (2,0)
- (b) t=2, t=−2; see Student Solutions Manual
- (c) y=2x−12, y=−2x+12
- (d)

Tangent Lines
- (a) Find all the points on the plane curve C represented by x(t)=2t2, y(t)=8t−t3, where the tangent line is horizontal or where it is vertical.
- (b) Show that C has two tangent lines at the point (16,0).
- (c) Find equations of these tangent lines.
- (d)
 Graph C.
Graph C.
Arc Length
- (a) Find the arc length of one arch of the four-cusped hypocycloid x(t)=bsin3t,y(t)=bcos3t,0≤t≤π2.
- (b)
 Graph the portion of the curve for 0≤t≤π2.
Graph the portion of the curve for 0≤t≤π2.
- (a) s=3b2
- (b) b = 1
Arc Length
- (a) Find the arc length of the spiral x(t)=tcost,y(t)=tsint, 0≤t≤π.
- (b)
 Graph the portion of the curve for 0≤t≤π.
Graph the portion of the curve for 0≤t≤π.
Distance Traveled In Problems 49–54, find the distance a particle travels along the given path over the indicated time interval.
x(t)=3t,y(t)=t2−3;0≤t≤2
s=5+94ln3
x(t)=t2,y(t)=3t;0≤t≤2
x(t)=t22+1, y(t)=13(2t+3)3/2;0≤t≤2
s=3√11−√32+ln(3+√111+√3)
x(t)=acost, y(t)=asint;a>0,0≤t≤π
x(t)=cos(2t), y(t)=sin2t;0≤t≤π2
s=√5
x(t)=1t, y(t)=lnt;1≤t≤2
655
In Problems 55–57, find the speed at time t of an object moving along each curve.
x(t)=20t,y(t)=−16t2
√400+1024t2
x(t)=t+cost,y(t)=2t−sint
x(t)=20sin(2t),y(t)=6cost
√1600 cos2(2t)+36 sin2t
Arc Length along a Circle Use the arc length formula for parametric equations to show that for a circle of radius r, the length s of the arc subtended by a central angle of θ radians is s=rθ.
If the smooth curve C, represented by the parametric equations x=x(t),y=y(t), a≤t≤b, is the graph of a function y=f(x), then x can be used in place of the parameter t, and the parametric equations for C are x=t,y=f(t),a≤t≤b. Show that the arc length formula for these parametric equations takes the form s=∫ba√(dxdt)2+(dydt)2dt=∫ba√1+[f′(x)]2dx
See Student Solutions Manual.
Using Differentials to Approximate Arc Length Problems 60–63 use the following discussion:
For a smooth curve C represented by the parametric equations x=x(t),y=y(t), a≤t≤b, the arc length s satisfies the equation dsdt=√(dxdt)2+(dydt)2, so that (dsdt)2=(dxdt)2+(dydt)2. In terms of differentials, this can be written as (ds)2=(dx)2+(dy)2ds=√(dx)2+(dy)2
Geometrically, the differential ds=√(dx)2+(dy)2 is the length of the hypotenuse of a right triangle with sides of lengths dx and dy, as shown in the figure.
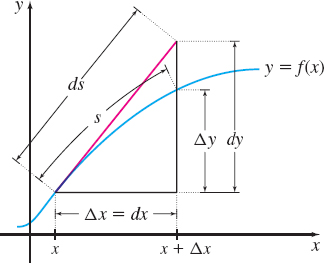
Because dydx is the slope of the tangent line, the hypotenuse lies on the tangent line to the curve at x. Then the differential ds can be used to approximate the arc length s between two nearby points. Using a differential to approximate arc length is particularly useful when it is difficult, or impossible, to find the arc length using s=∫ba√(dxdt)2+(dydt)2dt.
Use the differential ds to approximate each arc length.
x(t)=t1/3,y(t)=t2 from t=1 to t=1.1
x(t)=√t,y(t)=t3 from t=1 to t=1.2
0.73423
x(t)=asint,y(t)=bcost from t=0 to t=0.1
x(t)=eat,y(t)=ebt from t=0 to t=0.2
√e0.4a−2e0.2a+e0.4b−2e0.2b+2
Challenge Problems
Show that a smooth curve x=f(t),y=g(t), for which dxdt is never 0, can be represented by a rectangular equation y=F(x), where F is differentiable. [Hint: Use the fact that t=f−1(x) exists and is differentiable.]
Find the point on the curve x=43t3+3t2,y=t3−4t2, for which the length of the curve from (0,0) to (x,y) is 80√2−403.
(x(2),y(2))=(683,−8),(x(−2),y(−2))=(43,−24)
Higher-Order Derivatives Find an expression for d2ydx2 if x=f(t),y=g(t), where f and g have second-order derivatives, and dxdt is never 0.
Find d2ydx2 if x(θ)=acos3θ,y(θ)=asin3θ.
13a cos4θ sinθ
Consider the cycloid defined by x(t)=a(t−sint),y(t)=a(1−cost),a>0. Discuss the behavior of the tangent line to the cycloid at t=0.
