9.3 Assess Your UnderstandingPrinted Page 660
660
Concepts and Vocabulary
True or False When a smooth curve C represented by the parametric equations x=x(t), y=y(t), y≥0, a≤t≤b, is revolved about the x-axis, the surface area S of the solid of revolution is given by S=2π∫bax(t)√(dxdt)2+(dydt)2dt.
False
The surface area S of a solid of revolution generated by revolving the smooth curve C represented by x=x(t),y=y(t),a≤t≤b, where x(t)≥0, about the y-axis is S= ______________.
S=2π∫bax(t)√(dx/dt)2+(dy/dt)2dt
Skill Building
In Problems 3–14, find the surface area of the solid generated by revolving each curve about the x-axis.
x(t)=3t2,y(t)=6t;0≤t≤1
24π(2√2−1)
x(t)=t2,y(t)=2t;0≤t≤3
x(θ)=cos3θ,y(θ)=sin3θ;0≤θ≤π2
6π5
x(t)=t−sint, y(t)=1−cost;0≤t≤π
y=x3,0≤x≤1
π(10√10−1)27
y=4x3,0≤x≤2
y=x48+14x2,1≤x≤2
1179256π
y=√x;1≤x≤9
y=ex,0≤x≤1
π [e√1+e2−√2+ln (e+√1+e21+√2)]
y=e−x,0≤x≤1
y=√a2−x2,−a≤x≤a
4πa2
y=a2(ex/a+e−x/a),0≤x≤a
In Problems 15–20, find the surface area of the solid generated by revolving each curve about the y-axis.
x(t)=3t2,y(t)=2t3;0≤t≤1
245π(√2+1)
x(t)=2t+1, y(t)=t2+3;0≤t≤3
x(t)=2sint,y(t)=2cost;0≤t≤π2
8π
x(t)=3cost,y(t)=2sint;0≤t≤π2
x=14y2,0≤y≤2
2π (34√2+18ln (13+2√2))
x2/3+y2/3=a2/3;x≥0,0≤y≤a
Find the surface area of the solid generated by revolving one arch of the cycloid x(t)=6(t−sint), y(t)=6(1−cost) about the x -axis.
768π
 Find the surface area of the solid generated by revolving the graph of y=lnx, 1≤x≤10, about the x-axis.
Find the surface area of the solid generated by revolving the graph of y=lnx, 1≤x≤10, about the x-axis.
Applications and Extensions
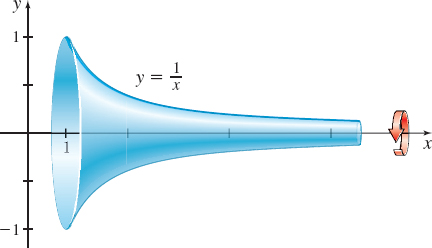
Gabriel’s Horn The surface formed by revolving the region between the graph of y=1x, x≥1, and the x-axis about the x-axis is called Gabriel’s horn. See the figure.
- (a) Find the surface area of Gabriel’s horn.
- (b) Find the volume of Gabriel’s horn.
Interesting Note: The volume of Gabriel’s horn is finite, but the surface area of Gabriel’s horn is infinite.
- (a) Infinite
- (b) π
Surface Area Find the surface area of the solid of revolution obtained by revolving the graph of y=e−x, x≥0, about the x-axis.
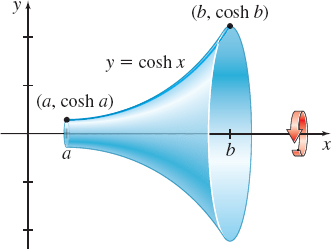
Surface Area of a Catenoid When an arc of a catenary y=coshx, a≤x≤b, is revolved about the x-axis, it generates a surface called a catenoid, which has the least surface area of all surfaces generated by rotating curves having the same endpoints. Find its surface area. See the figure.
π2[sinh(2b)−sinh(2a)]−π(b−a)
Surface Area of a Sphere Find a formula for the surface area of a sphere of radius R.
Surface Area Show that the surface area S of a right circular cone of altitude h and radius b is S=πb√h2+b2.
See Student Solutions Manual.
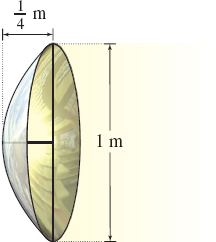
Challenge Problems
Searchlight The reflector of a searchlight is formed by revolving an arc of a parabola about its axis. Find the surface area of the reflector if it measures 1 m across its widest point and is 14 m deep.
661
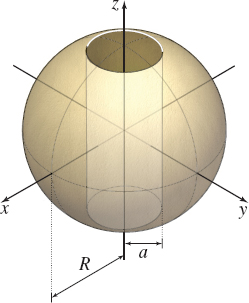
Surface Area of a Bead A sphere of radius R has a hole of radius a<R drilled through its center. The axis of the hole coincides with a diameter of the sphere. Find the surface area of the part of the sphere that remains.
S=4πR√R2−a2
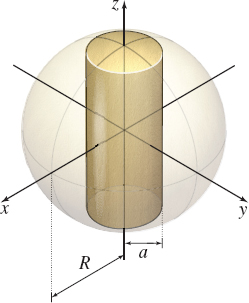
Surface Area of a Plug A plug is made to repair the hole in the sphere in Problem 29. What is the surface area of the plug?