
6.3 Gibbs Free Energy Is a Useful Thermodynamic Function for Understanding Enzymes
✓ 1 Describe the relations between the enzyme catalysis of a reaction, the thermodynamics of the reaction, and the formation of the transition state.
Enzymes speed up the rate of chemical reactions, but the properties of the reaction—
The Free-Energy Change Provides Information About the Spontaneity but Not the Rate of a Reaction
The free-
A reaction can take place spontaneously only if ΔG is negative. “Spontaneously” in the context of thermodynamics means that the reaction will take place without the input of energy and, in fact, the reaction releases energy. Such reactions are said to be exergonic.
A reaction cannot take place spontaneously if ΔG is positive. An input of free energy is required to drive such a reaction. These reactions are termed endergonic.
In a system at equilibrium, there is no net change in the concentrations of the products and reactants, and ΔG is zero.
Page 101The ΔG of a reaction depends only on the free energy of the products (the final state) minus the free energy of the reactants (the initial state). The ΔG of a reaction is independent of the path (or molecular mechanism) of the transformation. The mechanism of a reaction has no effect on ΔG. For example, the ΔG for the transformation of glucose into CO2 and H2O is the same whether it takes place by combustion or by a series of enzyme-
catalyzed steps in a cell. The ΔG provides no information about the rate of a reaction. A negative ΔG indicates that a reaction can take place spontaneously, but it does not signify whether it will proceed at a perceptible rate. As will be discussed shortly, the rate of a reaction depends on the free energy of activation (ΔG‡), which is largely unrelated to the ΔG of the reaction.
The Standard Free-Energy Change of a Reaction Is Related to the Equilibrium Constant
As for any reaction, we need to be able to determine ΔG for an enzyme-
Consider the reaction

The ΔG of this reaction is given by
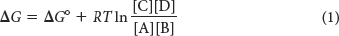
in which ΔG° is the standard free-
DID YOU KNOW?
A kilojoule (kJ) is equal to 1000 J.
A joule (J) is the amount of energy needed to apply a 1-
A kilocalorie (kcal) is equal to 1000 cal.
A calorie (cal) is equivalent to the amount of heat required to raise the temperature of 1 gram of water from 14.5°C to 15.5°C.
1 kJ = 0.239 kcal
A convention has been adopted to simplify free-
A simple way to determine the ΔG°′ is to measure the concentrations of reactants and products when the reaction has reached equilibrium. At equilibrium, there is no net change in the concentrations of reactants and products; in essence, the reaction has stopped and ΔG = 0. At equilibrium, equation 1 then becomes
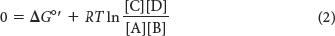
and so
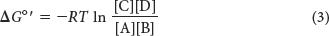
The equilibrium constant under standard conditions, 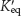 , is defined as
, is defined as

Substituting equation 4 into equation 3 gives

which can be rearranged to give

Substituting R = 8.315 × 10−3 kJ mol−1 K−1 and T = 298 K (corresponding to 25°C) gives

QUICK QUIZ
Which of the following two reactions will take place spontaneously? What are the ΔG°′ values for the reverse reactions?
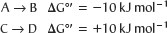
The reaction with the negative ΔG°′ will be spontaneous (exergonic), whereas the reaction with the positive ΔG°′ will not be spontaneous (endergonic). For the reverse reactions, the numerical values will be the same, but the signs of the reactions will be opposite.
where ΔG°′ is here expressed in kilojoules per mole because of the choice of the units for R in equation 7. Thus, the standard free energy and the equilibrium constant of a reaction are related by a simple expression. For example, an equilibrium constant of 10 gives a standard free-
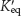 (at 25°C)
(at 25°C)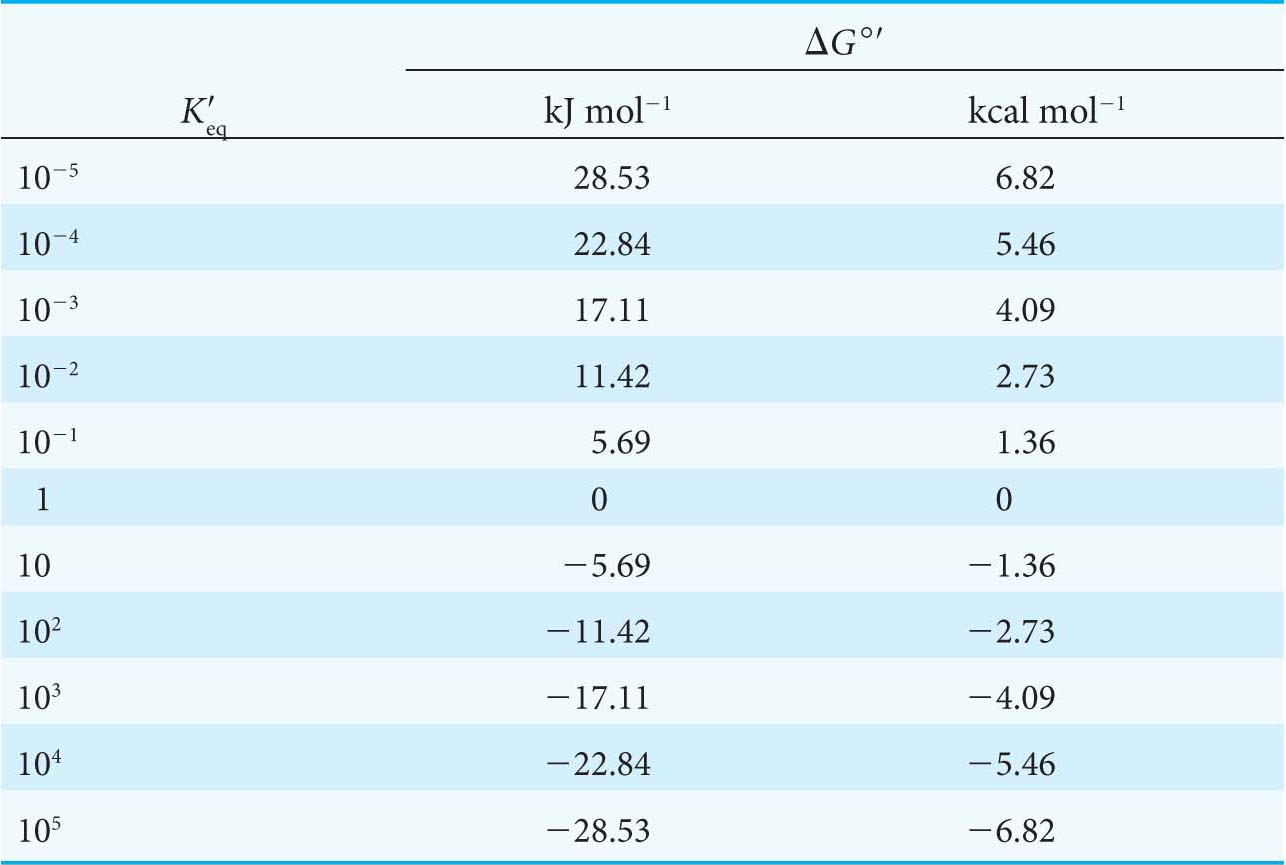
It is important to stress that whether the ΔG for a reaction is larger, smaller, or the same as ΔG°′ depends on the concentrations of the reactants and products. The criterion of spontaneity for a reaction is ΔG, not ΔG°′. This point is important because reactions that are not spontaneous, on the basis of ΔG°′, can be made spontaneous by adjusting the concentrations of reactants and products. This principle is the basis of the coupling of reactions to form metabolic pathways (Chapter 15).
Enzymes Alter the Reaction Rate but Not the Reaction Equilibrium
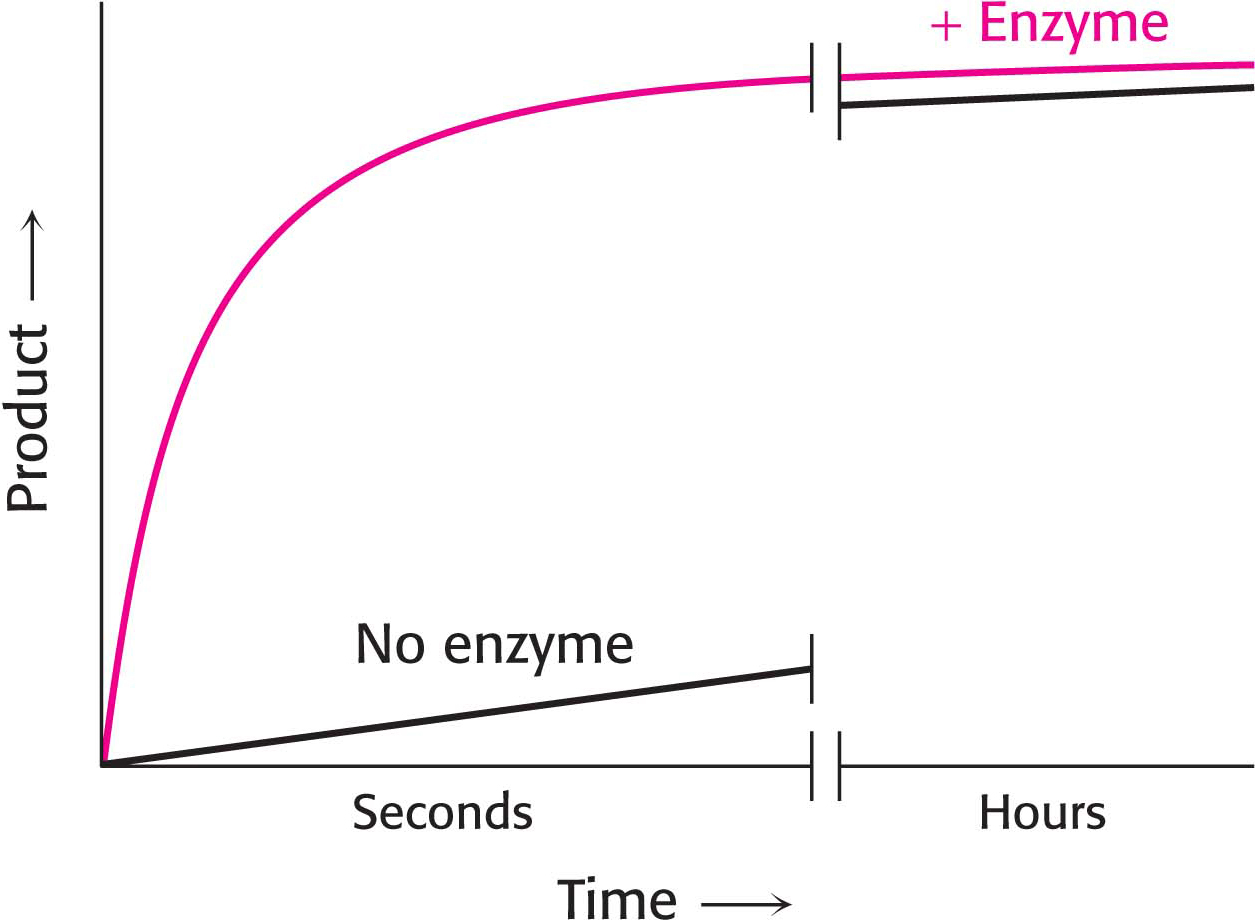
Because enzymes are such superb catalysts, it is tempting to ascribe to them powers that they do not have. An enzyme cannot alter the laws of thermodynamics and consequently cannot alter the equilibrium of a chemical reaction. Consider an enzyme-
Why does the rate of product formation level off with time? The reaction has reached equilibrium. Substrate S is still being converted into product P, but P is being converted into S at a rate such that the amount of P remains constant. Enzymes accelerate the attainment of equilibria but do not shift their positions. The equilibrium position is a function only of the free-