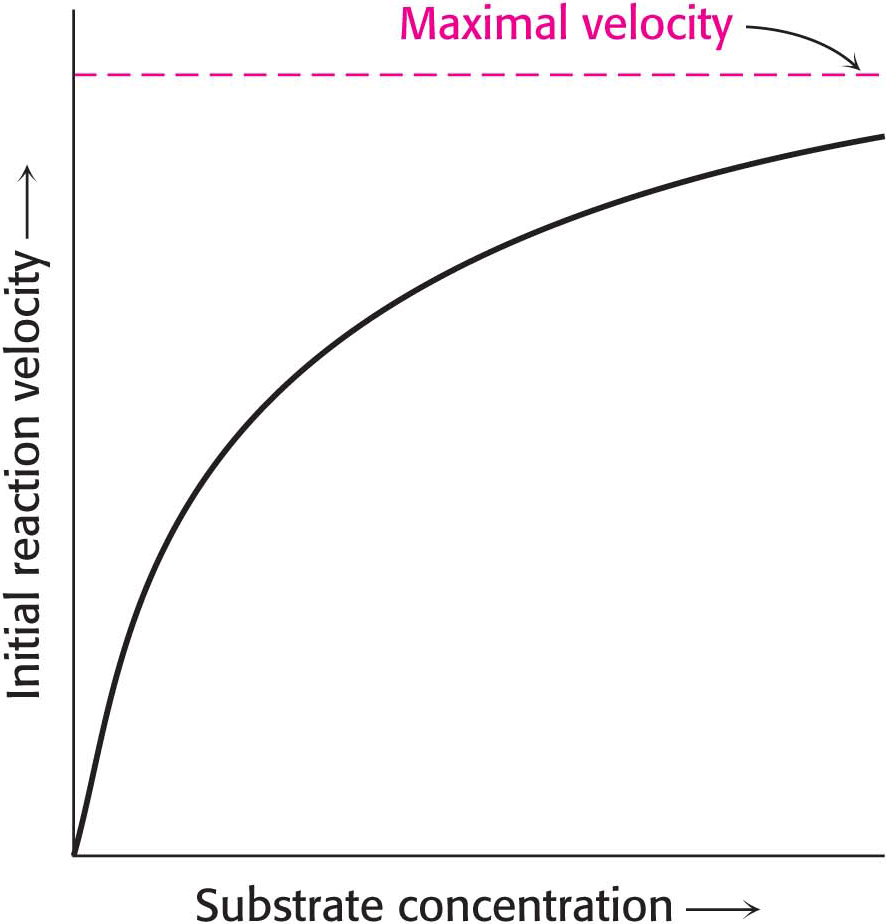
The initial velocity of catalysis, which is defined as the number of moles of product formed per second shortly after the reaction has begun, varies with the substrate concentration [S] when enzyme concentration is constant, in the manner shown in Figure 7.1. Examining how velocity changes in response to changes in substrate concentration is a reasonable way to study enzyme activity because variation in substrate concentration depends on environmental circumstances (for instance, after a meal), but enzyme concentration is relatively constant, especially on the time scale of reaction rates.

Before we can fully interpret this graph, we need to examine some of the parameters of the reaction. Consider an enzyme E that catalyzes the conversion of S into P by the following reaction:

where k₁ is the rate constant for the formation of the enzyme–substrate (ES) complex, k₂ is the rate constant for the formation of product P, and k₋₁ and k₋₂ are the constants for the respective reverse reactions. Figure 7.2 shows that the amount of product formed is determined as a function of time for a series of substrate concentrations. As expected, in each case, the amount of product formed increases with time, although eventually a time is reached when there is no net change in the concentration of S or P. The enzyme is still actively converting substrate into product and vice versa, but the reaction equilibrium has been attained.

We can simplify the entire discussion of enzyme kinetics if we ignore the reverse reaction of product forming substrate. We can define the rate of catalysis V₀, or the initial rate of catalysis, as the number of moles of product formed per second when the reaction is just beginning—that is, when t ≈ 0 and thus [P] ≈ 0. Thus, for the graph in Figure 7.2, V₀ is determined for each substrate concentration by measuring the rate of product formation at early times before P accumulates. With the use of this approximation, reaction 5 can be simplified to the following reaction scheme:

Enzyme E combines with substrate S to form an ES complex, with a rate constant k₁. The ES complex has two possible fates. It can dissociate to E and S, with a rate constant k₋₁, or it can proceed to form product P, with a rate constant k₂.

In 1913, on the basis of this reaction scheme and with some simple assumptions, Leonor Michaelis and Maud Menten proposed a simple model to account for these kinetic characteristics. The critical feature in their treatment is that a specific ES complex is a necessary intermediate in catalysis. The notion that an enzyme needed to bind substrate before catalysis could take place was not evident to the early biochemists. Some believed that enzymes might release emanations that converted substrate into product.

The Michaelis–Menten equation describes the variation of enzyme activity as a function of substrate concentration. The derivation of the equation from the terms just described can be found in the Appendix at the end of this chapter. This equation is

114

where

K_M, a compilation of rate constants called the Michaelis constant, is unique to each enzyme and is independent of enzyme concentration. K_M describes the properties of the enzyme–substrate interaction and thus will vary for enzymes that can use different substrates. The maximal velocity possible, V_max, can be attained only when all of the enzyme (total enzyme, or E_T) is bound to substrate (S):

V_max is directly dependent on enzyme concentration. Equation 7 describes the typical Michaelis–Menten curve as illustrated in Figure 7.3. At very low substrate concentrations, when [S] is much less than the value of K_M, the velocity is directly proportional to the substrate concentration; that is, V₀ = (V_max/K_M)[S]. At high substrate concentrations, when [S] is much greater than K_M, V₀ ≈ V_max; that is, the velocity is maximal, independent of substrate concentration. When an enzyme is operating at V_max, all of the available enzyme is bound to substrate; the addition of more substrate will not affect the velocity of the reaction. The enzyme is displaying zero-order kinetics. Under these conditions, the enzyme is said to be saturated.

Consider the circumstances when V₀ = V_max/2. Under these conditions, the practical meaning of K_M is evident from equation 7. Using V₀ = V_max/2, and solving for [S], we see that [S] = K_M at V₀ = V_max/2. Thus, K_M is equal to the substrate concentration at which the reaction velocity is half its maximal value. K_M is an important characteristic of an enzyme-catalyzed reaction and is significant for its biological function. Determination of V_max and K_M for an enzyme-catalyzed reaction is often one of the first characterizations of an enzyme undertaken.

115

K_M is equal to the substrate concentration that yields V_max/2; however, V_max, like perfection, is approached but never attained. How, then, can we experimentally determine K_M and V_max, and how do these parameters enhance our understanding of enzyme-catalyzed reactions? The Michaelis constant K_M and the maximal velocity V_max can be readily derived from rates of catalysis measured at a variety of substrate concentrations if an enzyme operates according to the simple scheme given in equation 7. The derivation of K_M and V_max is most commonly achieved with the use of curve-fitting programs on a computer. However, an older method is a source of further insight into the meaning of K_M and V_max.

Before the availability of computers, the determination of K_M and V_max values required algebraic manipulation of the basic Michaelis–Menten equation. The Michaelis–Menten equation can be transformed into one that gives a straightline plot. Taking the reciprocal of both sides of equation 7 gives the Lineweaver–Burk equation:

A plot of 1/V₀ versus 1/[S], called a double-reciprocal plot, yields a straight line with a y-intercept of 1/V_max and a slope of K_M/V_max (Figure 7.5). The intercept on the x axis is −1/K_M. This method is now rarely used because the data points at high and low concentrations are weighted differently and thus sensitive to errors.

The K_M values of enzymes range widely (Table 7.1). For most enzymes, K_M lies between 10⁻¹ and 10⁻⁷ M. The K_M value for an enzyme depends on the particular substrate and on environmental conditions such as pH, temperature, and ionic strength. The Michaelis constant K_M, as already noted, is equal to the concentration of substrate at which half the active sites are filled. Thus, K_M provides a measure of the substrate concentration required for significant catalysis to take place. For many enzymes, experimental evidence suggests that the K_M value provides an approximation of substrate concentration in vivo, which in turn suggests that most enzymes evolved to have significant activity at the substrate concentration commonly available. We can speculate about why an enzyme might evolve to have a K_M value that corresponds to the substrate concentration normally available to the enzyme. If the normal concentration of substrate is approximately equal to K_M, the enzyme will display significant activity and yet the activity will be sensitive to changes in environmental conditions—that is, changes in substrate concentration. At values below K_M, enzymes are very sensitive to changes in substrate concentration but display little activity. At substrate values well above K_M, enzymes have great catalytic activity but are insensitive to changes in substrate concentration. Thus, with the normal substrate concentration being approximately K_M, the enzymes have significant activity (1/2 V_max) but are still sensitive to changes in substrate concentration.

116

The maximal velocity V_max reveals the turnover number of an enzyme, which is the number of substrate molecules that an enzyme can convert into product per unit time when the enzyme is fully saturated with substrate. The turnover number is equal to the rate constant k₂, which is also called k_cat. If the total concentration of active sites, [E]_T, is known, then

and thus

For example, a 10⁻⁶ M solution of carbonic anhydrase catalyzes the formation of 0.6 M H₂CO₃ per second when the enzyme is fully saturated with substrate. Hence, k₂ is 6 × 10⁵ s⁻¹. This value is one of the largest known turnover numbers. Each catalyzed reaction takes place in a time equal to, on average, 1/k₂, which is 1.7 μs for carbonic anhydrase. The turnover numbers of most enzymes with their physiological substrates fall in the range from 1 to 10⁴ per second (Table 7.2).

When the substrate concentration is much greater than K_M, the velocity of catalysis approaches V_max. However, in the cell, most enzymes are not normally saturated with substrate. Under physiological conditions, the amount of substrate present is often between 10% and 50% K_M. Thus, the [S]/K_M ratio is typically between 0.01 and 1.0. When [S] ≪ K_M, the enzymatic rate is much less than k_cat (k₂) because most of the active sites are unoccupied. We can derive an equation that characterizes the kinetics of an enzyme under these cellular conditions:

When [S] ≪ K_M, almost all active sites are empty. In other words, the concentration of free enzyme, [E], is nearly equal to the total concentration of enzyme, [E]_T; so

Thus, when [S] ≪ K_M, the enzymatic velocity depends on the values of k_cat/K_M, [S], and [E]_T. Under these conditions, k_cat/K_M is the rate constant for the interaction of S and E. The rate constant k_cat/K_M, called the specificity constant, is a measure of catalytic efficiency because it takes into account both the rate of catalysis with a particular substrate (k_cat) and the nature of the enzyme–substrate interaction (K_M). For instance, by using k_cat/K_M values, we can compare an enzyme’s preference for different substrates. Table 7.3 shows the k_cat/K_M values for several different substrates of chymotrypsin, a digestive enzyme secreted by the pancreas. Chymotrypsin clearly has a preference for cleaving next to bulky, hydrophobic side chains.

117

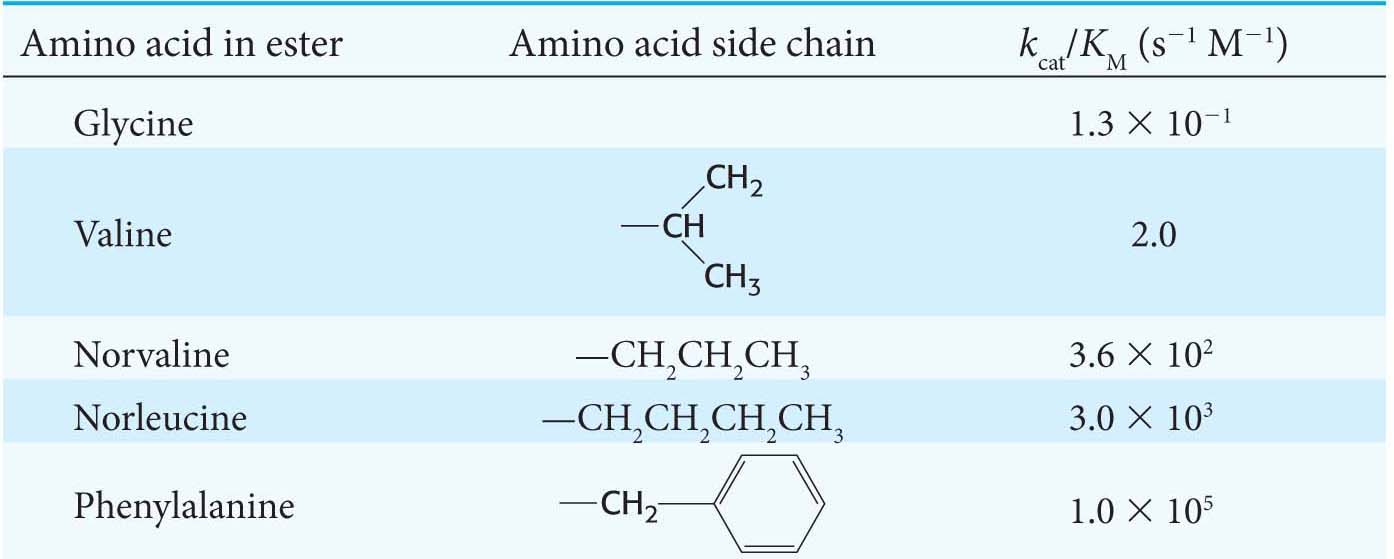
How efficient can an enzyme be? We can approach this question by determining whether there are any physical limits on the value of k_cat/K_M. Note that the k_cat/K_M ratio depends on k₁, k₋₁, and k_cat, as can be shown by substituting for K_M:

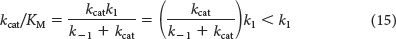
Suppose that the rate of formation of product (k_cat) is much faster than the rate of dissociation of the ES complex (k_–1). The value of k_cat/K_M then approaches k₁. Thus, the ultimate limit on the value of k_cat/K_M is set by k₁, the rate of formation of the ES complex. This rate cannot be faster than the diffusion-controlled encounter of an enzyme and its substrate. Diffusion limits the value of k₁, and so it cannot be higher than 10⁸ to 10⁹ s⁻¹ M⁻¹. Hence, the upper limit on k_cat/K_M is between 10⁸ and 10⁹ s⁻¹ M⁻¹.

The k_cat/K_M ratios of the enzymes superoxide dismutase, acetylcholinesterase, and triose phosphate isomerase are between 10⁸ and 10⁹ s⁻¹ M⁻¹. Enzymes that have k_cat/K_M ratios at the upper limits have attained kinetic perfection. Their catalytic velocity is restricted only by the rate at which they encounter substrate in the solution (Table 7.4).

The simplest way to explain Michaelis–Menten kinetics is to use a one-substrate reaction as an example. However, most reactions in biological systems start with two substrates and yield two products. They can be represented by the following bisubstrate reaction:

118

Many such reactions transfer a functional group, such as a phosphoryl or an ammonium group, from one substrate to the other. Those that are oxidation–reduction reactions transfer electrons between substrates. Although equations can be developed to describe the kinetics of multiple-substrate reactions, we will forego a kinetic description of such reactions and simply examine some general principles of bisubstrate reactions.

Multiple-substrate reactions can be divided into two classes: sequential reactions and double-displacement reactions (Figure 7.6). The depictions shown in Figure 7.6 are called Cleland representations.

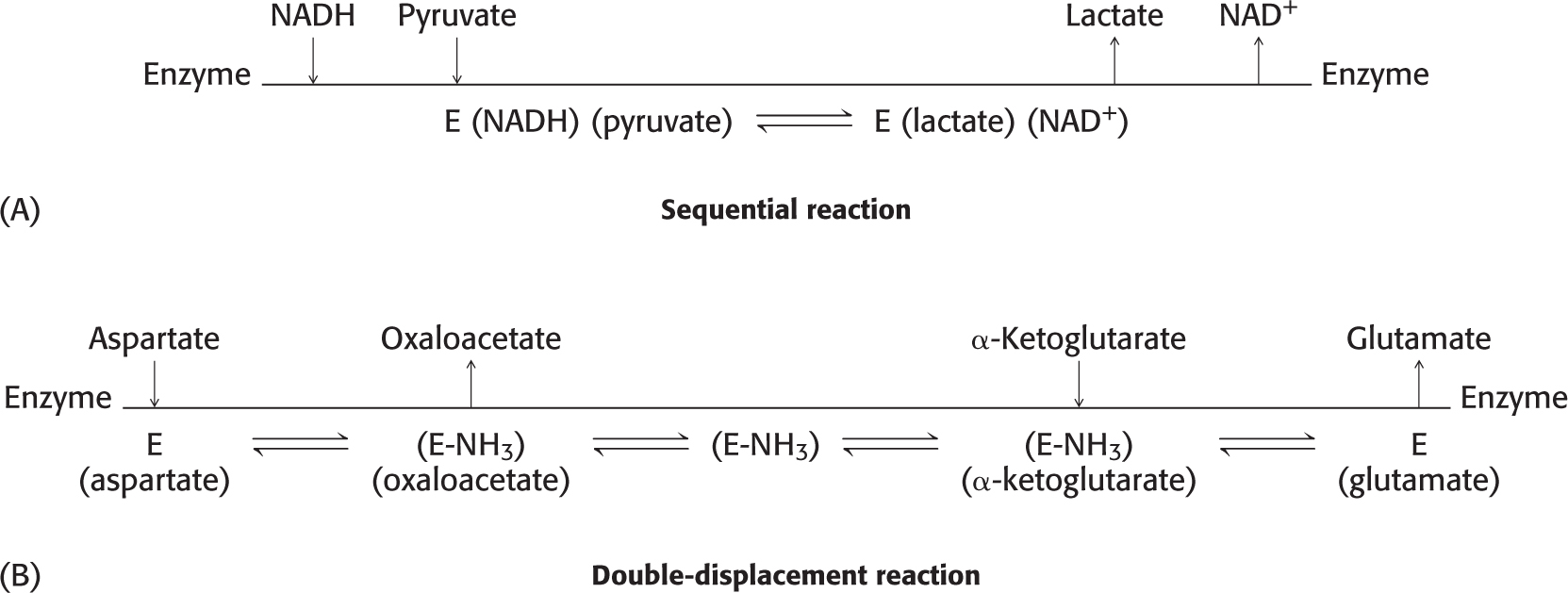
Sequential reactionsIn sequential reactions (Figure 7.6A), all substrates must bind to the enzyme before any product is released. Consequently, in a bisubstrate reaction, a ternary complex consisting of the enzyme and both substrates forms. Sequential mechanisms are of two types: ordered, in which the substrates bind the enzyme in a defined sequence, and random.

Double-displacement (ping-pong) reactionsIn double-displacement, or ping-pong, reactions (Figure 7.6B), one or more products are released before all substrates bind the enzyme. The defining feature of double-displacement reactions is the existence of a substituted enzyme intermediate, in which the enzyme is temporarily modified. Reactions that shuttle amino groups between amino acids and α-ketoacids are classic examples of double-displacement mechanisms. As shown in Figure 7.6, the substrates and products appear to bounce on and off the enzyme just as a Ping-Pong ball bounces on and off a table.