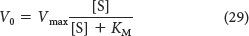As already discussed, the key feature of the Michaelis–Menten treatment of enzyme kinetics is that a specific enzyme–substrate (ES) complex is a necessary intermediate in catalysis. The model proposed is

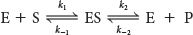
An enzyme E combines with substrate S to form an ES complex, with a rate constant k₁. The ES complex has two possible fates. It can dissociate to E and S, with a rate constant k₋₁, or it can proceed to form product P, with a rate constant k₂. The ES complex can also be re-formed from E and P by the reverse reaction with a rate constant k₋₂. However, as already discussed, we simplify these reactions by considering the velocity of reaction at times close to zero, when there is negligible product formation and thus no reverse reaction (k₋₂ [S][P] ≈ 0):

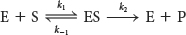
We want an expression that relates the velocity of catalysis to the concentrations of substrate and enzyme and the rates of the individual steps. Our starting point is that the catalytic velocity is equal to the product of the concentration of the ES complex and k₂:

Now we need to express [ES] in terms of known quantities. The rates of formation and breakdown of ES are given by

To simplify matters further, we use the steady-state assumption. In a steady state, the concentrations of intermediates—in this case, [ES]—stay the same even if the concentrations of starting materials and products are changing. This steady state is achieved when the rates of formation and breakdown of the ES complex are equal. Setting the right-hand sides of equations 17 and 18 equal gives

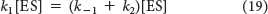
By rearranging equation 19, we obtain

126

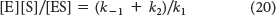
Equation 20 can be simplified by defining a new constant, K_M, called the Michaelis constant:

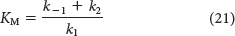
Note that K_M has the units of concentration and is independent of enzyme and substrate concentrations.

Inserting equation 21 into equation 20 and solving for [ES] yields

Now, let us examine the numerator of equation 22. Because the substrate is usually present at much higher concentration than the enzyme, the concentration of uncombined substrate [S] is very nearly equal to the total substrate concentration. The concentration of uncombined enzyme [E] is equal to the total enzyme concentration [E]_T minus the concentration of the ES complex:

Substituting this expression for [E] in equation 22 gives

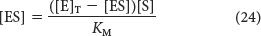
Solving equation 24 for [ES] gives

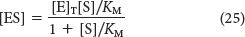
or

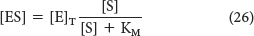
By substituting this expression for [ES] into equation 16, we obtain

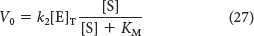
The maximal velocity V_max is attained when the catalytic sites on the enzyme are saturated with substrate—that is, when [ES] = [E]_T. Thus,

Substituting equation 28 into equation 27 yields the Michaelis–Menten equation: