12.4 Dot Product and the Angle between Two Vectors
The dot product is one of the most important vector operations. It plays a role in nearly all aspects of multivariable calculus.
DEFINITION Dot Product
The dot product \(\textbf{v}\cdot w\) of two vectors \[ \textbf{v}=\langle a_1,b_1,c_1\rangle,\qquad w= \langle a_2,b_2,c_2\rangle \]
is the scalar defined by \[ \boxed{ v\cdot w = a_1a_2+b_1b_2+c_1c_2} \]
Note
Important concepts in mathematics often have multiple names or notations either for historical reasons or because they arise in more than one context. The dot product is also called the “scalar product” or “inner product” and in many texts, \(\textbf{v}\cdot w\) is denoted \((v,w)\) or \(\langle v,w\rangle\).
In words, to compute the dot product, multiply the corresponding components and add. For example, \[ \langle 2,3,1\rangle\cdot \langle -4,2,5\rangle = 2(-4)+3(2)+1(5) = -8+6+5=3 \]
The dot product of vectors \(\textbf{v}=\langle a_1,b_1\rangle\) and \(w=\langle a_2,b_2\rangle\) in \(\textbf{R}^2\) is defined similarly: \[ \textbf{v}\cdot w = a_1a_2+b_1b_2 \]
We will see in a moment that the dot product is closely related to the angle between \(\textbf{v}\) and \(\textbf{w}\). Before getting to this, we describe some elementary properties of dot products.
679
First, the dot product is commutative: \(\textbf{v}\cdot w=w\cdot v\), because the components can be multiplied in either order. Second, the dot product of a vector with itself is the square of the length: If \({v = \langle a, b, c \rangle}\), then \[ \textbf{v}\cdot v = a\cdot a+b\cdot b+c\cdot c = a^2+b^2+c^2 = \parallel{v}\parallel^2 \]
The dot product also satisfies a Distributive Law and a scalar property as summarized in the next theorem (see Exercises 84 and 85).
Note
The dot product appears in a very wide range of applications. To rank how closely a Web document matches a search input at Google,
“We take the dot product of the vector of count-weights with the vector of type-weights to compute an IR score for the document.”
From “The Anatomy of a Large-Scale Hypertextual Web Search Engine” by Google founders Sergey Brin and Lawrence Page.
THEOREM 1 Properties of the Dot Product
- (i) \({0\cdot v=v\cdot v = 0}\)
- (ii) Commutativity: \(\textbf{v}\cdot w = w\cdot v\)
- (iii) Pulling out scalars:\(\quad {(\lambda v)\cdot w=v\cdot (\lambda w)=\lambda(v\cdot w)}\)
- (iv)] Distributive Law:\(\quad \begin{array}[t]{lcl} u\cdot (v+w) & {}={} & u\cdot v+u\cdot w \\ (v+w)\cdot u & =& v\cdot u+w\cdot u \\ \end{array}\)
- (v) Relation with length:\(\quad {v\cdot v={\parallel v \parallel}^2}\)
EXAMPLE 1
Verify the Distributive Law \(u\cdot (v+w) = u\cdot v+u\cdot w\) for \[ u = \langle 4,3,3 \rangle,\qquad v = \langle 1, 2, 2 \rangle,\qquad w = \langle 3, -2, 5 \rangle \]
Solution We compute both sides and check that they are equal: \begin{align*} u\cdot (v+w)& = \langle 4,3,3 \rangle\cdot \big(\langle 1, 2, 2 \rangle+\langle 3, -2, 5 \rangle\big) \\&= \langle 4,3,3 \rangle\cdot \langle 4, 0, 7 \rangle =4(4)+3(0)+3(7) = 37 \\ u\cdot v+u\cdot w & = \langle 4,3,3 \rangle\cdot \langle 1, 2, 2 \rangle+\langle 4,3,3 \rangle\cdot\langle 3, -2, 5 \rangle \\ &= \bigl(4(1)+3(2)+3(2)\bigr) + \bigl(4(3)+3(-2)+3(5)\bigr)\\ &= 16+ 21=37 \end{align*}
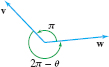
As mentioned above, the dot product \(\textbf{v}\cdot w\) is related to the angle \(\theta\) between \(\textbf{v}\) and \(\textbf{w}\). This angle \(\theta\) is not uniquely defined because, as we see in Figure 12.37, both \(\theta\) and \(2\pi-\theta\) can serve as an angle between \(\textbf{v}\) and \(\textbf{w}\). Furthermore, any multiple of \(2\pi\) may be added to \(\theta\). All of these angles have the same cosine, so it does not matter which angle we use in the next theorem. However, we shall adopt the following convention: \[ \boxed{ \textit{The angle between two vectors is chosen to satisfy \(0\le\theta \le \pi\)}.} \]
THEOREM 2 Dot Product and the Angle
Let \(\theta\) be the angle between two nonzero vectors \(\textbf{v}\) and \(\textbf{w}\). Then \begin{equation} \label{14.dotprod.prodangle} \boxed{ \textbf{v}\cdot w = \parallel{v}\parallel\,\parallel{w}\parallel\cos\theta\quad\textrm{or}\quad \cos\theta = \frac{v\cdot w}{\parallel{v}\parallel\,\parallel{w}\parallel}} \end{equation}
Proof
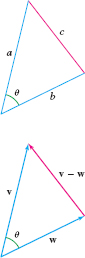
According to the Law of Cosines, the three sides of a triangle satisfy (Figure 12.38) \[ c^2 = a^2+b^2 - 2ab\cos\theta \]
680
If two sides of the triangle are \(\textbf{v}\) and \(\textbf{w}\), then the third side is \(\textbf{v}-w\), as in the figure, and the Law of Cosines gives \begin{equation}\label{14.dotprod.normsq} \parallel{v-w}\parallel^2 = \parallel{v}\parallel^2+\parallel{w}\parallel^2-2\cos\theta\parallel{v}\parallel\,\parallel{w}\parallel \end{equation}
Now, by property (v) of Theorem 1 and the Distributive Law, \begin{align} \parallel{v-w}\parallel^2 &= (v-w)\cdot (v-w)= v\cdot v-2v\cdot w + w\cdot w\notag\\ &=\parallel{v}\parallel^2+\parallel{w}\parallel^2-2v\cdot w\label{14.dotprod.cdot} \end{align}
Comparing Eq.(2) and Eq.(3), we obtain \({ -2\cos\theta\parallel{v}\parallel\,\parallel{w}\parallel = -2v\cdot w}\), and Eq.(1) follows.
By definition of the arccosine, the angle \(\theta=\cos^{-1}x\) is the angle in the interval \([0, \pi]\) satisfying \(\cos\theta=x\). Thus, for nonzero vectors \(\textbf{v}\) and \(\textbf{w}\), we have \[ \boxed{\theta = \cos^{-1}\left( \frac{v\cdot w}{ \parallel{v}\parallel\,\parallel{w}\parallel} \right) } \]
EXAMPLE 2
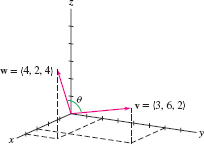
Find the angle \(\theta\) between \(\textbf{v} = \langle 3,6,2\rangle\) and \(w= \langle 4,2,4\rangle\).
Solution Compute \(\cos\theta\) using the dot product: \begin{eqnarray*} &\displaystyle \parallel{v}\parallel=\sqrt{3^2+6^2+2^2}=\sqrt{49}=7,\qquad \parallel{w}\parallel=\sqrt{4^2+2^2+4^2}=\sqrt{36}=6\\ &\displaystyle \cos\theta = \frac{v\cdot w}{\parallel{v}\parallel\parallel{w}\parallel} = \frac{\langle 3,6,2\rangle\cdot \langle 4,2,4\rangle}{7\cdot 6} = \frac{3\cdot 4+6\cdot 2+ 2\cdot 4}{42} = \frac{32}{42} = \frac{16}{21} \end{eqnarray*}
The angle itself is \(\theta = \cos^{-1}\big(\frac{16}{21}\big) \approx 0.705\) rad (Figure 12.39).
Note
The terms “orthogonal” and “perpendicular” are synonymous and are used interchangeably, although we usually use “orthogonal” when dealing with vectors.
Two nonzero vectors \(\textbf{v}\) and \(\textbf{w}\) are called perpendicular or orthogonal if the angle between them is \(\frac{\pi}2\). In this case we write \(\textbf{v}\perp w\).
We can use the dot product to test whether \(\textbf{v}\) and \( w\) are orthogonal. Because an angle between \(0\) and \(\pi\) satisfies \(\cos\theta=0\) if and only if \(\theta = \frac{\pi}2\), we see that \[ \textbf{v}\cdot w = \parallel{v}\parallel\,\parallel{w}\parallel\cos\theta = 0\quad \Leftrightarrow\quad \theta = \frac{\pi}2 \]
and thus \[ \boxed{\textrm{\(\textbf{v}\perp w\quad\) if and only if \(\quad v\cdot w = 0\)}} \]
The standard basis vectors are mutually orthogonal and have length 1 (Figure 12.40). In terms of dot products, because \(i = \langle 1,0,0\rangle\), \( j = \langle 0,1,0\rangle\), and \(k = \langle 0,0,1\rangle\), \[ i\cdot j = i\cdot k=j\cdot k=0,\quad\qquad i\cdot i=j\cdot j=k\cdot k=1 \]
EXAMPLE 3 Testing for Orthogonality
Determine whether \(\textbf{v}=\langle 2,6,1\rangle\) is orthogonal to \(u = \langle 2,-1,1\rangle\) or \(w = \langle -4, 1, 2\rangle\).
Solution We test for orthogonality by computing the dot products (Figure 12.41): \begin{align*} \textbf{v}\cdot u &= \langle 2,6,1\rangle\cdot \langle 2,-1,1\rangle = 2(2)+6(-1)+1(1)=-1&\quad &\textrm{(not orthogonal)}\\ \textbf{v}\cdot w &= \langle 2,6,1\rangle\cdot \langle -4,1, 2\rangle = 2(-4)+6(1)+1(2) =0&\quad &\textrm{(orthogonal)} \end{align*}
681
EXAMPLE 4 Testing for Obtuseness
Determine whether the angles between the vector \(\textbf{v}=\langle 3,1,-2\rangle\) and the vectors \(u = \big\langle \frac12,\frac12,5\big\rangle\) and \(w = \langle 4,-3,0\rangle\) are obtuse.
Solution By definition, the angle \(\theta\) between \(\textbf{v}\) and \(u\) is obtuse if \(\frac{\pi}2 \lt \theta \le \pi\), and this is the case if \(\cos\theta \lt 0\). Since \(\textbf{v}\cdot u = \parallel{v}\parallel\,\parallel{u}\parallel\cos\parallel\theta\) and the lengths \(\parallel{v}\parallel\) and \(\parallel{u}\parallel\) are positive, we see that \(\cos \theta\) is negative if and only if \(\textbf{v} \cdot u\) is negative. Thus, \[ \boxed{\textrm{The angle \(\theta\) between \(\textbf{v}\) and \(u\) is obtuse if \(\textbf{v}\cdot u \lt 0\).}} \]
We have \begin{align*} \textbf{v}\cdot u &= \langle 3,1,-2\rangle\cdot \langle \frac12,\frac12,5 \rangle = \frac32+\frac12-10 =-8 \lt 0 &\quad &\textrm{(angle is obtuse)}\\ \textbf{v}\cdot w &= \langle 3,1,-2\rangle \cdot \langle 4, -3, 0\rangle = 12-3+0 = 9 \gt 0&\quad &\textrm{(angle is acute)} \end{align*}
EXAMPLE 5 Using the Distributive Law
Calculate the dot product \(\textbf{v}\cdot w\), where \(\textbf{v}=4i-3j\) and \(w= i+2j+k\).
Solution Use the Distributive Law and the orthogonality of \(i\), \(j\), and \(k\): \begin{align*} \textbf{v}\cdot w &= (4i-3j)\cdot ( i+2j+k)\\& = 4i\cdot ( i+2j+k) - 3j\cdot ( i+2j+k)\\ &= 4i\cdot i - 3j\cdot (2j) =4 -6=-2 \end{align*}
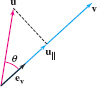
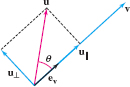
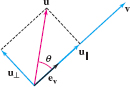
Another important use of the dot product is in finding the projection \(u_{||}\) of a vector \(u\) along a nonzero vector \(\textbf{v}\). By definition, \(u_{||}\) is the vector obtained by dropping a perpendicular from \(u\) to the line through \(\textbf{v}\) as in Figure 12.42 and Figure 12.43. In the next theorem, recall that \({e_v = {v}/{\parallel{v}\parallel}}\) is the unit vector in the direction of \(\textbf{v}\).
THEOREM 3 Projection
Assume \(\textbf{v} \ne v\). The projection of \(u\) along \(\textbf{v}\) is the vector \begin{equation} \label{14.dotprod.dotproj} \boxed{ u_{||} = (u\cdot e_v)e_v \quad\textrm{or}\quad u_{||} = \left(\frac{u\cdot v}{v\cdot v}\right)v } \end{equation}
The scalar \({u\cdot e_v}\) is called the component of \(u\) along \(\textbf{v}\).
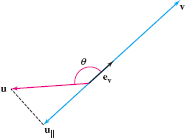
Proof
Referring to Figure 12.42 and Figure 12.43, we see by trigonometry that \(u_{||}\) has length \({\parallel{u}\parallel|\cos\theta|}\). If \(\theta\) is acute, then \(u_{||}\) is a positive multiple of \(e_v\) and thus \(u_{||} = (\parallel{u}\parallel\cos\theta)e_v\) since \(\cos\theta \lt 0\). Similarly, if \(\theta\) is obtuse, then \(u_{||}\) is a negative multiple of \(e_v\) and \(u_{||} = (\parallel{u}\parallel\cos\theta)e_v\) since \(\cos\theta \lt 0\). The first formula for \(u_{||}\) now follows because \({u\cdot e_v = \parallel{u}\parallel\parallel{e_v}\parallel\cos\theta = \parallel{u}\parallel \cos\theta}\).
The second equality in Eq.(4) follows from the computation: \begin{align*} u_{||} &= (u\cdot e_v)e_v = \left(u\cdot \frac{v}{\parallel{v}\parallel}\right)\frac{v}{\parallel{v}\parallel}\\ & = \left(\frac{u\cdot \textbf{v}}{\parallel{v}\parallel^2}\right)v = \left(\frac{u\cdot v}{v\cdot v}\right)v \end{align*}
682
EXAMPLE 6
Find the projection of \(u = \langle 5,1,-3\rangle\) along \(\textbf{v} = \langle 4,4,2\rangle\).
Solution It is convenient to use the second formula in Eq.(4): \begin{gather*} u\cdot v = \langle 5,1,-3\rangle \cdot \langle 4,4,2\rangle= 20+4-6=18,\qquad \textbf{v}\cdot v = 4^2+4^2+2^2 = 36\\ u_{||} = \left(\frac{u\cdot v}{v\cdot v}\right)\,v = \left(\frac{18}{36}\right)\,\langle 4,4,2\rangle = \langle 2,2,1\rangle \end{gather*}
We show now that if \(\textbf{v}\ne v\), then every vector \(u\) can be written as the sum of the projection \({u_{||}}\) and a vector \({u_{\perp}}\) that is orthogonal to \(\textbf{v}\) (see Figure 12.44). In fact, if we set \( u_{\perp} = u-u_{||} \)
then we have \begin{equation}\label{13.5.decompo} \boxed{ u = u_{||}+u_{\perp} } \end{equation}
Eq.(5) is called the decomposition of \(u\) with respect to \(\textbf{v}\). We must verify, however, that \(u_{\perp}\) is orthogonal to \(\textbf{v}\). We do this by showing that the dot product is zero: \[ u_{\perp} \cdot v = (u-u_{||})\cdot v = (u-\left(\frac{u\cdot v}{v\cdot v}\right)v)\cdot v = u\cdot v- \left(\frac{u\cdot v}{v\cdot v}\right)(v\cdot v) = 0 \]
EXAMPLE 7
Find the decomposition of \(u = \langle 5,1,-3\rangle\) with respect to \(\textbf{v} = \langle 4,4,2\rangle\).
Solution In Example 6 we showed that \(u_{||} = \langle 2,2,1\rangle\). The orthogonal vector is \[ u_{\perp} = u - u_{||} = \langle 5,1,-3\rangle - \langle 2,2,1\rangle = \langle 3,-1,-4\rangle\]
The decomposition of \(u\) with respect to \(\textbf{v}\) is \[ u = \langle 5,1,-3\rangle = u_{||}+u_{\perp} = \underbrace{\langle 2,2,1\rangle}_{\textrm{Projection along \(\textbf{v}\)}} + \underbrace{\langle 3,-1,-4\rangle}_{\textrm{Orthogonal to \(\textbf{v}\)}} \]
The decomposition into parallel and orthogonal vectors is useful in many applications.
EXAMPLE 8
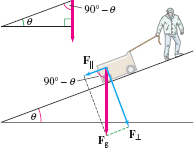
What is the minimum force you must apply to pull a 20-kg wagon up a frictionless ramp inclined at an angle \(\theta = 15^\circ\)?
Solution Let \(F_{\textrm{g}}\) be the force on the wagon due to gravity. It has magnitude \(20g\) newtons with \(g = 9.8\). Referring to Figure 12.45, we decompose \(F_{\textrm{g}}\) as a sum \[ F_{\textrm{g}} = F_{||} + F_{\perp} \]
where \(F_{||}\) is the projection along the ramp and \(F_\perp\) is the “normal force” orthogonal to the ramp. The normal force \(F_\perp\) is canceled by the ramp pushing back against the wagon in the normal direction, and thus (because there is no friction), you need only pull against \(F_{||}\).
Notice that the angle between \(F_{\mathrm{g}}\) and the ramp is the complementary angle \(90^\circ-\theta\). Since \(F_{||}\) is parallel to the ramp, the angle between \(F_{\textrm{g}}\) and \(F_{||}\) is also \(90^\circ-\theta\), or \(75^\circ\), and \[ \parallel{F_{||}}\parallel = \parallel{F_{\textrm{g}}}\parallel\cos(75^\circ) \approx 20(9.8) (0.26) \approx 51 \textrm{N} \]
Since gravity pulls the wagon down the ramp with a \(51\)-newton force, it takes a minimum force of 51 newtons to pull the wagon up the ramp.
683
GRAPHICAL INSIGHT
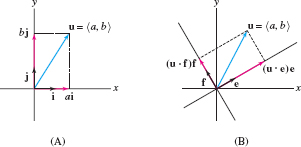
It seems that we are using the term “component” in two ways. We say that a vector \(u = \langle a,b\rangle\) has components \(a\) and \(b\). On the other hand, \(u\cdot e\) is called the component of \(u\) along the unit vector \( e\).
In fact, these two notions of component are not different. The components \(a\) and \(b\) are the dot products of \(u\) with the standard unit vectors: \begin{align*} u\cdot i &= \langle a,b\rangle\cdot \langle 1,0\rangle = a\\ u\cdot j &= \langle a,b\rangle\cdot \langle 0,1\rangle = b \end{align*}
and we have the decomposition [Figure 12.46] \( u = a i+b j \)
But any two orthogonal unit vectors \( e\) and \( f\) give rise to a rotated coordinate system, and we see in Figure 12.46 that \( u = (u\cdot e)e + (u\cdot f) f \)
In other words, \(u\cdot e\) and \(u\cdot f\) really are the components when we express \(u\) relative to the rotated system.
12.4.1 Summary
- The dot product of \(\textbf{v}=\langle a_1, b_1, c_1\rangle\) and \(w=\langle a_2, b_2, c_2\rangle\) is \[ \textbf{v}\cdot w= a_1a_2+b_1b_2+c_1c_2 \]
- Basic Properties:
- – Commutativity: \(\textbf{v}\cdot w = w\cdot v\)
- – Pulling out scalars:\(\quad {(\lambda v)\cdot w=v\cdot (\lambda w)=\lambda(v\cdot w)}\)
- – Distributive Law:\(\quad \begin{array}[t]{lcl} u\cdot (v+w) & {}={} & u\cdot v+u\cdot w \\ (v+w)\cdot u & =& v\cdot u+w\cdot u \\ \end{array}\)
- – \({\boxed{v\cdot v = \parallel{v}^2}}\)
- – \(\boxed{ \textbf{v}\cdot w = \parallel{v}\,\parallel{w}\cos\theta} \quad\) where \(\theta\) is the angle between \(\textbf{v}\) and \(\textbf{w}\).
- By convention, the angle \(\theta\) is chosen to satisfy \(0\le\theta\le \pi\).
- Test for orthogonality: \(\textbf{v}\perp w\) if and only if
\(\textbf{v}\cdot w = 0\).
684
- The angle between \(\textbf{v}\) and \(\textbf{w}\) is acute if \(\textbf{v}\cdot w \gt 0\) and obtuse if \(\textbf{v}\cdot w \lt 0\).
- Assume \(\textbf{v}\ne v\). Every vector \(u\) has a decomposition \(u=u_{||}+u_{\perp}\), where \(u_{||}\) is parallel to \(\textbf{v}\), and \(u_{\perp}\) is orthogonal to \(\textbf{v}\) (see Figure 12.47). The vector \(u_{||}\) is called the projection of \(u\) along \(\textbf{v}\).
- Let \({e_v=\frac{v}{\parallel{v}}}\). Then \[ \boxed{u_{||} = (u\cdot e_v)e_v = \left(\frac{u\cdot v}{v\cdot v}\right)v ,\qquad u_{\perp} = u - u_{||} } \]
- The coefficient \(u\cdot e_{v}\) is called the component of \(u\) along \(\textbf{v}\): \[ \boxed{\textrm{Component of \(u\) along \(\textbf{v}\)} = u\cdot e_v = \parallel{u}\parallel\cos\theta } \]