12.6 Planes in Three-Space
A linear equation \(ax+by=c\) in two variables defines a line in \(\textbf{R}^2\). In this section we show that a linear equation \(ax+by+cz=d\) in three variables defines a plane in \(\textbf{R}^3\).
Consider a plane \(\mathcal P\) that passes through a point \(P_0 = (x_0,y_0,z_0)\). We can determine \(\mathcal P\) completely by specifying a nonzero vector \(n = \langle a,b,c\rangle\) that is orthogonal to \(\mathcal P\). Such a vector is called a normal vector. Basing \(n\) at \(P_0\) as in Figure 12.62, we see that a point \(P = (x, y, z)\) lies on \(\mathcal P\) precisely when \(\overrightarrow{P_0P}\) is orthogonal to \(n\). Therefore, \(P\) lies on the plane if \begin{equation} \label{14.planes.oneq} n\cdot \overrightarrow{P_0P} = 0 \end{equation}
Note
The term “normal” is another word for “orthogonal” or “perpendicular.”
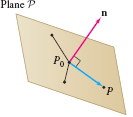
In components, \({ \overrightarrow{P_0P} = \langle x - x_0,y - y_0,z - z_0\rangle}\), so Eq.(1) reads \[ \langle a,b,c\rangle \cdot \langle x - x_0,y - y_0,z - z_0\rangle =0 \]
This gives us the following equation for the plane: \[ a(x-x_0) + b(y-y_0) + c(z-z_0) = 0 \]
This can also be written \begin{equation}\label{14.planes.oneq2} ax +by +cz = ax_0 +by_0 +cz_0\qquad\textrm{or}\qquad n\cdot \overrightarrow{OP} = n\cdot \overrightarrow{OP_0} \end{equation}
When we set \(d= ax_0+by_0+cz_0 = n\cdot \overrightarrow{OP_0}\), Eq.(2) becomes \({n\cdot \langle x, y, z\rangle = d}\), or \[ ax+by+cz = d \]
THEOREM 1 Equation of a Plane
Plane through \(P_0=(x_0,y_0,z_0)\) with normal vector \(n=\langle a,b,c\rangle\): \begin{align}\label{14.planes.veceq} &\textbf{Vector form:}&\quad\quad n\cdot \overrightarrow{OP} = d\quad\textrm{or}\quad n\cdot \langle x, y, z\rangle &= d\\ \label{14.planes.scaleq} &\textbf{Scalar forms:}\quad\quad&\quad a(x-x_0)+b(y-y_0)+c(z-z_0)&=0\\ \label{14.planes.scaleq2} & \quad\quad&\quad ax+by+cz&=d \end{align}
where \(d = n\cdot \langle x_0,y_0,z_0\rangle= ax_0+by_0+cz_0\).
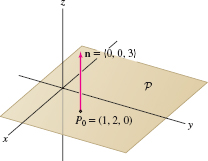
To show how this works in a simple case, consider the plane \(\mathcal P\) through \(P_0=(1,2,0)\) with normal vector \(n=\langle 0,0,3\rangle\) (Figure 12.63). Because \(n\) points in the \(z\)-direction, \(\mathcal P\) must be parallel to the \(xy\)-plane. On the other hand, \(P_0\) lies on the \(xy\)-plane, so \(\mathcal P\) must be the \(xy\)-plane itself. This is precisely what Eq.(3) gives us: \begin{align*} n\cdot \langle x,y,z\rangle &= n\cdot \langle 1,2,0\rangle\\ \langle 0,0,3\rangle\cdot \langle x,y,z\rangle &= \langle 0,0,3\rangle\cdot \langle 1,2,0\rangle\\ 3z &= 0\quad\hbox{or}\quad z = 0 \end{align*}
In other words, \(\mathcal P\) has equation \(z=0\), so \(\mathcal P\) is the \(xy\)-plane.
700
EXAMPLE 1
Find an equation of the plane through \(P_0=(3,1,0)\) with normal vector \(n=\langle 3,2,-5\rangle\).
Solution Using Eq.(4), we obtain \[ 3(x-3)+2(y-1)-5z=0 \]
Alternatively, we can compute \[ d = n\cdot \overrightarrow{OP_0} = \langle 3,2,-5\rangle\cdot \langle 3,1,0\rangle = 11 \] and write the equation as \(\langle 3,2,-5\rangle \cdot \langle x, y, z\rangle = 11\), or \({ 3x+2y-5z = 11}\).
CONCEPTUAL INSIGHT
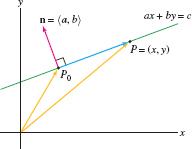
Keep in mind that the components of a normal vector are “lurking” inside the equation \(ax+by+cz=d\), because \(n = \langle a, b, c\rangle\). The same is true for lines in \(\textbf{R}^2\). The line \(ax+by=c\) in Figure 12.64 has normal vector \(n = \langle a, b\rangle\) because the line has slope \(-a/b\) and the vector \(n\) has slope \(b/a\) (lines are orthogonal if the product of their slopes is \(-1)\).
Note that if \(n\) is normal to a plane \(\mathcal P\), then so is every nonzero scalar multiple \(\lambda n\). When we use \(\lambda n\) instead of \(n\), the resulting equation for \(\mathcal P\) changes by a factor of \(\lambda\). For example, the following two equations define the same plane: \[ x+y+z =1,\qquad 4x+4y+4z = 4 \]
The first equation uses the normal \(\langle 1,1,1\rangle\), and the second uses the normal \(\langle 4,4,4\rangle\).
On the other hand, two planes \(\mathcal P\) and \(\mathcal P'\) are parallel if they have a common normal vector. The following planes are parallel because each is normal to \(n=\langle 1,1,1\rangle\): \[ x+y+z =1,\qquad x+ y+ z = 2,\qquad 4x+ 4y+ 4z = 7 \]
In general, a family of parallel planes is obtained by choosing a normal vector \(n=\langle a,b,c\rangle\) and varying the constant \(d\) in the equation \[ ax+by+cz=d \]
The unique plane in this family through the origin has equation \(ax+by+cz= 0\).
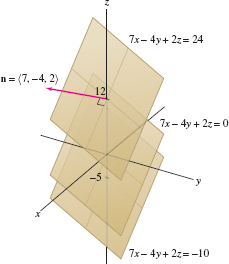
EXAMPLE 2 Parallel Planes
Let \(\mathcal P\) have equation \(7x- 4y+ 2z=-10\). Find an equation of the plane parallel to \(\mathcal P\) passing through
- (a) The origin.
- (b) \(Q = (2,-1,3)\).
Solution The planes parallel to \(\mathcal P\) have an equation of the form (Figure 12.65) \begin{equation} \label{14.planes.parall} 7x - 4y + 2z = d \end{equation}
- (a) For \(d=0\), we get the plane through the origin: \(7x - 4y+2z=0\).
- (b) The point \(Q = (2,-1,3)\) satisfies Eq.(6) with \[ d=7(2) -4(-1)+2(3) = 24 \]
Therefore, the plane parallel to \(\mathcal P\) through \(Q\) has equation \(7x - 4y + 2z = 24\).
701
Points that lie on a line are called collinear. If we are given three points \(P\), \(Q\), and \(R\) that are not collinear, then there is just one plane passing through \(P\), \(Q\), and \(R\) (Figure 12.66). The next example shows how to find an equation of this plane.
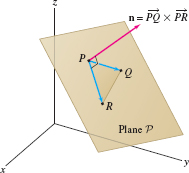
EXAMPLE 3 The Plane Determined by Three Points
Find an equation of the plane \(plane\) determined by the points \[ P = (1,0,-1),\qquad Q = (2,2,1),\qquad R = (4,1,2) \]
Solution
Step 1. Find a normal vector.
The vectors \(\overrightarrow{PQ}\) and \(\overrightarrow{PR}\) lie in the plane \(\mathcal P\), so their cross product is normal to \(\mathcal P\): \begin{align*} \overrightarrow{PQ} &= \langle 2,2,1\rangle - \langle 1,0,-1\rangle = \langle 1,2,2\rangle\\ \overrightarrow{PR} &= \langle 4,1,2\rangle - \langle 1,0,-1\rangle = \langle 3,1,3\rangle\\ n &= \overrightarrow{PQ}\times \overrightarrow{PR} = \left| \begin{array}{ccc} i & j& k \\ 1& 2&2 \\ 3 & 1&3 \\ \end{array} \right| = 4i +3j-5 k=\langle 4,3,-5\rangle \end{align*}
By Eq.(5), \(\mathcal P\) has equation \(4x +3y -5z=d\) for some \(d\).
Step 2. Choose a point on the plane and compute \(d\).
Now choose any one of the three points—say, \(P=(1,0,-1)\)—and comput \[ d = n\cdot \overrightarrow{OP} = \langle 4,3,-5\rangle\cdot \langle 1,0,-1\rangle = 9 \]
We conclude that \(\mathcal P\) has equation \(4x+3y-5z=9\).
Note
In Example 3, we could just as well have used the vectors \(\overrightarrow{QP}\) and \(\overrightarrow{QR}\) (or \(\overrightarrow{RP}\) and \(\overrightarrow{RQ})\) to find a normal vector \(n\).
CAUTION
When you find a normal vector to the plane containing points \(P, Q, R\), be sure to compute a cross product such as \(\overrightarrow{PQ}\times \overrightarrow{PR}\). A common mistake is to use a cross product such as \(\overrightarrow{OP}\times \overrightarrow{OQ}\) or \(\overrightarrow{OP}\times \overrightarrow{OR}\), which need not be normal to the plane.
EXAMPLE 4 Intersection of a Plane and a Line
Find the point \(P\) where the plane \(3x-9y+2z=7\) and the line \(r(t)=\langle 1,2,1\rangle+t\langle -2,0,1 \rangle\) intersect.
Solution The line has parametric equations \[ x = 1-2t,\qquad y = 2,\qquad z = 1+t \]
Substitute in the equation of the plane and solve for \(t\): \begin{align*} 3x-9y+2z&= 7\\ 3x-9y+2z = 3(1-2t)-9(2)+ 2(1+t)&= 7 -4t-13&=7\qquad\hbox{(simplify)} \end{align*}
Simplification yields \(-4t-13=7\) or \(t=-5\). Therefore, \(P\) has coordinates \[ x=1-2(-5)=11,\qquad y = 2,\qquad z = 1+(-5)=-4 \]
The plane and line intersect at the point \(P = (11,2,-4)\).
The intersection of a plane \(\mathcal P\) with a coordinate plane or a plane parallel to a coordinate plane is called a trace. The trace is a line unless \(\mathcal P\) is parallel to the coordinate plane (in which case the trace is empty or is \(\mathcal P\) itself).
702
EXAMPLE 5 Traces of the Plane
Find the traces of the plane \(-2x+3y+z=6\) in the coordinate planes.
Solution We obtain the trace in the \(xy\)-plane by setting \(z=0\) in the equation of the plane. Thus, the trace is the line \(-2x+3y =6\) in the \(xy\)-plane (Figure 12.67).
Similarly, the trace in the \(xz\)-plane is obtained by setting \(y=0\), which gives the line \(-2x+z=6\) in the \(xz\)-plane. Finally, the trace in the \(yz\)-plane is \(3y+z=6\).

12.6.1 Summary
- Equation of plane through \(P_0=(x_0, y_0,z_0)\) with normal vector \(n = \langle a,b,c\rangle\): \begin{align*} &\textbf{Vector form:}& \quad\quad n\cdot \overrightarrow{OP} = d\quad\textrm{or}\quad n\cdot \langle x, y, z\rangle &= d\\ &\textbf{Scalar forms:}\quad\quad&\quad a(x-x_0)+b(y-y_0)+c(z-z_0)&=0\\ & \quad\quad&\quad ax+by+cz&=d \end{align*} where \(d = n\cdot \langle x_0, y_0,z_0\rangle = ax_0+by_0+cz_0\).
- The family of parallel planes with given normal vector \(n=\langle a,b,c\rangle\) consists of all planes with equation \(ax+by+cz=d\) for some \(d\).
- The plane through three points \(P\),
\(Q\), \(R\) that are not collinear:
- – \(n = \overrightarrow{PQ}\times \overrightarrow{PR}\)
- – \(d = n\cdot \langle x_0,y_0,z_0\rangle\), where \(P=(x_0,y_0,z_0)\)
- The intersection of a plane \(\mathcal P\) with a coordinate plane or a plane parallel to a coordinate plane is called a trace. The trace in the \(yz\)-plane is obtained by setting \(x=0\) in the equation of the plane (and similarly for the traces in the \(xz\)- and \(xy\)-planes).