1.6 Exponential and Logarithmic Functions

An exponential function is a function of the form \(f(x) = b^{x}\), where \(b > 0 \) and \(b \neq 1\). The number \(b\) is called the base. Some examples are \(2^{x}\), \((1.4)^{x}\), and \(10^{x}\). The case \(b = 1\) is excluded because \(f(x) = 1^{x}\) is a constant function. Calculators give good decimal approximations to values of exponential functions:
\[ 2^4=16,\quad 3^{-3}=0.125,\quad (1.4)^{0.8}\approx1.309,\quad 10^{4.6}\approx39,810.717 \]
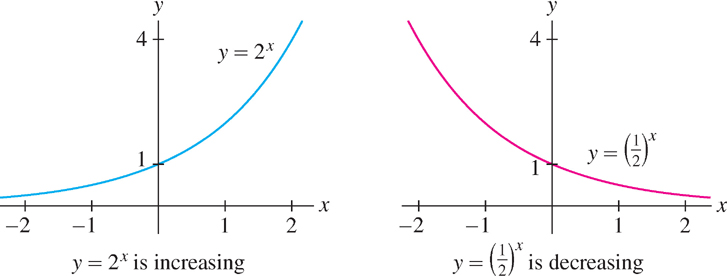
Three properties of exponential functions should be singled out from the start (see Figure 1.76 for the case \(b = 2\)):
- Exponential functions are positive: \(b^{x} > 0\) for all \(x\).
- The range of \(f(x) = b^{x}\) is the set of all positive real numbers.
- \(f(x) = b^{x}\) is increasing if \(b > 1\) and decreasing if \(0 < b < 1\).
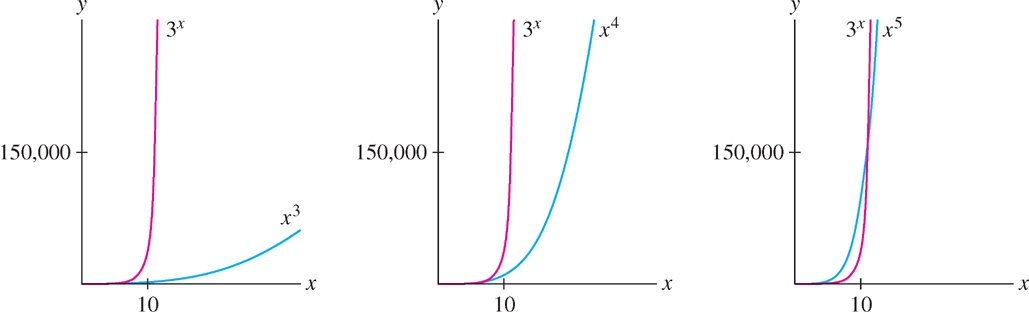
If \(b > 1\), the exponential function \(f(x) = b^{x}\) is not merely increasing but is, in a certain sense, rapidly increasing. Although the term “rapid increase” is perhaps subjective, the following precise statement is true: \(f(x) = b^{x}\) increases more rapidly than the power function \(x^{n}\) for all \(n\) (we will prove this in Section 4.5). For example, Figure 1.77 shows that \(f(x) = 3^{x}\) eventually overtakes and increases faster than the power functions \(x^{3}\), \(x^{4}\), and \(x^{5}\). Table 1.8 compares \(3^{x}\) and \(x^{5}\).
| \(x\) | \(x^{5}\) | \(3^{x}\) |
| \(1\) | \(1\) | \(3\) |
| \(5\) | \(3125\) | \(243\) |
| \(10\) | \(100,000\) | \(59,049\) |
| \(15\) | \(759,375\) | \(14,348,907\) |
| \(25\) | \(9,765,625\) | \(847,288,609,443\) |
We now review the laws of exponents. The most important law is
\[ \boxed{b^xb^y=b^{x+y}} \]
In other words, under multiplication, the exponents add, provided that the bases are the same. This law does not apply to a product such as \(3^{2} \cdot 5^{4}\).
44
Laws of Exponents (\(b > 0\;\))
Be sure you are familiar with the laws of exponents. They are used throughout this text.
\[ \begin{array}{lll} \hline &\quad\text{Rule}&\quad\text{Example}\\ \hline \text{Exponent zero}&\quad b^0 = 1&\\[5pt] \text{Products}&\quad b^xb^y=b^{x+y}& \quad2^5\cdot2^3=2^{5+3}=2^8\\[5pt] \text{Quotients}&\quad\frac{b^x}{b^y}=b^{x-y}& \quad\frac{4^7}{4^2}=4^{7-2}=4^5\\[5pt] \text{Negative exponents}&\quad b^{-x}=\frac{1}{b^x}& \quad3^{-4}=\frac{1}{3^4}=\frac{1}{81}\\[5pt] \text{Power to a power}&\quad(b^x)^y=b^{xy}& \quad(3^2)^4=3^{2(4)}=3^8\\[5pt] \text{Roots}&\quad b^{\frac{1}{n}}\sqrt[n]{b}& \quad5^{\frac{1}{2}}=\sqrt{5} \end{array} \]
EXAMPLE 1
Rewrite as a whole number or fraction:
(a) \(16^{-\frac{1}{2}}\)
(b) \(27^{\frac{2}{3}}\)
(c) \(4^{16} \cdot 4^{-18}\)
(d) \(\frac{9^3}{3^7}\)
Solution
(a) \(16^{-\frac{1}{2}}=\frac{1}{16^{1/2}}=\frac{1}{\sqrt{16}}=\frac{1}{4}\).
(b) \(27^{\frac{2}{3}} = (27^{\frac{1}{3}})^{2} = 3^{2} = 9\).
(c) \(4^{16} \cdot 4^{-18}=4^{-2}=\frac{1}{4^2}=\frac{1}{16}\).
(d) \(\frac{9^3}{3^7} = \frac{(3^2)^3}{3^7}=\frac{3^6}{3^7}=3^{-1}=\frac{1}{3}\).
In the next example, we use the fact that \(f(x) = b^{x}\) is one-to-one. In other words, if \(b^{x} = b^{y}\), then \(x = y\).
EXAMPLE 2
Solve for the unknown:
(a) \(2^{3x+1} = 2^{5}\)
(b) \(b^{3} = 5^{6}\)
(c) \(7^{t+1} = \left(\frac{1}{7}\right)^{2t}\)
Solution
(a) If \(2^{3x+1} = 2^{5}\), then \(3x + 1 = 5\) and thus \(x=\frac{4}{3}\).
(b) Raise both sides of \(b^{3} = 5^{6}\) to the \(\frac{1}{3}\) power. By the “power to a power” rule, \[ b=(b^3)^{\frac{1}{3}}=(5^6)^{\frac{1}{3}}=5^{\frac{6}{3}}=5^2=25 \]
(c) Since \(\frac{1}{7}=7^{-1}\), the right-hand side of the equation is \((\frac{1}{7})^{2t}=(7^{-1})^{2t}=7^{-2t}\). The equation becomes \(7^{t+1} = 7^{-2t}\). Therefore, \(t + 1 = -2t\), or \(t=-\frac{1}{3}\).
45
1.6.1 The Number e
Although written references to the number \(\pi\) go back more than 4000 years, mathematicians first became aware of the special role played by \(e\) in the seventeenth century. The notation \(e\) was introduced by Leonhard Euler, who discovered many fundamental properties of this important number.
In Chapter 3, we will use calculus to study exponential functions. One of the surprising insights of calculus is that the most convenient or “natural” base for an exponential function is not \(b = 10\) or \(b = 2\), as one might think at first, but rather a certain irrational number, denoted by \(e\), whose value is approximately \(e \approx 2.718\). A calculator is used to evaluate specific values of \(f(x) = e^{x}\). For example,
\[ e^3\approx20.0855,\quad e^{-\frac{1}{4}}\approx0.7788 \]
In calculus, when we speak of the exponential function, it is understood that the base is \(e\). Another common notation for the exponential function \(e^{x}\) is \(\exp(x)\).
How is \(e\) defined? There are many different definitions, but they all rely on the calculus concept of a limit. We shall discuss one way of defining \(e\) in Section 3.2. Another definition is described in Example 4 of Section 1.7. For now, we mention the following two graphical descriptions.
- Using Figure 1.78(A): Among all exponential functions \(y = b^{x}\), \(b = e\) is the unique base for which the slope of the tangent line to the graph at \((0, 1)\) is equal to 1.
- Using Figure 1.78(B): The number \(e\) is the unique number such that the area of the region under the hyperbola \(y = \frac{1}{x}\) for \(1 \leq x \leq e\) is equal to \(1\).
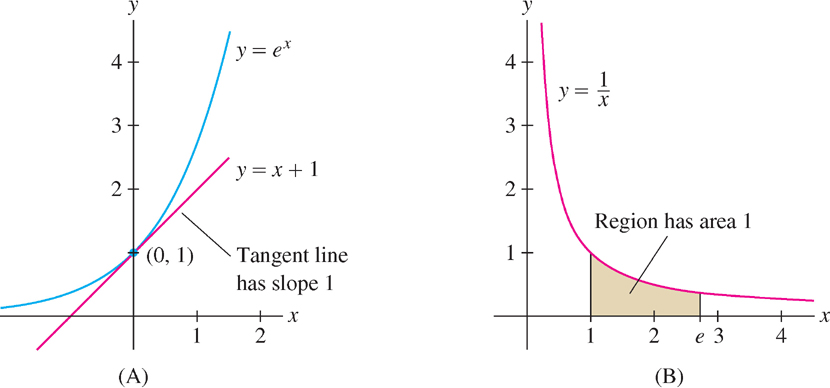
From these descriptions it is not clear why \(e\) is important. As we will learn, however, the exponential function \(e^{x}\) plays a fundamental role because it behaves in a particularly simple way with respect to the basic operations of calculus: differentiation and integration.
1.6.2 Logarithms

Logarithmic functions are inverses of exponential functions. More precisely, if \(b > 0\) and \(b \neq 1\), then the logarithm to the base b, denoted \(\log_{b} x\), is the inverse of \(f(x) = b^{x}\). By definition, \(y = \log_{b} x\) if \(b^{y} = x\), so we have
\[ \boxed{b^{\log_bx}=x\quad\text{and}\quad\log_b(b^x)=x} \]
In other words, \(\log_{b} x\) is the number to which \(b\) must be raised in order to get \(x\). For example,
\[ \begin{array}{rcl} \log_28=3&\text{because}&2^3=8\\ \log_{10}(1)=0&\text{because}&10^0=1\\ \log_3\left(\frac{1}{9}\right)=-2&\text{because}& 3^{-2}=\frac{1}{3^2}=\frac{1}{9} \end{array} \]
46
The logarithm to the base \(e\), denoted \(\ln x\), plays a special role and is called the natural logarithm. We use a calculator to evaluate logarithms numerically. For example,
\[ \ln17\approx2.83321\quad\text{because}\quad e^{2.83321}\approx17 \]
Recall that the domain of \(b^{x}\) is \(\mathbb{R}\) and its range is the set of positive real numbers \(\{x : x > 0\}\). Since the domain and range are reversed in the inverse function,
- The domain of \(\log_{b} x\) is \(\{x: x > 0\}\).
- The range of \(\log_{b} x\) is the set of all real numbers \(\mathbb{R}\).
In this text, the natural logarithm is denoted \(\ln x\). Other common notations are \(\log x\) and \(\text{Log}\,x\).
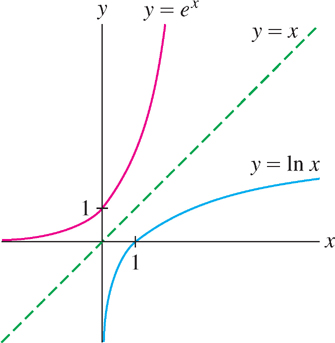
If \(b \gt 1\), then \(\log_{b} x\) is positive for \(x \gt 1\) and negative for \(0 \lt x \lt 1\). Figure 1.79 illustrates these facts for the base \(b = e\). Keep in mind that the logarithm of a negative number does not exist. For example,\(\log_{10}(-2)\) does not exist because \(10^{y} = -2\) has no solution.
For each law of exponents, there is a corresponding law for logarithms. The rule \(b^{x+y} = b^{x}b^{y}\) corresponds to the rule
\[ \boxed{\log_b(xy)=\log_bx+\log_by} \]
In words: The log of a product is the sum of the logs. To verify this rule, observe that
\begin{align*} b^{\log_b(xy)}=xy&=b^{\log_bx}\cdot b^{\log_by}\\ &=b^{\log_bx+\log_by} \end{align*}
The exponents \(\log_{b}(xy)\) and \(\log_{b} x + \log_{b} y\) are equal as claimed because \(f(x) = b^{x}\) is one-to-one. The remaining logarithm laws are collected in the following table.
Laws of Logarithms
\[ \begin{array}{lll} \hline &\text{Law}&\text{Example}\\ \hline \text{Log of }1\quad&\log_b(1)=0\quad&\\[5pt] \text{Log of }b\quad&\log_b(b)=1\quad&\\[5pt] \text{Products}\quad&\log_b(xy)=\log_bx+\log_by \quad&\log_5(2\cdot3)=\log_52+\log_53\\[5pt] \text{Quotients}\quad& \log_b\left(\frac{x}{y}\right)=\log_bx-\log_by\quad& \log_2\left(\frac{3}{7}\right)=\log_23-\log_27\\[5pt] \text{Reciprocals}\quad& \log_b\left(\frac{1}{x}\right)=-\log_bx\quad& \log_2\left(\frac{1}{7}\right)=-\log_27\\[5pt] \text{Powers (any \(n\))}\quad& \log_b(x^n)=n\log_bx\quad& \log_{10}(8^2)=2\cdot\log_{10}8 \end{array} \]
We note also that all logarithmic functions are proportional. More precisely, the following change-of-base formula holds (see Exercise 49):
\[ \boxed{\log_bx=\dfrac{\log_ax}{\log_ab},\quad\log_bx=\dfrac{\ln x}{\ln b}}\tag{1} \]
47
EXAMPLE 3 Using the Logarithm Laws
Evaluate:
(a) \(\log_69+\log_64\)
(b) \(\ln\left(\frac{1}{\sqrt{e}}\right)\)
(c) \(10\log_b(b^3)-4\log_4(\sqrt{b})\)
Solution
(a) \(\log_69+\log_64=\log_6(9\cdot4)=\log_6(35)=\log_6(6^2)=2\)
(b) \(\ln\left(\frac{1}{\sqrt{e}}\right)=\ln(e^{-\frac{1}{2}})=-\frac{1}{2}\ln(e)=-\frac{1}{2}\)
(c) \(10\log_b(b^3)-4\log_4(\sqrt{b})=10(3)-4\log_b(b^{\frac{1}{2}})=30 - 4\left(\frac{1}{2}\right)=28\)
EXAMPLE 4 Solving an Exponential Equation
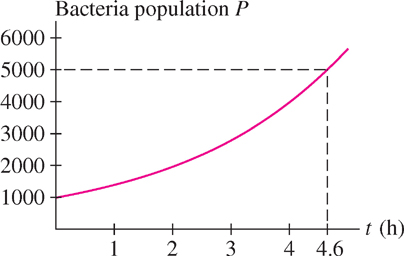
The bacteria population in a bottle at time \(t\) (in hours) has size \(P(t)=1000e^{0.35t}\). After how many hours will there be \(5000\) bacteria?
Solution We must solve \(P(t)=1000e^{0.35t}=5000\) for \(t\) (Figure 1.80):
\begin{align*} e^{0.35t}&=\frac{5000}{1000}=5\\ \ln(e^{0.35t})&=\ln5&&\text{(take logarithms of both sides)}\\ 0.35t&=\ln5\approx1.609&&\text{[because \(\ln(e^a)=a\)]}\\ t&\approx\frac{1.609}{0.35}\approx4.6\text{ hours} \end{align*}
1.6.3 Section 1.6 Summary
- \(f(x) = b^{x}\) is the exponential function with base \(b\) (where \(b > 0\) and \(b \neq 1\)).
- \(f(x) = b^{x}\) is increasing if \(b > 1\) and decreasing if \(b < 1\).
- The number \(e \approx 2.718\).
- For \(b > 0\) with \(b \neq 1\), the logarithmic function \(\log_{b} x\) is the inverse of \(b^{x}\); \[ y=\log_bx \Leftrightarrow x=b^{y} \]
- The natural logarithm is the logarithm with base \(e\) and is denoted \(\ln x\).
- Important logarithm laws:
(i) \(\log_{b}(xy) = \log_{b} x + \log_{b} y\)
(ii) \(\log_b\left(\frac{x}{y}\right)=\log_bx-\log_by\)
(iii) \(\log_{b}(x^{n}) = n \log_{b}x\)
(iv) \(\log_{b} 1 = 0\) and \(\log_{b} b = 1\)