2.6 Trigonometric Limits
In our study of the derivative, we will need to evaluate certain limits involving transcendental functions such as sine and cosine. The algebraic techniques of the previous section are often ineffective for such functions, and other tools are required. In this section, we discuss one such tool—the Squeeze Theorem—and use it to evaluate the trigonometric limits needed in Section 3.6.
2.6.1 The Squeeze Theorem
Consider a function \(f(x)\) that is “trapped” between two functions \(l(x)\) and \(u(x)\) on an interval \(I\). In other words, \[l(x)\leq f(x)\leq u(x)\text{ for all }x\in I\]Thus, the graph of \(f(x)\) lies between the graphs of \(l(x)\) and \(u(x)\) (Figure 2.36).
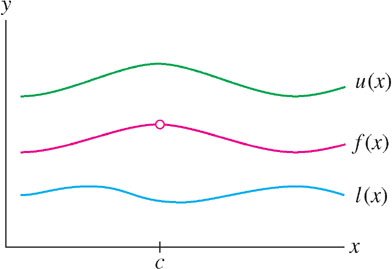
The Squeeze Theorem applies when \(f(x)\) is not just trapped but squeezed at a point \(x=c\) (Figure 2.37). By this we mean that for all \(x\neq c\) in some open interval containing \(c\), \[l(x)\leq f(x)\leq u(x)\text{ and } \lim\limits_{x\rightarrow c} l(x) = \lim\limits_{x\rightarrow c} u(x) = L\]
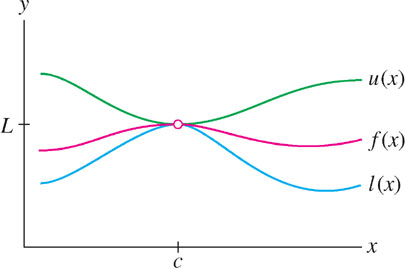
We do not require that \(f(x)\) be defined at \(x=c\), but it is clear graphically that \(f(x)\) must approach the limit \(L\), as stated in the next theorem. See Appendix D for a proof.
96
THEOREM 1 Squeeze Theorem
Assume that for \(x\neq c\) (in some open interval containing \(c\)),\[l(x)\leq f(x)\leq u(x)\text{ and } \lim\limits_{x\rightarrow c} l(x) = \lim\limits_{x\rightarrow c} u(x) = L\]Then \(\lim\limits_{x\rightarrow c} f(x) \) exists and \(\lim\limits_{x\rightarrow c}f(x)=L\).
Example 1
Show that \(\lim\limits_{x\rightarrow 0}x\sin\frac{1}{x} = 0\).
Solution Although \(f(x)=x\sin\frac{1}{x}\) is a product of two functions, we cannot use the Product Law because \(\lim\limits_{x\rightarrow 0}\sin\frac{1}{x}\) does not exist. However, the sine function takes on values between 1 and −1, and therefore \(\left|\sin\frac{1}{x}\right|\leq 1\) for all \(x\neq 0\). Multiplying by \(|x|\), we obtain \(\left|x\sin\frac{1}{x}\right|\) and conclude that (Figure 2.38)\[-|x|\leq x\sin\frac{1}{x}\leq |x|\]

Because\[\lim\limits_{x\rightarrow 0}|x| = 0\quad\text{and}\quad\lim\limits_{x\rightarrow 0}(-|x|) = - \lim\limits_{x\rightarrow 0}|x| = 0\]we can apply the Squeeze Theorem to conclude that \(\lim\limits_{x\rightarrow 0}x\sin\frac{1}{x} = 0\).
In Section 2.6, we found numerical and graphical evidence suggesting that the limit \(\lim\limits_{\theta\rightarrow 0} \frac{\sin\theta}{\theta}\) is equal to 1. The Squeeze Theorem will allow us to prove this fact.
Note that both \(\frac{\sin\theta}{\theta}\) and \(\frac{1-\cos\theta}{\theta}\) are indeterminate at \(\theta=0\), so Theorem 2 cannot be proved by substitution.
THEOREM 2 Important Trigonometric Limits
\[\lim\limits_{\theta\rightarrow 0}\frac{\sin\theta}{\theta} = 1,\quad \lim\limits_{\theta\rightarrow 0}\frac{1 - \cos\theta}{\theta} = 0\]
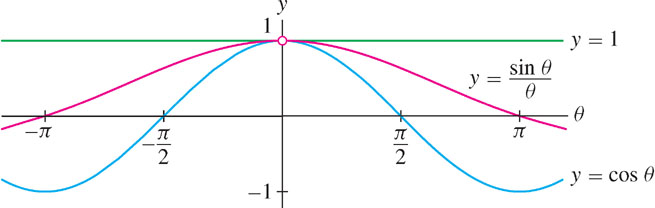
To apply the Squeeze Theorem, we must find functions that squeeze \(\frac{\sin\theta}{\theta}\) at \(\theta=0\). These are provided by the next theorem (Figure 2.39).
THEOREM 3
\[\cos\theta\leq\frac{\sin\theta}{\theta}\leq1 \text{ for all } 0 < \theta < \frac{\pi}{2} \text { and } -\frac{\pi}{2} < \theta < 0\]
97
Proof
Assume that \(0 \lt \theta \lt \frac{\pi}{2}\). Our proof is based on the following relation between the areas in Figure 2.40: \[\text{Area of }\Delta OAB \lt \text{Area of sector } BOA \lt \text{Area of }\Delta OAC\tag{2}\]
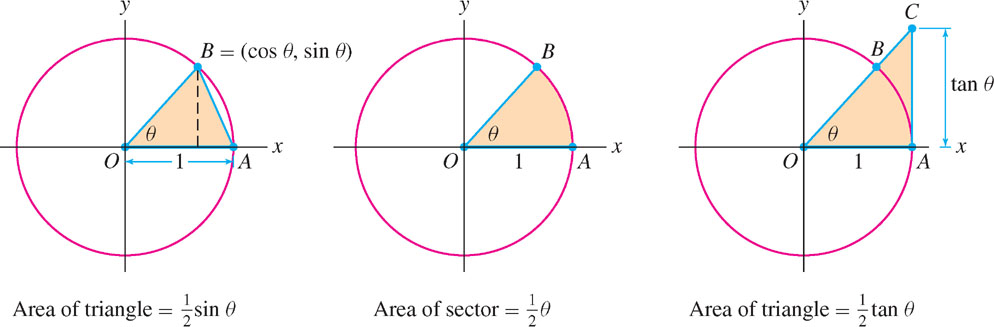
REMINDER Let’s recall why a sector of angle \(\theta\) in a circle of radius \(r\) has area \(\frac{1}{2}r^2\theta\). A sector of angle \(\theta\) represents a fraction \(\frac{\theta}{2\pi}\) of the entire circle. The circle has area \(\pi r^2\) so the sector has area \(\left(\frac{\theta}{2\pi}\right)\pi r^2 = \frac{1}{2}r^2\theta\). In the unit circle (\(r=1\)), the sector has area \(\frac{1}{2}\theta\).
Let’s compute these three areas. First, \(\Delta OAB\) has base 1 and height \(\sin\theta\), so its area is \(\frac{1}{2}\sin\theta\). Next, recall that a sector of angle \(\theta\) has area \(\frac{1}{2}\theta\). Finally, to compute the area of \(\Delta OAC\), we observe that \[\tan\theta = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{AC}{OA} = \frac{AC}{1} = AC\]
Thus, \(\Delta OAC\) has base 1, height \(\tan\theta\), and area \(\frac{1}{2}\tan\theta\). We have shown, therefore, that \[\underbrace{\frac{1}{2}\sin\theta}_{\text{Area of }\Delta OAB}\leq\underbrace{\frac{1}{2}\theta}_{\text{Area of Sector}}\leq\underbrace{\frac{1}{2}\frac{\sin\theta}{\cos\theta}}_{\text{Area of }\Delta OAC}\tag{3}\]
Note: Our proof of Theorem 3 uses the formula \(\frac{1}{2}\theta\) for the area of a sector, but this formula is based on the formula \(\pi r^2\) for the area of a circle, a complete proof of which requires integral calculus.
The first inequality yields \(\sin\theta\leq\theta\), and because \(\theta > 0\), we obtain \[\frac{\sin\theta}{\theta}\leq 1 \tag{4}\]
Next, multiply the second inequality in (3) by \(\frac{2\cos\theta}{\theta}\) to obtain\[\cos\theta\leq\frac{\sin\theta}{\theta}\tag{5}\]
The combination of (4) and (5) gives us (1) when \(0 < \theta < \frac{\pi}{2}\). However, the functions in (1) do not change when \(\theta\) is replaced by \(-\theta\) because both \(\cos\theta\) and \(\frac{\sin\theta}{\theta}\) are even functions. Indeed, \(\cos(-\theta) = -\cos\theta\) and\[\frac{\sin(-\theta)}{-\theta} = \frac{-\sin\theta}{-\theta} = \frac{\sin\theta}{\theta}\]
Therefore, (1) holds for \(-\frac{\pi}{2} < \theta < 0\) as well. This completes the proof of Theorem 3.
Proof of Theorem 2
According to Theorem 3,\[\cos\theta\leq\frac{\sin\theta}{\theta}\leq 1\]
Since \(\lim\limits_{\theta\rightarrow 0}\cos\theta = \cos 0 = 1\) and \(\lim\limits_{\theta\rightarrow 0}1 = 1\), the Squeeze Theorem yields \(\lim\limits_{\theta\rightarrow 0}\frac{\sin\theta}{\theta} = 1\), as required. For a proof that \(\lim\limits_{\theta\rightarrow 0}\frac{1- \cos\theta}{\theta} = 0\), see Exercises 51 and 58.
98
In the next example, we evaluate another trigonometric limit. The key idea is to rewrite the function of \(h\) in terms of the new variable \(h=4\theta\).
Example 2 Evaluating a Limit by Changing Variables
Investigate \(\lim\limits_{h\rightarrow 0} \frac{\sin 4h}{h}\) numerically and then evaluate it exactly.
| \(h\) | \(\frac{\sin 4h}{h}\) |
| ±1.0 | −0.75680 |
| ±0.5 | 1.81859 |
| ±0.2 | 3.58678 |
| ±0.1 | 3.89 418 |
| ±0.05 | 3.97 339 |
| ±0.01 | 3.99 893 |
| ±0.005 | 3.999 73 |
Solution The table of values at the left suggests that the limit is equal to 4. To evaluate the limit exactly, we rewrite it in terms of the limit of \(\frac{\sin\theta}{\theta}\) so that Theorem 2 can be applied. Thus, we set \(\theta=4h\) and write\[\frac{\sin 4h}{h} = 4\left(\frac{\sin 4h}{4h}\right) = 4\frac{\sin\theta}{\theta}\]
The new variable \(\theta\) tends to zero as \(h\rightarrow 0\) because \(\theta\) is a multiple of \(h\). Therefore, we may change the limit as \(h\rightarrow 0\) into a limit as \(\theta\rightarrow 0\) to obtain\[\lim\limits_{h\rightarrow 0}\frac{\sin 4h}{h} = \lim\limits_{\theta\rightarrow 0}4\frac{\sin\theta}{\theta} = 4\left(\lim\limits_{\theta\rightarrow 0}\frac{\sin\theta}{\theta}\right) = 4(1) = 4\tag{6}\]
Trigonometric Limits Progress Check
Question 2.19 Trigonometric Limits Progress Check
| Find \(\lim\limits_{\theta\rightarrow0}\dfrac{\sin(3\theta)}{\theta}\) | |
|---|---|
| Find \(\lim\limits_{x\rightarrow0}\dfrac{x}{\sin(4x)}\) | |
| Find \(\lim\limits_{t\rightarrow0} \dfrac{\sin(3t)}{\sin(4t)}\) |
2.6.2 Section 2.6 Summary
- We say that \(f(x)\) is squeezed at \(x=c\) if there exist functions \(l(x)\) and \(u(x)\) such that \(l(x)\leq f(x)\leq u(x)\) for all \(x\neq c\) in an open interval \(I\) containing \(c\), and\[\lim\limits_{x\rightarrow c} l(x) = \lim\limits_{x\rightarrow c} u(x) =L\]The Squeeze Theorem states that in this case, \(\lim\limits_{x\rightarrow c} f(x) = L\).
- Two important trigonometric limits:\[\lim\limits_{\theta\rightarrow 0}\frac{\sin\theta}{\theta} = 1, \qquad\lim\limits_{\theta\rightarrow 0}\frac{1 - \cos\theta}{\theta} = 0\]