3.10 Implicit Differentiation

We have developed the basic techniques for calculating a derivative \(\frac{dy}{dx}\) when \(y\) is given in terms of \(x\) by a formula—such as \(y = x^{3} + 1\). But suppose that \(y\) is determined instead by an equation such as

\[y^4 + xy = x^3 - x +2\tag{1}\]

189

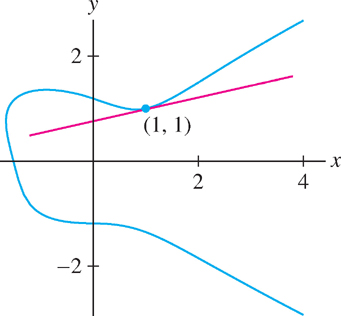
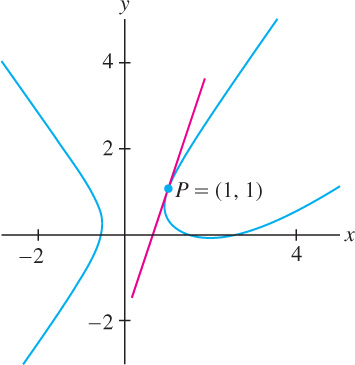
In this case, we say that \(y\) is defined implicitly as a function of \(x\), as opposed to explicitly as \(y=f(x)\). How can we find the slope of the tangent line at a point on the graph (Figure 3.59)? Although it may be difficult or even impossible to solve for \(y\) explicitly as a function of \(x\), we can find \(\frac{dy}{dx}\) using the method of implicit differentiation.

Figure 3.59: Plot of \(y^{4} + xy = x^{3} - x + 2\)

To illustrate, consider the equation of the unit circle (Figure 3.60):

\[x^{2} + y^{2} = 1\]

Figure 3.60: The tangent line to the unit circle \(x^2+y^2=1\) at \(P(\frac{3}{5},\frac{4}{5})\) has slope \(-\frac{3}{4}\).

Compute \(\frac{dy}{dx}\) by taking the derivative of both sides of the equation:

\begin{align*} \frac{d}{dx}(x^2+y^2)&=\frac{d}{dx}(1)\\ \frac{d}{dx}(x^2) + \frac{d}{dx}(y^2)&=0\\ 2x + \frac{d}{dx}(y^2)&=0 \tag{2} \end{align*}

How do we handle the term \(\frac{d}{dx}(y^2)\)? We use the Chain Rule. Think of \(y\) as a function \(y = f(x)\). Then \(y^{2} = f(x)^{2}\) and by the Chain Rule,

\[ \frac{d}{dx}y^2 = \frac{d}{dx}f(x)^2 = 2f(x)\frac{df}{dx} = 2y\frac{dy}{dx} \]

or, in Leibniz notation,

\[ \frac{d}{dx}y^2 = \frac{d}{dy}y^2\frac{dy}{x} = 2y\frac{dy}{dx} \]

Equation (2) becomes \(\displaystyle 2x+2y\frac{dy}{dx} = 0\), and we can solve for \(\displaystyle \frac{dy}{dx}\) if \(y \neq 0\):

\[ \boxed{\dfrac{dy}{dx} = -\dfrac{x}{y}}\tag{3} \]

EXAMPLE 1

Use Eq. (3) to find the slope of the tangent line at the point \(P (\frac{3}{5},\frac{4}{5})\) on the unit circle.

Solution Set \(\displaystyle x= \frac{3}{5}\) and \(\displaystyle y=\frac{4}{5}\) in Eq. (3):

\[ \left.\frac{dy}{dx}\right|_P = -\dfrac{x}{y} = -\dfrac{\frac{3}{5}}{\frac{4}{5}} = -\frac{3}{4} \]

In this particular example, we could have computed dy/dx directly, without implicit differentiation. The upper semicircle is the graph of 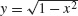and

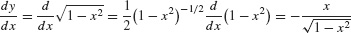
This formula expresses \(\frac{dy}{dx}\) in terms of \(x\) alone, whereas Eq. (3) expresses \(\frac{dy}{dx}\) in terms of both \(x\) and \(y\), as is typical when we use implicit differentiation. The two formulas agree because \(y=\sqrt{1-x^2}\).

Notice what happens if we insist on applying the Chain Rule to \(\frac{d}{dy}\sin y\). The extra factor appears, but it is equal to \(1\):

\[ \frac{d}{dy}\sin y = (\cos y)\frac{dy}{dy} = \cos y \]

Before presenting additional examples, let’s examine again how the factor \(\frac{dy}{dx}\) arises when we differentiate an expression involving \(y\) with respect to \(x\). It would not appear if we were differentiating with respect to \(y\). Thus,

\begin{align*} \frac{d}{dy}\sin y &=\cos y &\text{but}& &\frac{d}{dx}\sin y &= (\cos y)\frac{dy}{dx}\\ \frac{d}{dy}y^4 &= 4y^3 &\text{but} && \frac{d}{dx}y^4 &= 4y^3\frac{dy}{dx} \end{align*}

190

Similarly, the Product Rule applied to \(xy\) yields

\[ \frac{d}{dx}(xy) = x\frac{dy}{dx} + y\frac{dx}{dx} = x \frac{dy}{dx}+y \]

The Quotient Rule applied to \(\displaystyle \frac{t^{2}}{y}\) yields

\[ \frac{d}{dt}\left(\frac{y\frac{d}{dt}t^2 - t^2 \frac{dy}{dt}}{y^2}\right) = \frac{2ty - t^2\frac{dy}{dt}}{y^2} \]

EXAMPLE 2

Find an equation of the tangent line at the point \(P = (1, 1)\) on the curve (Figure 3.59)

\[ y^{4} + xy = x^{3} - x + 2 \]

Solution We break up the calculation into two steps.

Step 1. Differentiate both sides of the equation with respect to x.

\begin{align*} \frac{d}{dx}y^{4} + \frac{d}{dx}(xy) &= \frac{d}{dx}(x^{3} - x + 2)\\[5pt] 4y^3\frac{dy}{dx} + \left(x\frac{dy}{dx} + y\right)&=3x^2 -1\tag{4} \end{align*}

Step 2. Solve for \(\frac{dy}{dx}\).

Move the terms involving \(\frac{dy}{dx}\) in Eq. (4) to the left and place the remaining terms on the right:

\[ 4y^3 \frac{dy}{dx} + x\frac{dy}{dx} = 3x^2-1 - y \]

Then factor out \(\frac{dy}{dx}\) and divide:

\begin{align*} \left(4y^3 + x\right)\frac{dy}{dx}&=3x^2-1 - y\\ \frac{dy}{dx}&= \frac{3x^2-1 - y}{4y^3 + x} \end{align*}

To find the derivative at \(P = (1, 1)\), apply Eq. (5) with \(x = 1\) and \(y = 1\):

\[ \left.\frac{dy}{dx}\right|_{(1,1)} = \frac{3\cdot1^2-1 - 1}{4\cdot1^3 + 1}=\frac{1}{5} \]

An equation of the tangent line is \(y-1 = \frac{1}{5}(x-1)\) or \(y =\frac{1}{5}x + \frac{4}{5}\).

CONCEPTUAL INSIGHT

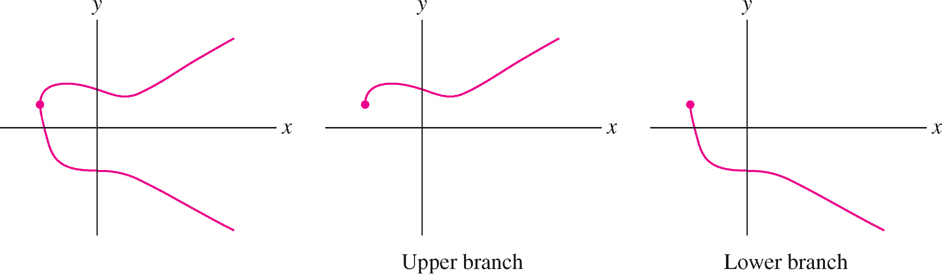
The graph of an equation does not always define a function because there may be more than one \(y\)-value for a given value of \(x\). Implicit differentiation works because the graph is generally made up of several pieces called branches, each of which does define a function (a proof of this fact relies on the Implicit Function Theorem from advanced calculus). For example, the branches of the unit circle \(x^{2} + y^{2} = 1\) are the graphs of the functions \(y=-\sqrt{1-x^2}\) and \(y=\sqrt{1-x^2}\). Similarly, the graph in Figure 3.61 has an upper and a lower branch. In most examples, the branches are differentiable except at certain exceptional points where the tangent line may be vertical.

Figure 3.61: Each branch of the plot of \(y^{4} + xy = x^{3} - x + 2\) defines a function of \(x\).

191

EXAMPLE 3

Find the slope of the tangent line at the point \(P = (1, 1)\) on the graph of \(e^{x - y} = 2x^{2} - y^{2}\).

Solution We follow the steps of the previous example, this time writing \(y'\) for \(\frac{dy}{dx}\):

\begin{align*} \frac{d}{dx}e^{x - y} &= \frac{d}{dx}(2x^{2} - y^{2})\\[5pt] e^{x-y}(1-y')& = 4x - 2yy'&&(\text{Chain Rule applied to }e^{x-y})\\[5pt] e^{x-y} - e^{x-y}y' &= 4x - 2yy'\\[5pt] (2y - e^{x-y})y'&= 4x - e^{x-y} &&(\text{Place all }y'\text{-terms on left})\\[5pt] y' &= \frac{4x - e^{x-y}}{2y - e^{x-y}} \end{align*}

The slope of the tangent line at \(P = (1, 1)\) is (Figure 3.62)

\[ \left.\frac{dy}{dx}\right|_(1,1) = \frac{4(1) - e^{1-1}}{2(1) - e^{1-1}}=\frac{4-1}{2-1} = 3 \]

Figure 3.62: Plot of \(e^{x-y} = 2x^{2} - y^{2}\).

Question 3.25 Implicit Differentiation Progress Check 1

f23KIjn9Gc9DnEdgWdFsZPGQKaDBa6VaLKaE5lRbxpUZTTcDWDO6n/MGVFDFncqMo/J1u6PzD543T67om++Jsc1q9EYQHlTX9fnaZe2J9/Yc0XkyxKi6SBowRvyj6Lf/gU6WT+mrZhU4xurHPY2sQ07kReU=
3
Correct.
Try again. Differentiate implicitly, assuming \(y\) is a function of \(x\). Thus don't forget to use the chain rule when differentiating \(y^3\).
Incorrect.

EXAMPLE 4 Shortcut to Derivative at a Specific Point

Calculate \(\left.\frac{dy}{dt}\right|_P\) at the point \(P=(0,\frac{5\pi}{2})\) on the curve (Figure 3.63):

\[ y \ cos(y + t + t^{2}) = t^{3} \]

Solution As before, differentiate both sides of the equation (we write \(y'\) for \(\frac{dy}{dx}\)):

\begin{align*} \frac{d}{dt}y\cos(y + t + t^{2})&= \frac{d}{dt}t^{3}\\[5pt] y'\cos(y + t + t^{2}) - y\sin(y + t + t^{2})(y'+1+2t) &=3t^2\tag{6} \end{align*}

We could continue to solve for \(y'\), but that is not necessary. Instead, we can substitute \(t = 0\), \(y=\frac{5\pi}{2}\) directly in Eq. (6) to obtain

\begin{align*} y'\cos\left(\frac{5\pi}{2} + 0 + 0^{2}\right) - \frac{5\pi}{2}\sin\left(\frac{5\pi}{2} + 0 + 0^{2}\right)(y'+1+0) &=0\\[5pt] 0 - \left(\frac{5\pi}{2}\right)(1)(y' + 1) = 0 \end{align*}

This gives us \(y' + 1 = 0\) or \(y' = -1\).

Figure 3.63: Plot of \( y \cos(y + t + t^{2}) = t^{3} \). The tangent line at \( P(0,\frac{5\pi}{2})\) has slope -1. move the slider to see the tangent lines to the curve at other points.

192

3.10.1 Section 3.10 Summary

Step 1. Take the derivative of both sides of the equation with respect to \(x\).

Step 2. Solve for \(\frac{dy}{dx}\) by collecting the terms involving \(\frac{dy}{dx}\) on one side and the remaining terms on the other side of the equation.

\[ \frac{d}{dx}\sin y = (\cos y)\frac{dy}{dx} \]