3.3 Product and Quotient Rules
 REMINDER The product function \(fg\) is defined by \( (fg)(x) = f(x) g(x)\).
REMINDER The product function \(fg\) is defined by \( (fg)(x) = f(x) g(x)\).
This section covers the Product Rule and Quotient Rule for computing derivatives. These two rules, together with the Chain Rule and implicit differentiation (covered in later sections), make up an extremely effective “differentiation toolkit.”
THEOREM 1 Product Rule
If \(f\) and \(g\) are differentiable functions, then \(fg\) is differentiable and
\[(fg)'(x) = f(x)g'(x) + g(x)f'(x)\]
In Leibniz notation, the product rule can be written as
\[\frac{d}{dx}\left(fg(x)\right) = f(x)\frac{dg(x)}{dx}+g(x)\frac{df(x)}{dx}\]
It may be helpful to remember the Product Rule in words: The derivative of a product is equal to the first function times the derivative of the second function plus the second function times the derivative of the first function:
\[\text{First}\cdot(\text{Second})' + \text{Second}\cdot(\text{First})'\]
We prove the Product Rule after presenting three examples.
EXAMPLE 1
Find the derivative of \(h(x) = x^{2}(9x + 2)\).
Solution This function is a product:
\[h(x) = \overbrace{x^{2}}^{\text{First}}\;\overbrace{(9x + 2)}^{\text{Second}}\]
By the Product Rule (in Leibniz notation),
\begin{align*}h'(x)&= \overbrace{x^2}^{\text{First}}\;\overbrace{\frac{d}{dx}(9x+2)}^{\text{Second}'} + \overbrace{(9x+2)}^{\text{Second}}\;\overbrace{\frac{d}{dx}(x^2)}^{\text{First}'}\\ &=(x^2)(9) + (9x+2)(2x) = 27x^2 + 4x\end{align*}
EXAMPLE 2
Find the derivative of \(y = (2 + x^{-1})(x^{3/2} + 1)\).
Note how the prime notation is used in the solution to Example 2. We write \( (x^{3/2} + 1)' \) to denote the derivative of \(x^{3/2} + 1\), etc.
Solution Use the Product Rule:
\begin{align*} y'&=\overbrace{(2+x^{-1})(x^{3/2}+1)'+(x^{3/2}+1)(2+x^{-1})'}^{\text{First}\cdot(\text{Second})'\;+\;\text{Second}\cdot(\text{First})'}\\ &=(2+x^{-1})(\tfrac{3}{2}x^{1/2})+(x^{3/2}+1)(-x^{-2})\quad\text{(compute the derivatives)}\\ &=3x^{1/2} + \tfrac{3}{2}x^{-1/2} - x^{-1/2} - x^{-2} = 3x^{1/2} + \tfrac{1}{2}x^{-1/2} - x^{-2}\quad\text{(simplify)} \end{align*}
144
In the previous two examples, we could have avoided the Product Rule by expanding the function. Thus, the result of Example 2 can be obtained as follows:
\begin{align*} y&=(2+x^{-1})(x^{3/2}+1) = 2x^{3/2}+2+x^{1/2}+x^{-1}\\ y'&=\frac{d}{dx}(2x^{3/2}+2+x^{1/2}+x^{-1}) = 3x^{1/2} + \tfrac{1}{2}x^{-1/2} - x^{-2} \end{align*}
Question 3.7 Product and Quotient Rule Progress Check 1
Let \( \displaystyle f(x)=(x^3-2x+17x^{\frac{5}{3}})\) and \( \displaystyle g(x)=x+ \frac{1}{x}\). Use the product rule to find \( \displaystyle \frac{d}{dx} f(x) g(x)\)
| A. |
| B. |
| C. |
| D. |
In the next example, the function cannot be expanded, so we must use the Product Rule (or go back to the limit definition of the derivative).
EXAMPLE 3
Calculate \(\frac{d}{dt}(t^2e^t)\).
Solution Use the Product Rule and the formula \(\frac{d}{dt}e^t=e^t\):
\[\frac{d}{dt}(t^2e^t) = \overbrace{t^2\frac{d}{dt}e^t + e^t\frac{d}{dt}t^2}^{\text{First}\cdot(\text{Second})'\;+\;\text{Second}\cdot(\text{First})'} = t^2e^t+e^t(2t) = (t^2+2t)e^t\]
Question 3.8 Product and Quotient Rule Progress Check 2
Find \(\displaystyle \frac{d}{dt} e^t (t^2+5)\) at \(t=0\).
Proof of the Product Rule
According to the limit definition of the derivative,
\[(fg)'(x) = \lim\limits_{h\rightarrow 0}\frac{f(x+h)g(x+h) - f(x)g(x)}{h}\]
We first rewrite the numerator by subtracting and adding the quantity \(f(x+h)g(x)\), which does not change the value of the expression. Then we factor to obtain
\[f(x + h)g(x + h) - f(x)g(x) = f(x + h) (g(x + h) - g(x)) + g(x) (f(x + h) - f(x))\]
Now use this identity to write \((fg)'(x)\) as a sum of two limits:
\[(fg)'(x) = \underbrace{\lim\limits_{h\rightarrow 0}f(x+h)\frac{g(x+h)-g(x)}{h}}_{\text{Show that this equals }f(x)g'(x)} + \underbrace{\lim\limits_{h\rightarrow 0}g(x)\frac{f(x+h)-f(x)}{h}}_{\text{Show that this equals }g(x)f'(x)}\tag{1}\]
The use of the Sum Law is valid, provided that each limit on the right exists. To check that the first limit exists and to evaluate it, we note that \(f(x)\) is continuous (because it is differentiable) and that \(g(x)\) is differentiable. Thus
\begin{align*}\lim\limits_{h\rightarrow 0}f(x+h)\frac{g(x+h)-g(x)}{h}&=\lim\limits_{h\rightarrow 0}f(x+h)\lim\limits_{h\rightarrow 0}\frac{g(x+h)-g(x)}{h}\\[5pt] &=f(x)g'(x)\tag{2}\end{align*}
The second limit is similar:
\[\lim\limits_{h\rightarrow 0}g(x)\frac{f(x+h)-f(x)}{h} = g(x)\lim\limits_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} = g(x)f'(x)\tag{3}\]
Using Eq. (2) and Eq. (3) in Eq. (1), we conclude that \(fg\) is differentiable and that \((fg)'(x) = f(x)g'(x) + g(x)f '(x)\) as claimed.
145
CONCEPTUAL INSIGHT
The Product Rule was first stated by the 29-year-old Leibniz in 1675, the year he developed some of his major ideas on calculus. To document his process of discovery for posterity, he recorded his thoughts and struggles, the moments of inspiration as well as the mistakes. In a manuscript dated November 11, 1675, Leibniz suggests incorrectly that \((fg)'\) equals \(f'g'\). He then catches his error by taking \(f(x) = g(x) = x\) and noticing that
\[(fg)'(x) = (x^2)' = 2x \text{ is }{not}\text{ equal to }f'(x)g'(x) = 1\cdot1=1\]
Ten days later, on November 21, Leibniz writes down the correct Product Rule and comments “Now this is a really noteworthy theorem.”
With the benefit of hindsight, we can point out that Leibniz might have avoided his error if he had paid attention to units. Suppose \(f(t)\) and \(g(t)\) represent distances in meters, where \(t\) is time in seconds. Then \((fg)'\) has units of \(m^{2}/s\). This cannot equal \(f'g'\), which has units of \((m/s)(m/s) = m^{2}/s^{2}\).
The next theorem states the rule for differentiating quotients. Note, in particular, that \(\left(\frac{f}{g}\right)'\) is not equal to the quotient \(\frac{f'}{g'}\).
THEOREM 2 Quotient Rule
 REMINDER The quotient function \(\frac{f}{g}\) is defined by
REMINDER The quotient function \(\frac{f}{g}\) is defined by
\[\left(\frac{f}{g}\right)(x) = \frac{f(x)}{g(x)}\]
If \(f\) and \(g\) are differentiable functions, then \(\frac{f}{g}\) is differentiable for all \(x\) such that \(g(x) \neq 0\), and
\[\left(\frac{f}{g}\right)'(x)=\frac{g(x)f'(x) - f(x)g'(x)}{g(x)^2}\]
In Leibniz notation, the quotient rule can be written as
\[\frac{d}{dx}\left(\frac{f}{g}(x) \right) = \frac{g(x)\frac{df(x)}{dx}-f(x)\frac{dg(x)}{dx}}{g^2(x)}\]
The numerator in the Quotient Rule is equal to the bottom times the derivative of the top minus the top times the derivative of the bottom:
\[\frac{\text{Bottom}\cdot(\text{Top})' - \text{Top}\cdot(\text{Bottom})'}{\text{Bottom}^2}\]
The proof is similar to that of the Product Rule (see Exercises 58–60).
EXAMPLE 4
Compute the derivative of \(f(x) = \dfrac{x}{1+x^2}\).
Solution Apply the Quotient Rule:
\begin{align*}f'(x) &= \frac{\overbrace{(1+x^2)}^{\text{Bottom}}\;\overbrace{(x)'}^{\text{Top}'}-\overbrace{(x)}^{\text{Top}}\;\overbrace{(1+x^2)'}^{\text{Bottom}'}}{(1+x^2)^2} = \frac{(1+x^2)(1)-(x)(2x)}{(1+x^2)^2}\\ &=\frac{1+x^2-2x^2}{(1+x^2)^2} = \frac{1-x^2}{(1+x^2)^2}\end{align*}
Question 3.9 Product and Quotient Rule Progress Check 3
Use the quotient rule to find the derivative \(\displaystyle \frac{dy}{dx}\) of the function \(y=\frac{x^2+1}{x+\sqrt{x}}\)
| A. |
| B. |
| C. |
| D. |
EXAMPLE 5
Calculate \(\dfrac{d}{dt}\dfrac{e^t}{e^t+t}\).
Solution Use the Quotient Rule and the formula \((e^{t})' = e^{t}\):
\[\frac{d}{dt}\frac{e^t}{e^t+t} = \frac{(e^t+t)(e^t)' - e^t(e^t+t)'}{(e^t+t)^2} = \frac{(e^t+t)e^t - e^t(e^t+1)}{(e^t+t)^2}= \frac{(t-1)e^t}{(e^t+t)^2}\]
146
EXAMPLE 6
Find the tangent line to the graph of \(f(x)=\dfrac{3x^2+x-2}{4x^3+1}\) at \(x = 1\).
Solution
\begin{align*} f'(x)=\frac{d}{dx}\left(\dfrac{3x^2+x-2}{4x^3+1}\right)&= \frac{\overbrace{(4x^3+1)}^{\text{Bottom}}\;\overbrace{(3x^2+x-2)'}^{\text{Top}'}-\overbrace{(3x^2+x-2)}^{\text{Top}}\;\overbrace{(4x^3+1)'}^{\text{Bottom}'}}{(4x^3+1)^2}\\ &=\frac{(4x^3+1)(6x+1) - (3x^2+x-2)(12x^2)}{(4x^3+1)^2}\\ &=\frac{(24x^4+4x^3+6x+1) - (36x^4+12x^3-24x^2)}{(4x^3+1)^2}\\ &=\frac{-12x^4 - 8x^3 + 24x^2 + 6x}{(4x^3+1)^2} \end{align*}
At \(x = 1\),
\begin{align*} f(1)&=\frac{3+1-2}{4+1}=\frac{2}{5}\\ f'(1)&=\frac{-12-8+24+6+1}{5^2} = \frac{11}{25} \end{align*}
An equation of the tangent line at \((1,\tfrac{2}{5})\) is
\[y-\frac{2}{5} = \frac{11}{25}(x-1)\text{ or } y=\frac{11}{25}x - \frac{1}{25}\]
Question 3.10 Product and Quotient Rule Progress Check 4
Find the equation of the tangent line to the curve \( \displaystyle y=\frac{e^x}{x^2+1}\) at the point \( (0,1)\). Give your answer in the form \( y=mx+b\), no spaces.
EXAMPLE 7 Power Delivered by a Battery
The power that a battery supplies to an apparatus such as a laptop depends on the internal resistance of the battery. For a battery of voltage \(V\) and internal resistance \(r\), the total power delivered to an apparatus of resistance \(R\) (Figure 3.26) is
\[P=\frac{V^2R}{(R+r)^2}\]
(a) Calculate \(\dfrac{dP}{dR}\), assuming that \(V\) and \(r\) are constants.
(b) Where, in the graph of \(P\) versus \(R\), is the tangent line horizontal?
Solution
(a) Because \(V\) is a constant, we obtain (using the Quotient Rule)
\[\dfrac{dP}{dR}=V^2\dfrac{d}{dR}\left(\frac{R}{(R+r)^2}\right)=V^2\frac{(R+r)^2\tfrac{d}{dR}R-R\dfrac{d}{dR}(R+r)^2}{(R+r)^4}\tag{4}\]
We have \(\tfrac{d}{dR}R = 1\), and \(\tfrac{d}{dR}r = 0\) because \(r\) is a constant. Thus,
\begin{align*} \frac{d}{dR}(R+r)^2 &=\frac{d}{dR}(R^2+2rR+r^2)\\[5pt] &=\frac{d}{dR}R^2+2r\frac{d}{dR}R+\frac{d}{dR}r^2\\[5pt] &=2R+2r+0 = 2(R+r)\tag{5} \end{align*}
Using Eq. (5) in Eq. (4), we obtain
\[\frac{dP}{dR}=V^2\frac{(R+r)^2 - 2R(R+r)}{(R+r)^4} = V^2\frac{(R+r)-2R}{(R+r)^3} = V^2\frac{r-R}{(R+r)^3}\tag{6}\]
(b) The tangent line is horizontal when the derivative is zero. We see from Eq. (6) that the derivative is zero when \(r - R = 0\) —that is, when \(R = r\).
147
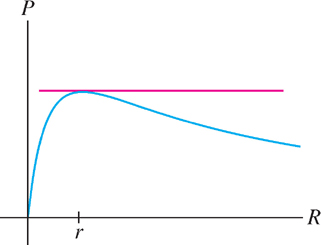
GRAPHICAL INSIGHT
Figure 3.27 shows that the point where the tangent line is horizontal is the maximum point on the graph. This proves an important result in circuit design: Maximum power is delivered when the resistance of the load (apparatus) is equal to the internal resistance of the battery.
3.3.1 Section 3.3 Summary
- Two basic rules of differentiation:
\begin{align*} &\text{Product Rule:}&(fg)'&=fg'+gf'\\ &\text{Quotient Rule:}&\left(\frac{f}{g}\right)' &= \frac{gf' - fg'}{g^2} \end{align*}
- Remember: The derivative of \(fg\) is not equal to \(f'g'\). Similarly, the derivative of \(\frac{f}{g}\) is not equal to \(\frac{f'}{g'}\).