Differentiation

3.5 Higher Derivatives

Higher derivatives are obtained by repeatedly differentiating a function \(y = f(x)\). If \(f'\) is differentiable, then the second derivative, denoted \(f''\) or \(y''\), is the derivative

\[f''(x) = \frac{d}{dx}(f'(x))=\frac{d}{dx} \frac{d}{dx} f(x) = \frac{d}{dx} \frac{d}{dx} y\]

Now, as Leibniz did, multiply the \(d\)'s in the numerator to obtain \(d^2\) and create a shorthand for the \(dx \cdot dx\) in the denominator to write it as \(dx^2\). This then gives us Leibniz's notation for the second derivative of \(y\) with respect to \(x\) as \(\frac{d^2y}{dx^2}\).

The second derivative is the rate of change of \(f'(x)\). The next example highlights the difference between the first and second derivatives.

160

EXAMPLE 1

Calculate \(\frac{dy}{dx}=f'(x)\) and \(\frac{d^2y}{dx^2}=f''(x)\) for \(y= f(x) = \frac{x}{e^x}\).

Solution We must calculate the first and second derivatives:

\(\displaystyle \frac{d}{dx} \frac{x}{e^x}= \frac{e^x-xe^x}{(e^x)^2}= \frac{1-x}{e^x}\)

\(\displaystyle \frac{d^2}{dx^2} \frac{x}{e^x}= \frac{d}{dx} \frac{1-x}{e^x} =\frac{-e^x-(1-x)e^x}{(e^x)^2} = \frac{x-2}{e^x} \)

\(\frac{dy}{dx}\) has units of y per unit of \(x\).
\(\frac{d^{2}y}{dx^{2}}\) has units of \(\frac{dy}{dx}\) per unit of \(x\) or units of \(y\) per unit of \(x^2\).

The process of differentiation can be continued, provided that the derivatives exist. The third derivative, denoted \(f'''(x)\) or \(f^{(3)}(x)\), is the derivative of \(f''(x)\). More generally, the \(n^{\text{th}}\) derivative \(f^{(n)}(x)\) is the derivative of the \((n - 1)^{\text{st}}\) derivative. We call \(f(x)\) the zeroeth derivative and \(f'(x)\) the first derivative. In Leibniz notation, we write

\[\frac{df}{dx},\frac{d^2f}{dx^2},\frac{d^3f}{dx^3},\frac{d^4f}{dx^4},\ldots\]

EXAMPLE 2

Calculate \(f'''(-1)\) for \(f(x) = 3x^{5}- 2x^{2} + 7x^{-2}\).

Solution We must calculate the first three derivatives:

\begin{align*}f'(x) &= \frac{d}{dx}(3x^{5}- 2x^{2} + 7x^{-2})=15x^{4}- 4x -14x^{-3}\\[5pt] f''(x)&= \frac{d}{dx}(15x^{4}- 4x -14x^{-3})= 60x^3-4+42x^{-4}\\[5pt] f''(x)&= \frac{d}{dx}(60x^3-4+42x^{-4}) = 180x^2 - 168x^{-5}\end{align*}

At \(x = -1\), \(f'''(-1) = 180 + 168 = 348\).

Question 3.11 Higher Derivatives Progress Check 1

pxBGKg16ubCrrOEKfj+OJPunje9Cm+GkJ3Qewo7J9rLGvvWKuNruAAdRUejXNC3rcRh8iOvDakS1ULI8

Correct.

Try again. First find \(f'(x)\). Then differentiate again to find \(f''(x)\), and finally plug in \(x=0\) to find \(f''(0)\).

Incorrect.

Polynomials have a special property: Their higher derivatives are eventually the zero function. More precisely, if \(f(x)\) is a polynomial of degree \(k\), then \(f^{(n)}(x)\) is zero for \(n > k\). Table 2 illustrates this property for \(f(x) = x^{5}\). By contrast, the higher derivatives of a nonpolynomial function are never the zero function (see Exercise 85, Section 4.9).

\(f(x)\)	\(f'(x)\)	\(f''(x)\)	\(f'''(x)\)	\(f^{(4)}(x)\)	\(f^{(5)}(x)\)	\(f^{(6)}(x)\)
\(x^5\)	\(5x^{4}\)	\(20x^{3}\)	\(60x^{2}\)	\(120x\)	120	0

Higher Derivatives Progress Check 2

Question 3.12 Higher Derivatives Progress Check 2

\(\displaystyle \frac{dx^4}{dx}\) evaluated at \(x=-1\)	sWNiRN4ZHUU=
\(\displaystyle\frac{d^2x^4}{dx^2}\) evaluated at \(x=-1\)	DDH6Tw1RFEk=
\(\displaystyle\frac{d^3x^4}{dx^3}\) evaluated at \(x=-1\)	YnykAIZUglk=
\(\displaystyle\frac{d^4x^4}{dx^4}\) evaluated at \(x=-1\)	7dfNq0tWt7c=
\(\displaystyle\frac{d^5x^4}{dx^5}\) evaluated at \(x=-1\)	1Wh3cvJ2xF4=

Correct.

Try again.

Incorrect.

161

EXAMPLE 3

Calculate the first four derivatives of \(y = x^{-1}\). Then find the pattern and determine a general formula for \(y^{(n)}\).

Solution By the Power Rule,

\(y'(x) = -x^{-2}\),\(y = 2x^{-3}\),\(y = -2(3)x^{-4}\),\(y^{(4)} = 2(3)(4)x^{-5}\)

REMINDER \(n\)-factorial is the number

\[n!=n(n-1)(n-1)\cdots(2)(1)\]

Thus

\[1!=1,2!=(2)(1)=2,3!=(3)(2)(1)=6\]

By convention, we set \(0! = 1\).

We see that \(y^{(n)}(x)\) is equal to \(\pm n! x^{-n-1}\). Now observe that the sign alternates. Since the odd-order derivatives occur with a minus sign, the sign of \(y^{(n)}(x)\) is \((-1)^{n}\). In general, therefore, \(y^{(n)}(x) = (-1)^{n}n! x^{-n-1}\).

EXAMPLE 4

Calculate the first three derivatives of \(f(x) = xe^{x}\). Then determine a general formula for \(f^{(n)}(x)\).

Solution Use the Product Rule:

It is not always possible to find a simple formula for the higher derivatives of a function. In most cases, they become increasingly complicated.

\begin{align*}f'(x)&=\frac{d}{dx}(xe^x) = xe^x+e^x=(x+1)e^x\\[5pt] f''(x)&=\frac{d}{dx}((x+1)e^x))=(x+1)e^x + e^x = (x+2)e^x\\[5pt] f'''(x)&=\frac{d}{dx}((x+2)e^x)=(x+2)e^x + e^x = (x+3)e^x\end{align*}

We see that \(f^{n}(x) = f^{n-1}(x) + e^{x}\), which leads to the general formula

\[f^{(n)}(x) = (x + n)e^{x}\]

Question 3.13 Higher Derivatives Progress Check 3

P8wDotr7O+a94zaXejbwxp9QlBcELnQh+SUIvodHdtiz6EOWCYF+mO2DkhNALMlTWAgOV2Fp/3k5dm/ZBNccvxKddaw6s+Pd/atZ6+SMJkgs6biL2njHBjxA+szjAKUf9oKicR9NIaoACu3zyxfNJI3bC7UXO7/Qj/riRFXbt21rB1eBHQ6atpAug0OsmLCeGC9TwW98EugiBoedqyIEPg==

Correct.

Try again.

Incorrect.

One familiar second derivative is acceleration. An object in linear motion with position \(s(t)\) at time \(t\) has velocity \(v(t) = s'(t)\) and acceleration \(a(t) = v'(t) = s''(t)\). Thus, acceleration is the rate at which velocity changes and is measured in units of velocity per unit of time or “distance per time squared” such as \(\text{m/s}^{2}\).

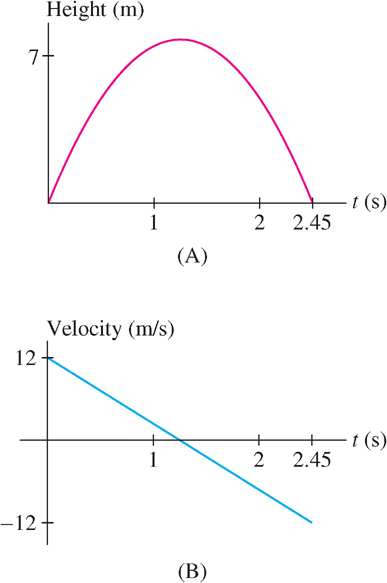
EXAMPLE 5 Acceleration Due to Gravity

Find the acceleration \(a(t)\) of a ball tossed vertically in the air from ground level with an initial velocity of 12 m/s. How does \(a(t)\) describe the change in the ball’s velocity as it rises and falls?

Solution The ball’s height at time \(t\) is \(s(t) = s_{0} + v_{0}t - 4.9t^{2}\text{ m}\) by Galileo’s formula [Figure 3.38(A)]. In our case, \(s_{0} = 0\) and \(v_{0} = 12\), so \(s(t) = 12t - 4.9t^{2}\text{ m}\). Therefore, \(v(t) = s'(t) = 12 - 9.8t\text{ m/s}\) and the ball’s acceleration is

\(a(t)=s''(t) = \frac{d}{dt}(12-9.8t) = -9.8\text{ m/s}^2\)

As expected, the acceleration is constant with value \(-g = -9.8\text{ m/s}^{2}\). As the ball rises and falls, its velocity decreases from 12 to -12 m/s at the constant rate \(-g\) [Figure 3.38(B)].

Figure 3.38: Height and velocity of a ball tossed vertically with initial velocity 12 m/s.

GRAPHICAL INSIGHT

Can we visualize the rate represented by \(f''(x)\)? The second derivative is the rate at which \(f'(x)\) is changing, so \(f''(x)\) is large if the slopes of the tangent lines change rapidly, as in Figure 3.39(A) below. Similarly, \(f''(x)\) is small if the slopes of the tangent lines change slowly—in this case, the curve is relatively flat, as in Figure 3.39(B). If \(f\) is a linear function [Figure 3.39(C)], then the tangent line does not change at all and \(f''(x) = 0\). Thus, \(f''(x)\) measures the “bending” or concavity of the graph.

Figure 3.39: An applet to explore the relationship of the second derivative \(f''(x)\) and the shape of the graph of \(y=f(x)\).

162

EXAMPLE 6

Identify curves I and II in Figure 3.40(B) as the graphs of \(f'(x)\) or \(f''(x)\) for the function \(f(x)\) in Figure 3.40(A).

Solution The slopes of the tangent lines to the graph of \(f(x)\) are increasing on the interval \([a, b]\). Therefore \(f'(x)\) is an increasing function and its graph must be II. Since \(f''(x)\) is the rate of change of \(f'(x)\), \(f''(x)\) is positive and its graph must be I.

Figure 3.40: ---

3.5.1 Section 3.5 Summary

The higher derivatives \(f',f'',f''',\ldots\) are defined by successive differentiation:

\[f''(x) = \frac{d}{dx}f'(x),f'''(x) = \frac{d}{dx}f''(x),\ldots\]

The \(n^{\text{th}}\) derivative is denoted \(f^{(n)}(x)\).

The second derivative plays an important role: It is the rate at which \(f'\) changes. Graphically, \(f''\) measures how fast the tangent lines change direction and thus measures the “bending” of the graph.
If \(s(t)\) is the position of an object at time \(t\), then \(s'(t)\) is velocity and \(s''(t)\) is acceleration.