3.6 Trigonometric Functions
CAUTION In Theorem 1 we are differentiating with respect to \(x\) measured in radians. The derivatives of sine and cosine with respect to degrees involves an extra, unwieldy factor of \(\pi /180\).
We can use the rules developed so far to differentiate functions involving powers of \(x\), but we cannot yet handle the trigonometric functions. What is missing are the formulas for the derivatives of the functions \(\sin x \) and \(\cos x\). Fortunately, their derivatives are simple—each is the derivative of the other up to a sign.
Recall our convention: Angles are measured in radians, unless otherwise specified.
THEOREM 1 Derivative of Sine and Cosine
The functions \(y = \sin x\) and \(y = \cos x\) are differentiable and
\[\boxed{\dfrac{d}{dx}\sin x = \cos x \quad\text{and}\quad \dfrac{d}{dx}\cos x = -\sin x}\]
Proof
We must go back to the definition of the derivative:
\[\frac{d}{dx}\sin x = \lim\limits_{h\rightarrow 0}\frac{\sin(x+h) - \sin x}{h}\tag{1}\]
REMINDER Addition formula for \( \sin x\):
\( \sin(x+h) = \sin x \cos h + \cos x \sin h \)
We cannot cancel the \(h\) by rewriting the difference quotient, but we can use the addition formula (see marginal note) to write the numerator as a sum of two terms:
\begin{align*}\sin(x+h) - \sin x&= \sin x \cos h + \cos x \sin h - \sin x\quad\text{(addition formula)}\\ &=(\sin x\cos h - \sin x) + \cos x \sin h\\ &=\sin x (\cos h - 1) + \cos x \sin h\end{align*}
This gives us
\begin{align*}\frac{\sin(x+h) - \sin x}{h}&=\frac{\sin x (\cos h - 1)}{h} + \frac{\cos x \sin h}{h}\\[10pt] \frac{d\sin x}{dx}=\lim\limits_{h\rightarrow 0}\frac{\sin(x+h) - \sin x}{h}&=\lim\limits_{h\rightarrow 0}\frac{\sin x (\cos h - 1)}{h} + \lim\limits_{h\rightarrow 0}\frac{\cos x \sin h}{h}\\[10pt] &=(\sin x)\lim\limits_{h\rightarrow 0}\frac{\cos h - 1}{h} + (\cos x)\lim\limits_{h\rightarrow 0}\frac{\sin h}{h}\tag{2}\end{align*}
Here, we can take \(\sin x\) and \(\cos x\) outside the limits in Eq. (2) because they do not depend on \(h\). The two limits are given by Theorem 2 in Section 2.6,
\[\lim\limits_{h\rightarrow 0}\frac{\cos h - 1}{h}=0\quad\text{and}\quad\lim\limits_{h\rightarrow 0}\frac{\sin h}{h}= 1\]
Therefore, Eq. (2) reduces to the formula \(\frac{d}{dx}\sin x = \cos x\), as desired. The formula \(\frac{d}{dx}\cos x = -\sin x\) is proved similarly (see Exercise 53).
EXAMPLE 1
Calculate \(f''(x)\), where \(f(x) = x \cos x\).
Solution By the Product Rule,
\begin{align*}f'(x)&=x\frac{d}{dx}\cos x + \cos x\frac{d}{dx}x = x(-\sin x) + \cos x = \cos x - x \sin x\\ f''(x) &= (\cos x - x\sin x)' = -\sin x - (x(\sin x)' + \sin x)=-2\sin x - x\cos x\end{align*}
Question 3.14 Trigonometric Functions Progress Check 1
+iyifxqtJbNAqNsJvFckyKU3MMw0UBgujzuOMEOdgWNNxg8QbvFNIgCSgMr+NXH74nlir5cYPOA8Ijg0UBjXFjavV45KgbXv5/+XuTCT4eiUHUiYYRP8Kz0S1KTekC+BJ9397op98cSlEJDpf99qvbKBE1prhYASiUVerw==166
GRAPHICAL INSIGHT
The formula \((\sin x)' = \cos x\) is made plausible when we compare the graphs in Figure 3.41. The tangent lines to the graph of \(y = \sin x\) have positive slope on the interval \((-\frac{\pi}{2},\frac{\pi}{2})\), and on this interval, the derivative \(y' = \cos x\) is positive. Similarly, the tangent lines have negative slope on the interval \((\frac{\pi}{2},\frac{3\pi}{2})\) where \(y' = \cos x\) is negative. The tangent lines are horizontal at \(x=-\frac{\pi}{2},\frac{\pi}{2},\frac{3\pi}{2}\), where \(\cos x = 0\).
Question 3.15 Trigonometric Functions Progress Check 2
ThWtRysiQQjZveaFuLF2ZPugINEVritoMcuTGc+AUnypymnkA21NSC5aR2iWngz3ZqOeoajU0g3FM3D8R7XHxQ==
REMINDER The standard trigonometric functions are defined in Section 3.9.
The derivatives of the other standard trigonometric functions can be computed using the Quotient Rule. We derive the formula for \((\tan' x)\) in Example 2 and leave the remaining formulas for the exercises (Exercises 35–37).
THEOREM 2 Derivatives of Standard Trigonometric Functions
\begin{align*}\frac{d}{dx}\tan x &= \sec^2x&\frac{d}{dx}\sec x &=\sec x \tan x\\[5pt] \frac{d}{dx}\cot x & = -\csc^2 x &\frac{d}{dx}\csc x &= -\csc x \cot x \end{align*}
EXAMPLE 2
Verify the formula \(\dfrac{d}{dx}\tan x = \sec^2x\) (Figure 3.42).
Solution Use the Quotient Rule and the identity \(\cos^{2}x + \sin^{2}x = 1\):
\begin{align*}\frac{d}{dx}\tan x &= \left(\frac{\sin x}{\cos x}\right)' = \frac{\cos x\cdot(\sin x)' - \sin x\cdot(\cos x)'}{\cos^2x}\\[10pt] &=\frac{\cos x \cos x - \sin x(-\sin x)}{\cos^2x}\\[10pt] &=\frac{\cos^2x+\sin^2x}{\cos^2x}=\frac{1}{\cos^2x}=\sec^2x\end{align*}
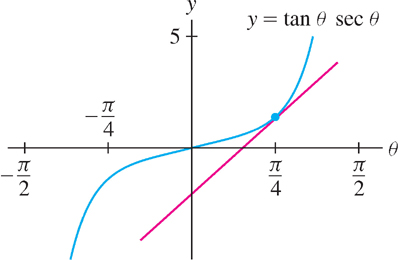
EXAMPLE 3
Find the tangent line to the graph of \(y = \tan\theta\sec\theta \) at \(\theta=\frac{\pi}{4}\)
Solution By the Product Rule,
\begin{align*}y'&=\tan\theta(\sec\theta)' + \sec\theta(\tan\theta)' = \tan\theta(\sec\theta\tan\theta)+\sec\theta\sec^2\theta\\ &=\tan^2\theta\sec\theta + \sec^3\theta\end{align*}
167
Now use the values \(\sec\theta\frac{\pi}{4}=\sqrt{2}\) and \(\tan\theta\frac{\pi}{4}=1\) to compute
\begin{align*}y\left(\frac{\pi}{4}\right)&=\tan\left(\frac{\pi}{4}\right)\sec\left(\frac{\pi}{4}\right) = \sqrt{2}\\[10pt] y'\left(\frac{\pi}{4}\right)&=\tan^2\left(\frac{\pi}{4}\right)\sec\left(\frac{\pi}{4}\right) + \sec^3\left(\frac{\pi}{4}\right) = \sqrt{2} + 2\sqrt{2} = 3\sqrt{2}\end{align*}
An equation of the tangent line (Figure 3.43) is \(y-\sqrt{2} = 3\sqrt{2}(\theta-\frac{\pi}{4})\).
Question 3.16 Trigonometric Functions Progress Check
cpGPjeZoK/v1l7eE7T+F2OmXOxbeAsTeem7BCkYBkZCZF1QkXADrdlGA47oHUp6i9e86yAkDSoVg69cQZf4Lmn4rc7EREzTLX2ZNme89jh5+A2Zc4JQh52XQikXj06aH8UDYBSLdjHFrm5aR5BYhVSCK35SyRJcdzOb3iN8tyrA3v3PB3.6.1 Section 3.6 Summary
- Basic trigonometric derivatives:
\[\frac{d}{dx}\sin x = \cos x\quad\text{and}\quad\frac{d}{dx}\cos x = -\sin x\]
- Additional formulas:
\begin{align*}\frac{d}{dx}\tan x &= \sec^2x&\frac{d}{dx}\sec x &=\sec x \tan x\\[5pt] \frac{d}{dx}\cot x & = -\csc^2 x &\frac{d}{dx}\csc x &= -\csc x \cot x \end{align*}