4.5 L’Hôpital’s Rule
L’Hôpital’s Rule is named for the French mathematician Guillaume François Antoine Marquis de L’Hôpital (1661–1704), who was initially credited as the author of the first textbook on calculus in 1696. The name L’Hôpital is pronounced “Lo-pee-tal.” In fact, the real author was the Swiss mathematician Johann Bernoulli. L'Hôpital merely translated it from German into French.
L’Hôpital’s Rule is a valuable tool for computing certain limits that are otherwise difficult to evaluate, and also for determining “asymptotic behavior” (limits at infinity). We will use it for graph sketching in the next section.
Consider the limit of a quotient
\[ \lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)} \]
Roughly speaking, L’Hôpital’s Rule states that when \(\frac{f(x)}{g(x)}\) has an indeterminate form of type \(\frac{0}{0}\) or \(\frac{\infty}{\infty}\) at \(x = a\), then we can replace \(\frac{f(x)}{g(x)}\) by the quotient of the derivatives \(\frac{f'(x)}{g'(x)}\).
THEOREM 1 L’Hôpital’s Rule
Assume that \(f(x)\) and \(g(x)\) are differentiable on an open interval containing \(a\) and that
\[f(a) = g(a) = 0\]
Also assume that \(g'(x) \neq 0\) (except possibly at \(a\)). Then
\[ \boxed{\lim\limits_{x\rightarrow a}\dfrac{f(x)}{g(x)} = \lim\limits_{x\rightarrow a}\dfrac{f'(x)}{g'(x)}} \]
if the limit on the right exists or is infinite (\(\infty\) or \(-\infty\)). This conclusion also holds if \(f(x)\) and \(g(x)\) are differentiable for \(x\) near (but not equal to) \(a\) and
\[\lim\limits_{x\rightarrow a} f(x) = \pm\infty\quad\text{and}\quad\lim\limits_{x\rightarrow a}g(x)=\pm\infty\]
Furthermore, this rule is valid for one-sided limits.
242
Example 1
Use L’Hôpital’s Rule to evaluate \(\lim\limits_{x\rightarrow 2}\dfrac{x^3-8}{x^4+2x-20}.\)
Solution Let \(f(x) = x^{3} -8\) and \(g(x) = x^{4} + 2x - 20\). Both \(f\) and \(g\) are differentiable and \(\frac{f(x)}{g(x)}\) is indeterminate of type \(\frac{0}{0}\) at \(a = 2\) because \(f(2) = g(2) = 0\):
- Numerator: \(f(2) = 2^{3} - 8 = 0\)
- Denominator: \(g(2) = 2^{4} + 2(2) - 20 = 0\)
Furthermore, \(g'(x) = 4x^{3} + 2\) is nonzero near \(x = 2\), so L’Hôpital’s Rule applies. We may replace the numerator and denominator by their derivatives to obtain
CAUTION When using L’Hópital’s Rule, be sure to take the derivative of the numerator and denominator separately:
\[ \boxed{\lim\limits_{x\rightarrow a}\dfrac{f(x)}{g(x)} = \lim\limits_{x\rightarrow a}\dfrac{f'(x)}{g'(x)}} \]
Do not differentiate the quotient function \(\frac{f(x)}{g(x)}\).
\[ \lim\limits_{x\rightarrow 2}\frac{x^3-8}{x^4+2x-20} = \lim\limits_{x\rightarrow 2}\frac{3x^2}{4x^3+2}=\frac{3(2)^2}{4(2)^3+2} = \frac{6}{17} \]
Example 2
Evaluate \(\lim\limits_{x\rightarrow 2}\dfrac{4-x^2}{\sin\pi x}\).
Solution The quotient is indeterminate of type \(\frac{0}{0}\) at \(x = 2\):
- Numerator: \(4 - x^{2} = 4 - 2^{2} = 0\)
- Denominator: \(\sin \pi x = \sin 2\pi = 0\)
The other hypotheses (that \(f\) and \(g\) are differentiable and \(g'(x) \neq 0\) for \(x\) near \(a = 2\)) are also satisfied, so we may apply L’Hôpital’s Rule:
\[ \lim\limits_{x\rightarrow 2}\frac{4-x^2}{\sin\pi x} = \lim\limits_{x\rightarrow 2}\frac{(4-x^2)'}{(\sin\pi x)'} = \lim\limits_{x\rightarrow 2}\frac{-2x}{\pi\cos \pi x}= \frac{-2(2)}{\pi\cos 2\pi} = \frac{-4}{\pi} \]
Question 4.16 L'Hôpital's Rule Progress Check 1
Calculate \(\displaystyle \lim \limits_{x \longrightarrow 1} \frac{x^{10}-1}{x^2-1}\)
Example 3
Evaluate \(\lim\limits_{x\rightarrow \tfrac{\pi}{2}}\dfrac{\cos^2x}{1-\sin x}\).
Solution Again, the quotient is indeterminate of type \(\frac{0}{0}\) at \(x=\frac{\pi}{2}\):
\[ \cos^2\left(\frac{\pi}{2}\right)=0,\quad 1-\sin\left(\frac{\pi}{2}\right) = 1-1=0 \]
The other hypotheses are satisfied, so we may apply L’Hôpital’s Rule:
\[ \lim\limits_{x\rightarrow \tfrac{\pi}{2}}\dfrac{\cos^2x}{1-\sin x}= \lim\limits_{x\rightarrow \tfrac{\pi}{2}}\dfrac{(\cos^2x)'}{(1-\sin x)'} = \underbrace{ \lim\limits_{x\rightarrow \tfrac{\pi}{2}}\dfrac{-2\cos x\sin x}{-\cos x}}_{\text{L'Hôpital's Rule}}= \underbrace{ \lim\limits_{x\rightarrow \tfrac{\pi}{2}}(2\sin x)}_{\text{Simplify}} =2 \]
Note that the quotient \(\frac{-2\cos x\sin x}{-\cos x}\) is still indeterminate at \(x = \frac{\pi}{2}\). We removed this indeterminacy by cancelling the factor \(-\cos x\).
Question 4.17 L'Hôpital's Rule Progress Check 2
Calculate \(\displaystyle \lim \limits_{x \longrightarrow 0} \frac{\sin (4x)}{x}\)
Example 4 The Form \(0\cdot\infty\)
Evaluate \(\lim\limits_{x\rightarrow 0^+}x\ln x\).
Solution This limit is one-sided because \(f(x) = x \ln x\) is not defined for \(x \leq 0\). Furthermore, as \(x \rightarrow 0+\),
- \(x\) approaches 0,
- \(\ln x\) approaches \(-\infty\).
So \(f(x)\) presents an indeterminate form of type \(0 \cdot \infty\) . To apply L’Hôpital’s Rule we rewrite our function as \(f(x) = \frac{\ln x}{x^{-1}}\) so that \(f(x)\) presents an indeterminate form of type \(-\frac{\infty}{\infty}\). Then L’Hôpital’s Rule applies:
243
\[ \lim\limits_{x\rightarrow 0^+}x\ln x = \lim\limits_{x\rightarrow 0^+}\frac{\ln x}{x^{-1}} = \lim\limits_{x\rightarrow 0^+}\frac{(\ln x)'}{(x^{-1})'} =\underbrace{\lim\limits_{x\rightarrow 0^+}\left(\frac{x^{-1}}{-x^{-2}}\right)}_{\text{L'Hôpital's Rule}}=\underbrace{ \lim\limits_{x\rightarrow 0^+}(-x)}_{\text{Simplify}} = 0 \]
Example 5 Using L’Hôpital’s Rule Twice
Evaluate \(\lim\limits_{x\rightarrow 0}\dfrac{e^x -x -1}{\cos x -1}\).
Solution For \(x = 0\), we have
\[ e^x-x-1 = e^0 - 0 - 1 =0\text{ and }\cos x-1 = \cos0-1=0. \]
A first application of L’Hôpital’s Rule gives
\[ \lim\limits_{x\rightarrow 0}\frac{e^x -x -1}{\cos x -1} = \lim\limits_{x\rightarrow 0}\frac{(e^x -x -1)'}{(\cos x -1)'} = \lim\limits_{x\rightarrow 0}\left(\frac{e^x-1}{-\sin x}\right)= \lim\limits_{x\rightarrow 0}\frac{1-e^x}{\sin x} \]
This limit is again indeterminate of type 0/0, so we apply L’Hôpital’s Rule again:
\[ \lim\limits_{x\rightarrow 0}\frac{1-e^x}{\sin x} = \lim\limits_{x\rightarrow 0}\frac{-e^x}{\cos x} = \frac{-e^0}{\cos0}=-1 \]
Example 6 Assumptions Matter
Can L’Hôpital’s Rule be applied to \(\lim\limits_{x\rightarrow 1}\dfrac{x^2 + 1}{2x+1}\)?
Solution The answer is no. The function does not have an indeterminate form because
\[ \left.\frac{x^2 + 1}{2x+1}\right|_{x=1} = \frac{1^2 + 1}{2\cdot1+1}=\frac{2}{3} \]
However, the limit can be evaluated directly by substitution: \(\lim\limits_{x\rightarrow 1}\frac{x^2 + 1}{2x+1} = \frac{2}{3}\). An incorrect application of L’Hôpital’s Rule gives the wrong answer:
\[ \lim\limits_{x\rightarrow 1}\frac{(x^2 + 1)'}{(2x+1)'} = \lim\limits_{x\rightarrow 1}\frac{2x}{2}=1\quad\text{(not equal to original limit)} \]
Example 7 The Form \(\infty-\infty\)
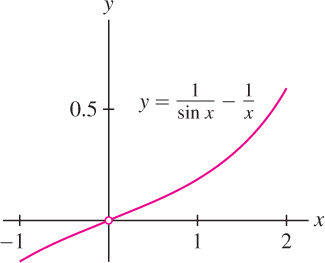
Evaluate \(\lim\limits_{x\rightarrow 0}\left(\dfrac{1}{\sin x} - \dfrac{1}{x}\right)\).
Solution Both \(\frac{1}{\sin x}\) and \(\frac{1}{x}\) become infinite at \(x = 0\), so we have an indeterminate form of type \(\infty - \infty\) . We must rewrite the function as
\[ \dfrac{1}{\sin x} - \dfrac{1}{x} = \frac{x-\sin x}{x\sin x} \]
to obtain an indeterminate form of type \(\frac{0}{0}\). L’Hôpital’s Rule yields (see Figure 4.48):
\begin{align*} \lim\limits_{x\rightarrow 0}\left(\dfrac{1}{\sin x} - \dfrac{1}{x}\right) &= \lim\limits_{x\rightarrow 0}\frac{x-\sin x}{x\sin x} =\underbrace{ \lim\limits_{x\rightarrow 0}\frac{1-\cos x}{x\cos x + \sin x}}_{\text{L'Hôpital's Rule}}\\[5pt] &=\underbrace{\lim\limits_{x\rightarrow 0}\frac{\sin x}{-x\sin x+2\cos x}}_{\text{L'Hôpital's Rule needed again}}=\frac{0}{2} = 0 \end{align*}
Question 4.18 L'Hôpital's Rule Progress Check 3
Calculate \(\displaystyle \lim \limits_{x \longrightarrow 0^+} \Big( \frac{1}{x^2}-\frac{1}{x} \Big) \)
| A. |
| B. |
| C. |
| D. |
Limits of functions of the form \(f(x)^{g(x)}\) can lead to the indeterminate forms \(0^{0}\), \(1^{\infty }\), or \(\infty ^{0}\). In such cases, take the logarithm and then apply L’Hôpital’s Rule.
244
Example 8 The Form \(0^0\)
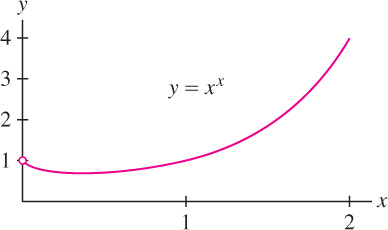
Evaluate \(\lim\limits_{x\rightarrow 0^+}x^x\).
It is a fascinating question: what happens to \(x^x\) as \(x > 0 \) gets closer to 0. It is difficult enough to understand \(x^x\) and \(\lim\limits_{x\rightarrow 0^+}x^x\) is a limit that is hard to guess. However, using algebra and L'Hôpital's rule, we can calculate this limit.
Solution First, compute the limit of the logarithm \(\ln x^{x} = x \ln x\):
\[ \lim\limits_{x\rightarrow 0^+}\ln x^{x} = \lim\limits_{x\rightarrow 0^+}x\ln x = \lim\limits_{x\rightarrow 0^+}\frac{\ln x}{x^{-1}} = 0\quad\text{(by Example 4)} \]
Since \(f(x) = e^{x}\) is continuous, we can exponentiate to obtain the desired limit (see Figure 4.49):
\[ \lim\limits_{x\rightarrow 0^+} x^x = \lim\limits_{x\rightarrow 0^+} e^{\ln x^x}= e^{\big(\lim\limits_{x\rightarrow 0^+} \ln x^x\big)}=e^0=1 \]
4.5.1 Comparing Growth of Functions
Sometimes, we are interested in determining which of two functions, \(f(x)\) and \(g(x)\), grows faster. For example, there are two standard computer algorithms for sorting data (alphabetizing, ordering according to rank, etc.): Quick Sort and Bubble Sort. The average time required to sort a list of size \(n\) has order of magnitude \(n \ln n\) for Quick Sort and \(n^{2}\) for Bubble Sort. Which algorithm is faster when the size \(n\) is large? Although \(n\) is a whole number, this problem amounts to comparing the growth of \(f(x) = x \ln x\) and \(g(x) = x^{2}\) as \(x \rightarrow \infty\).
We say that \(f(x)\) grows faster than \(g(x)\) if
\[ \lim\limits_{x\rightarrow \infty}\frac{f(x)}{g(x)}=\infty \text{ or equivalently }\lim\limits_{x\rightarrow \infty} \frac{g(x)}{f(x)}=0 \]
To indicate that \(f(x)\) grows faster than \(g(x)\), we use the notation \(g(x) \ll f(x)\). For example, \(x \ll x^{2}\) because
\[ \lim\limits_{x\rightarrow \infty} \frac{x^2}{x} = \lim\limits_{x\rightarrow \infty}x = \infty \]
To compare the growth of functions, we need a version of L’Hôpital’s Rule that applies to limits at infinity.
THEOREM 2 L’Hôpital’s Rule for Limits at Infinity
Assume that \(f(x)\) and \(g(x)\) are differentiable in an interval \((b, \infty )\) and that \(g'(x) \neq 0\) for \(x > b\). If \(\lim\limits_{x\rightarrow \infty}f(x)\) and \(\lim\limits_{x\rightarrow \infty}g(x)\) exist and either both are zero or both are infinite, then
\[ \boxed{\lim\limits_{x\rightarrow \infty}\dfrac{f(x)}{g(x)} = \lim\limits_{x\rightarrow \infty}\dfrac{f'(x)}{g'(x)}} \]
provided that the limit on the right exists. A similar result holds for limits as \(x \rightarrow -\infty\) .
Example 9 The Form \(\frac{\infty}{\infty}\)
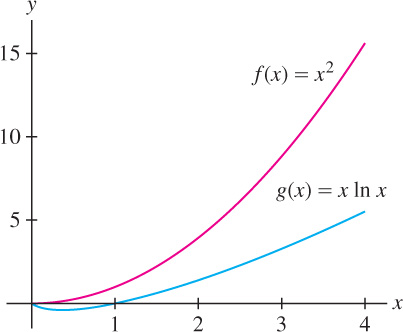
Which of \(f(x) = x^{2}\) and \(g(x) = x \ln x\) grows faster as \(x \rightarrow \infty\) ?
Solution Both\( f(x)\) and \(g(x)\) approach infinity as \(x \rightarrow \infty\) , so L’Hôpital’s Rule applies to the quotient:
\[ \lim\limits_{x\rightarrow \infty}\frac{f(x)}{g(x)}= \lim\limits_{x\rightarrow \infty}\frac{x^2}{x\ln x}= \lim\limits_{x\rightarrow \infty}\frac{x}{\ln x}=\underbrace{ \lim\limits_{x\rightarrow \infty}\frac{1}{x^{-1}}}_{\text{L'Hôpital's Rule}}=\lim\limits_{x\rightarrow \infty}x=\infty \]
We conclude that \(x \ln x \ll x^{2}\) (Figure 4.50).
Question 4.19 L'Hôpital's Rule Progress Check 4
Calculate \(\displaystyle \lim \limits_{x \longrightarrow \infty} \frac{x^2}{e^x}\)
245
Example 10
Jonathan is interested in comparing two computer algorithms whose average run times are approximately \((\ln n)^{2}\) and \(\sqrt{n}\). Which algorithm takes less time for large values of \(n\)?
Solution Replace \(n\) by the continuous variable \(x\) and apply L’Hôpital’s Rule twice:
\[ \lim\limits_{x\rightarrow \infty}\frac{\sqrt{x}}{(\ln x)^2}=\underbrace{\lim\limits_{x\rightarrow \infty}\frac{\frac{1}{2}x^{-1/2}}{2x^{-1}\ln x}}_{\text{{L'Hôpital's Rule}}} = \underbrace{\lim\limits_{x\rightarrow \infty}\frac{x^{1/2}}{4\ln x}}_{\text{Simplify}} = \underbrace{\lim\limits_{x\rightarrow \infty}\frac{\frac{1}{2}x^{-1/2}}{4x^{-1}}}_{\text{L'Hôpital's Rule again}} = \underbrace{\lim\limits_{x\rightarrow \infty}\frac{x^{1/2}}{8}}_{\text{Simplify}} = \infty \]
This shows that \((\ln x)^2\ll\sqrt x\). We conclude that the algorithm whose average time is proportional to \((\ln n)^{2}\) takes less time for large \(n\).
In Section 1.6, we asserted that exponential functions increase more rapidly than the power functions. We now prove this by showing that \(x^{n} \ll e^{x}\) for every exponent n (Figure 4.51).
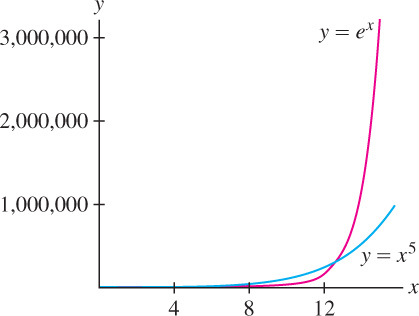
THEOREM 3 Growth of \(e^{x}\)
\[ \boxed{x^n\ll e^n\qquad\text{for every exponent }n} \]
In other words, \(\lim\limits_{x\rightarrow \infty}\frac{e^x}{x^n}=\infty\) for all \(n\).
Proof
The theorem is true for \(n = 0\) since \(\lim\limits_{x\rightarrow \infty}e^x = \infty\). We use L’Hôpital’s Rule repeatedly to prove that \(\frac{e^x}{x^n}\) tends to \(\infty \) for \(n = 1, 2, 3,\ldots\). For example,
\[ \lim\limits_{x\rightarrow \infty}\frac{e^x}{x} = \lim\limits_{x\rightarrow \infty}\frac{e^x}{1} = \lim\limits_{x\rightarrow \infty}e^x = \infty. \]
Then, having proved that \(\frac{e^x}{x} \rightarrow \infty\), we use L’Hôpital’s Rule again
\[ \lim\limits_{x\rightarrow \infty}\frac{e^x}{x^2} = \lim\limits_{x\rightarrow \infty}\frac{e^x}{2x} = \frac{1}{2} \lim\limits_{x\rightarrow \infty}\frac{e^x}{x} = \infty \]
Proceeding in this way, we prove the result for all whole numbers \(n\). A more formal proof would use the principle of induction. Finally, if \(k\) is any exponent, choose any whole number \(n\) such that \(n > k\). Then \(\frac{e^x}{x^n} < \frac{e^x}{x^k}\) for \(x > 1\), so \(\frac{e^x}{x^k}\) must also tend to infinity as \(x \rightarrow \infty\).
Question 4.20 L'Hôpital's Rule Progress Check 5
Calculate \(\displaystyle \lim \limits_{x \longrightarrow \infty} \frac{e^{4x}}{e^{3x}} \)
| A. |
| B. |
| C. |
| D. |
4.5.2 Proof of L’Hôpital’s Rule
A full proof of L’Hôpital’s Rule, without simplifying assumptions, is presented in a supplement on the text’s Companion Web Site.
We prove L’Hôpital’s Rule here only in the first case of Theorem 1—namely, in the case that \(f(a) = g(a) = 0\). We also assume that \(f'\) and \(g'\) are continuous at \(x = a\) and that \(g'(a) \neq 0\). Then \(g(x) \neq g(a)\) for \(x\) near but not equal to \(a\), and
\[ \frac{f(x)}{g(x)} = \frac{f(x) - f(a)}{g(x) - g(a)} = \frac{\dfrac{f(x)-f(a)}{x-a}}{\dfrac{g(x) - g(a)}{x-a}} \]
By the Quotient Law for Limits and the definition of the derivative,
\[ \lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)} = \frac{\lim\limits_{x\rightarrow a}\dfrac{f(x)-f(a)}{x-a}}{\lim\limits_{x\rightarrow a}\dfrac{g(x) - g(a)}{x-a}} = \frac{f'(a)}{g'(a)} = \lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)} \]
246
4.5.3 Section 4.5 Summary
- L’Hôpital’s Rule: Assume that \(f\) and \(g\) are differentiable near \(a\) and that
\[f(a) = g(a) = 0\]
Assume also that \(g'(x) \neq 0\) (except possibly at \(a\)). Then
\[ \lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)} = \lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)} \]
provided that the limit on the right exists or is infinite (\(\infty\) or \(-\infty\)).
- L’Hôpital’s Rule also applies to limits as \(x \rightarrow \infty\) or \(x \rightarrow -\infty\).
- Limits involving the indeterminate forms \(0^{0}\), \(1^{\infty }\), or \(\infty ^{0}\) can often be evaluated by first taking the logarithm and then applying L’Hôpital’s Rule.
- In comparing the growth rates of functions, we say that \(f(x)\) grows faster than \(g(x)\), and we write \(g \ll f\), if
\[ \lim\limits_{x\rightarrow \infty}\frac{f(x)}{g(x)}=\infty \]