4.8 Newton’s Method
 REMINDER A “zero” or “root” of a function f(x) is a solution of the equation f(x) = 0.
REMINDER A “zero” or “root” of a function f(x) is a solution of the equation f(x) = 0.
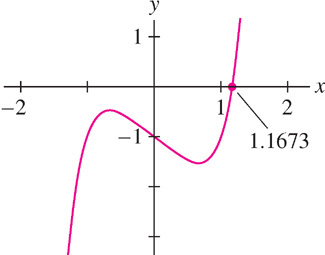
Newton’s Method is a procedure for finding numerical approximations to zeros of functions. Numerical approximations are important because it is often impossible to find the zeros exactly. For example, the polynomial \(f(x) = x^{5} - x - 1\) has one real root \(c\) (see Figure 4.76), but we can prove, using an advanced branch of mathematics called Galois Theory, that there is no algebraic formula for this root. Newton’s Method shows that \(c \approx 1.1673\), and with enough computation, we can compute \(c\) to any desired degree of accuracy.
In Newton’s Method, we begin by choosing a number \(x_{0}\), which we believe is close to a root of the equation \(f(x) = 0\). This starting value \(x_{0}\) is called the initial guess. Newton’s Method then produces a sequence \(x_{0}, x_{1}, x_{2},\ldots\) of successive approximations that, in favorable situations, converge to a root.
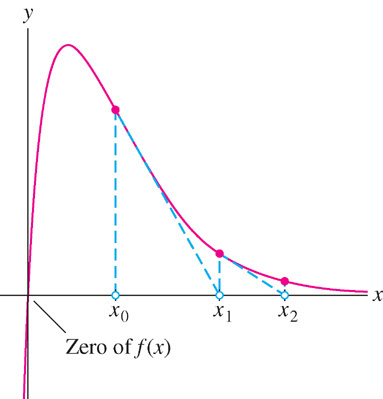
Figure 4.77 illustrates the procedure. Given an initial guess \(x_{0}\), we draw the tangent line to the graph at \((x_{0}, f(x_{0}))\). The approximation \(x_{1}\) is defined as the \(x\)-coordinate of the point where the tangent line intersects the \(x\)-axis. To produce the second approximation \(x_{2}\) (also called the second iterate), we apply this procedure to \(x_{1}\).
Let’s derive a formula for \(x_{1}\). The tangent line at \((x_{0}, f(x_{0}))\) has equation
\[y = f(x_{0}) + f'(x_{0})(x - x_{0})\]
The tangent line crosses the \(x\)-axis at \(x_{1}\), where
\[y = f(x_{0}) + f'(x_{0})(x_{1} - x_{0}) = 0\]
270
If \(f'(x_{0}) \neq 0\), we can solve for \(x_{1}\) to obtain \(x_{1} - x_{0} = - \frac{f(x_{0})}{f'(x_{0})}\), or
\[ x_{1} =x_0 - \frac{f(x_{0})}{f'(x_{0})} \]
The second iterate \(x_{2}\) is obtained by applying this formula to \(x_{1}\) instead of \(x_{0}\):
\[ x_{2} =x_1 - \frac{f(x_{1})}{f'(x_{1})} \]
and so on. Notice in Figure 4.77 that \(x_{1}\) is closer to the root than \(x_{0}\) and that \(x_{2}\) is closer still. This is typical: The successive approximations usually converge to the actual root. However, there are cases where Newton’s Method fails (see Figure 4.82 in Section 4.8.3).
Newton’s Method
Newton’s Method is an example of an iterative procedure. To “iterate” means to repeat, and in Newton’s Method we use Eq. (1) repeatedly to produce the sequence of approximations.
To approximate a root of \(f(x) = 0\):
Step 1. Choose initial guess \(x_{0}\) (close to the desired root if possible).
Step 2. Generate successive approximations \(x_{1}, x_{2},\ldots\), where
\[ x_{n+1} =x_n - \frac{f(x_{n})}{f'(x_{n})}\tag{1} \]
Example 1 Approximating \(\sqrt5\)
Calculate the first three approximations \(x_{1}, x_{2}, x_{3}\) to a root of \(f(x) = x^{2} - 5\) using the initial guess \(x_{0} = 2\).
Solution We have \(f'(x) = 2x\). Therefore,
\[ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}=x_0 - \frac{x_0^2-5}{2x_0}=\frac{x_0^2+5}{2x_0} \]
We compute the successive approximations as follows:
\begin{eqnarray*} x_1&=&x_0 - \frac{f(x_0)}{f'(x_0)}&=& 2 - \frac{2^2-5}{2\cdot2}&=&2.25\\ x_2&=&x_1 - \frac{f(x_1)}{f'(x_1)}&=& 2.25 - \frac{2.25^2-5}{2\cdot2.25}&\approx&2.23611\\ x_3&=&x_2 - \frac{f(x_2)}{f'(x_2)}&=& x_2 - \frac{x_2^2-5}{2\cdot x_2}&\approx& {\bf2.236067977}89 \end{eqnarray*}
This sequence provides successive approximations to a root of \(x^{2} - 5 = 0\), namely
\[ \sqrt5={\bf2.236067977}499789696\ldots \]
Observe that \(x_{3}\) is accurate to within an error of less than \(10^{-9}\). This is impressive accuracy for just three iterations of Newton’s Method.
4.8.1 Newton's Method and the Babylonians
We know that the Pythagorean Theorem relating the length of the legs of a right triangle to the length of its hypotenuse (\(a^2 + b^2 = c^2\)) was known to several civilizations, including the Babylonians. However, it was the early Greeks who were the first to give a proof.

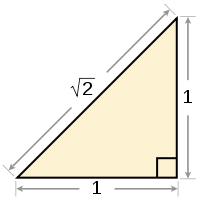
As a consequence of this theorem, for an isosceles right triangle with legs of unit length, the hypotenuse has length \(c = \sqrt{2}\). The Pythagorean Hipassus discovered that \(\sqrt{2}\) is not a fraction. For his brilliant insight, legend says that Hipassus was thrown overboard to drown in the Aegean Sea in order to keep this fact, which contradicted the teachings of Pythagoras himself, a secret.
For a video of a proof of this fact, click here (video to be created).
The fact that \(\sqrt{2}\) is not a fraction was almost certainly not known to the Babylonians. Nevertheless we know from clay tablets that they were ''very interested'' in \(\displaystyle \sqrt{2}\) and calculated its decimal value (in their sexagesimal system) to many places. By ''very interested'' we mean that they actually developed (for the very first time) an iteration scheme for the value of \(\sqrt{2}\).
They took an initial value \(x_0\), as a ''rough'' guess and then got a first approximation as \(\displaystyle x_1\):=\(\displaystyle \frac{x_0^2+2}{2x_0}\), and a second approximation \(\displaystyle x_2\) := \(\displaystyle \frac{x_1^2+2}{2x_1}\) and so on. As \(n\) gets larger, the \(n^{\text{th}}\) approximation \(x_{n}\) will get arbitrarily close to \(\sqrt{2}\).
Astoundingly, this, as we can see from Example 1 above, is Newton's Method for finding the zeros of \(f(x)=x^2-2\), i.e. \(\pm \sqrt{2}\). For example, if \(x_0=1\), then \(x_1=\frac{3}{2}\) and \(x_2 = \frac{17}{12}=1.416\ldots\), which is already accurate within two decimal places!
How did they discover this? Since they left no record of their thoughts, we simply do not know. It will have to remain a mystery!
4.8.2 How Many Iterations Are Required?
How many iterations of Newton’s Method are required to approximate a root to within a given accuracy? There is no definitive answer, but in practice, it is usually safe to assume that if \(x_{n}\) and \(x_{n+1}\) agree to \(m\) decimal places, then the approximation \(x_{n}\) is correct to these \(m\) places.
Example 2
 Let \(c\) be the smallest positive solution of \(\sin 3x = \cos x\).
Let \(c\) be the smallest positive solution of \(\sin 3x = \cos x\).
(a) Use a computer-generated graph to choose an initial guess \(x_{0}\) for \(c\).
(b) Use Newton’s Method to approximate \(c\) to within an error of at most \(10^{-6}\).
271
Solution
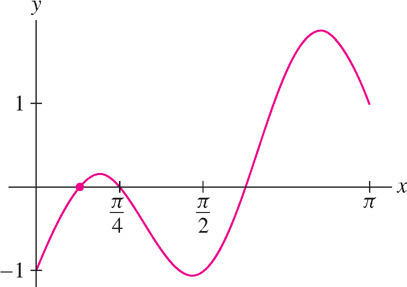
(a) A solution of \(\sin 3x = \cos x\) is a zero of the function \(f(x) = \sin 3x - \cos x\). Figure 4.81 shows that the smallest zero is approximately halfway between 0 and \(\frac{\pi}{4}\). Because \(\frac{\pi}{4}\approx0.785\), a good initial guess is \(x_{0} = 0.4\).
There is no single “correct” initial guess. In Example 2, we chose \(x_{0} = 0.4\), but another possible choice is \(x_{0} = 0\), leading to the sequence
\(\begin{align*} x_1&\approx 0.333 333 333 3\\ x_2&\approx 0.386 454 772 5\\ x_3&\approx 0.392 608 251 3\\ x_4&\approx 0.392 699 081 6 \end{align*}\)
You can check, however, that \(x_{0} = 1\) yields a sequence converging to \(x=\frac{\pi}{4}\), which is the second positive solution of \(\sin 3x =\cos x\).
(b) Since \(f'(x) = 3 \cos 3x + \sin x\), Eq. (1) yields the formula
\[ x_{n+1} = x_n - \frac{\sin3x_n - \cos x_n}{3\cos3x_n+\sin x_n} \]
With \(x_{0} = 0.4\) as the initial guess, the first four iterates are
\begin{align*} x_1&\approx 0.{\bf392}5647447 \\ x_2&\approx 0.{\bf392 699 0}382 \\ x_3&\approx 0.{\bf392 699 081 698 7}196 \\ x_4&\approx 0.{\bf392 699 081 698 7}214 \end{align*}
Stopping here, we can be fairly confident that \(x_{4}\) approximates the smallest positive root \(c\) to at least twelve places. In fact, \(c=\frac{\pi}{8}\) and \(x_{4}\) is accurate to sixteen places.
4.8.3 Which Root Does Newton’s Method Compute?
Sometimes, Newton’s Method computes no root at all. In Figure 4.82, the iterates diverge to infinity. In practice, however, Newton’s Method usually converges quickly, and if a particular choice of \(x_{0}\) does not lead to a root, the best strategy is to try a different initial guess, consulting a graph if possible. If \(f(x) = 0\) has more than one root, different initial guesses \(x_{0}\) may lead to different roots.
Example 3
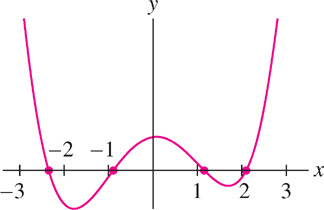
Figure 4.83 shows that \(f(x) = x^{4} - 6x^{2} + x + 5\) has four real roots.
(a) Show that with \(x_{0} = 0\), Newton’s Method converges to the root near \(-2\).
(b) Show that with \(x_{0} = -1\), Newton’s Method converges to the root near -1.
Solution We have \(f'(x) = 4x^{3} - 12x + 1\) and
\[ x_{n+1} = x_n - \frac{x_n^{4} - 6x_n^{2} + x_n + 5}{4x_n^{3} - 12x_n + 1} \]
(a) On the basis of Table 4.1, we can be confident that when \(x_{0} = 0\), Newton’s Method converges to a root near \(-2.3\). Notice in Figure 4.83 that this is not the closest root to \(x_{0}\).
(b) Table 4.2 suggests that with \(x_{0} = -1\), Newton’s Method converges to the root near \(-0.9\).
| \(x_{0}\) | \(0\) |
| \(x_{1}\) | \(-5\) |
| \(x_{2}\) | \(-3.9179954\) |
| \(x_{3}\) | \(-3.1669480\) |
| \(x_{4}\) | \(-2.6871270\) |
| \(x_{5}\) | \(-2.4363303\) |
| \(x_{6}\) | \(-2.3572979\) |
| \(x_{7}\) | \(-2.3495000\) |
| \(x_{0}\) | \(-1\) |
| \(x_{1}\) | \(-0.8888888888\) |
| \(x_{2}\) | \(-0.8882866140\) |
| \(x_{3}\) | \(-0.88828656234358\) |
| \(x_{4}\) | \(-0.888286562343575\) |
272
4.8.4 Section 4.8 Summary
- Newton’s Method: To find a sequence of numerical approximations to a root of \(f(x)\), begin with an initial guess \(x_{0}\). Then construct the sequence \(x_{0}, x_{1}, x_{2},\ldots\) using the formula
\[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \]
You should choose the initial guess \(x_{0}\) as close as possible to a root, possibly by referring to a graph. In favorable cases, the sequence converges rapidly to a root.
- If \(x_{n}\) and \(x_{n+1}\) agree to \(m\) decimal places, it is usually safe to assume that \(x_{n}\) agrees with a root to \(m\) decimal places.