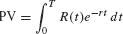THE INTEGRAL

5.8 Exponential Growth and Decay

In this section, we explore some applications of the exponential function. Consider a quantity P(t) that depends exponentially on time:

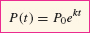
The constant k has units of “inverse time"; if t is measured in days, then k has units of (days)⁻¹.

If k > 0, then P(t) grows exponentially and k is called the growth constant. Note that P₀ is the initial size (the size at t = 0):

P (0) = P₀e^{[em]k[/em]·0} = P₀

We can also write P(t) = P₀b^t with b = e^k, because b^t = (e^k)^t = e^kt.

A quantity that decreases exponentially is said to have exponential decay. In this case, we write P(t) = P₀e^{−[em]kt[/em]} with k > 0; k is then called the decay constant.

Population is a typical example of a quantity that grows exponentially, at least under suitable conditions. To understand why, consider a cell colony with initial population P₀ = 100 and assume that each cell divides into two cells after 1 hour. Then population P(t) doubles with each passing hour:

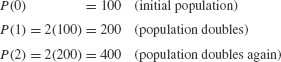
After t hours, P(t) = (100)2^t.

Exponential growth cannot continue over long periods of time. A colony starting with one E. coli cell would grow to 5 × 10⁸⁹ cells after 3 weeks—much more than the estimated number of atoms in the observable universe. In actual cell growth, the exponential phase is followed by a period in which growth slows and may decline.

EXAMPLE 1

In the laboratory, the number of Escherichia coli bacteria (Figure 1) grows exponentially with growth constant of k = 0.41 (hours)^-1. Assume that 1000 bacteria are present at time t = 0.

Figure 5.51: E. coli bacteria, found in the human intestine.

(a) Find the formula for the number of bacteria P(t) at time t.
(b) How large is the population after 5 hours?
(c) When will the population reach 10,000?

342

Solution The growth is exponential, so P(t) = P₀e^kt.

(a) The initial size is P₀ = 1000 and k = 0.41, so P(t) = 1000e^0.41t (t in hours).
(b) After 5 hours, P (5) = 1000e^0.41·5 = 1000e^2.05 ≈ 7767.9. Because the number of bacteria is a whole number, we round off the answer to 7768.
(c) The problem asks for the time t such that P(t) = 10,000, so we solve

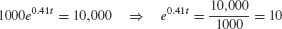
Taking the logarithm of both sides, we obtain ln(e^0.41t) = ln 10, or

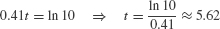
Therefore, P(t) reaches 10,000 after approximately 5 hours, 37 minutes (Figure 2).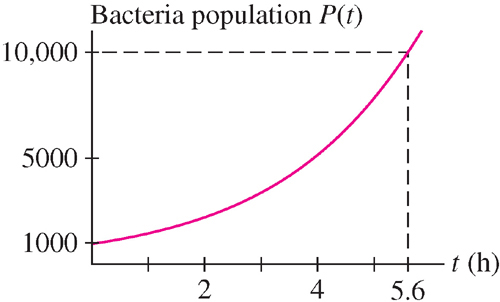

Figure 5.52: Growth of E. coli population.

The important role played by exponential functions is best understood in terms of the differential equation y′ = ky. The function y = P₀e^kt satisfies this differential equation, as we can check directly:

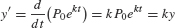
Theorem 1 goes further and asserts that the exponential functions are the only functions that satisfy this differential equation.

A differential equation is an equation relating a function y = f(x) to its derivative y′(or higher derivatives y′, y″, y‴,…).

THEOREM 1

If y(t) is a differentiable function satisfying the differential equation

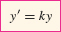
then y(t) = P₀e^kt, where P₀ is the initial value P₀ = y(0).

Proof

Compute the derivative of ye^{−[em]kt[/em]}. If y′ = ky, then

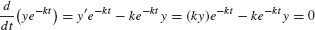
Because the derivative is zero, y(t)e^{−[em]kt[/em]} = P₀ for some constant P₀, and y(t) = P₀e^kt as claimed. The initial value is y (0) = 0 = P₀e⁰ = P₀.

CONCEPTUAL INSIGHT

Theorem 1 tells us that a process obeys an exponential law precisely when its rate of change is proportional to the amount present. This helps us understand why certain quantities grow or decay exponentially.

A population grows exponentially because each organism contributes to growth through reproduction, and thus the growth rate is proportional to the population size. However, this is true only under certain conditions. If the organisms interact—say, by competing for food or mates—then the growth rate may not be proportional to population size and we cannot expect exponential growth.

Similarly, experiments show that radioactive substances decay exponentially. This suggests that radioactive decay is a random process in which a fixed fraction of atoms, randomly chosen, decays per unit time (Figure 3). If exponential decay were not observed, we might suspect that the decay was influenced by some interaction between the atoms.

Figure 5.53: Computer simulation of radioactive decay as a random process. The red squares are atoms that have not yet decayed. A fixed fraction of red squares turns white in each unit of time.

343

EXAMPLE 2

Find all solutions of y′ = 3y. Which solution satisfies y (0) = 9?

Solution The solutions to y′ = 3y are the functions y(t) = Ce^3[em]t[/em], where C is the initial value C = y (0). The particular solution satisfying y (0) = 9 is y(t) = 9e^3[em]t[/em].

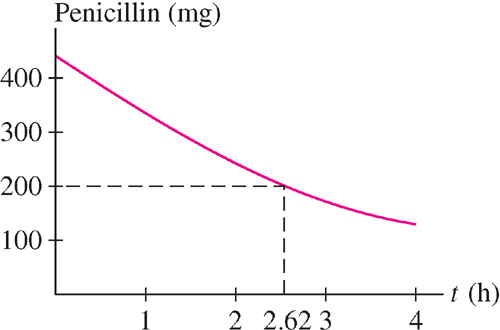
EXAMPLE 3 Modeling Penicillin

Pharmacologists have shown that penicillin leaves a person’s bloodstream at a rate proportional to the amount present.

(a) Express this statement as a differential equation.
(b) Find the decay constant if 50 mg of penicillin remains in the bloodstream 7 hours after an initial injection of 450 mg.
(c) Under the hypothesis of (b), at what time was 200 mg of penicillin present?

Solution

(a) Let A(t) be the quantity of penicillin present in the bloodstream at time t. Since the rate at which penicillin leaves the bloodstream is proportional to A(t),

where k > 0 because A(t) is decreasing.
(b) Eq. (1) and the condition A (0) = 450 tell us that A(t) = 450e^{−[em]kt[/em]}. The additional condition A (7) = 50 enables us to solve for k:
Thus, .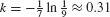
(c) To find the time t at which 200 mg was present, we solve

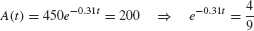
Therefore,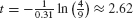 hours (Figure 4).

Figure 5.54: The quantity of penicillin in the bloodstream decays exponentially.

The constant k has units of time⁻¹, so the doubling time T = (ln 2)/k has units of time, as we should expect. A similar calculation shows that the tripling time is (ln 3)/k, the quadrupling time is (ln 4)/k, and, in general, the time to n-fold increase is (ln n)/k.

Quantities that grow exponentially possess an important property: There is a doubling time T such that P(t) doubles in size over every time interval of length T. To prove this, let P(t) = P₀e^kt and solve for T in the equation P(t + T) = 2P(t).

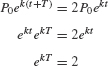
We obtain kT = ln 2 or T = (ln 2)/k.

Doubling Time

If P(t) = P₀e^kt with k > 0, then the doubling time of P is

EXAMPLE 4 Spread of the Sapphire Worm

A computer virus nicknamed the Sapphire Worm spread throughout the Internet on January 25, 2003 (Figure 5). Studies suggest that during the first few minutes, the population of infected computer hosts increased exponentially with growth constant k = 0.0815 s⁻¹.

Figure 5.55: Spread of the Sapphire computer virus 30 minutes after release. The infected hosts spewed billions of copies of the virus into cyberspace, significantly slowing Internet traffic and interfering with businesses, flight schedules, and automated teller machines.

344

(a) What was the doubling time of the virus?
(b) If the virus began in four computers, how many hosts were infected after 2 minutes? After 3 minutes?

Solution

(a) The doubling time is (ln 2)/0.0815 ≈ 8.5 seconds (Figure 6).

Figure 5.56: Doubling (from 4 to 8 to 16, etc.) occurs at equal time intervals.
(b) If 4, the number of infected hosts after t seconds is P(t) = 4e^0.0815t. After 2 minutes (120 seconds), the number of infected hosts is
P (120) = 4e^0.0815(120) ≈ 70,700
After 3 minutes, the number would have been P (180) = 4e^0.0815(180) ≈ 9.4 million. However, it is estimated that a total of around 75,000 hosts were infected, so the exponential phase of the virus could not have lasted much more than 2 minutes.

In the situation of exponential decay P(t) = P₀e^{−[em]kt[/em]}, the half-life is the time it takes for the quantity to decrease by a factor of 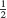. The calculation similar to that of doubling time above shows that

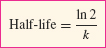
EXAMPLE 5

The isotope radon-222 decays exponentially with a half-life of 3.825 days. How long will it take for 80% of the isotope to decay?

Solution By the equation for half-life, k equals ln 2 divided by half-life:

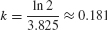
Therefore, the quantity of radon-222 at time t is R(t) = R₀e^{−0.181[em]t[/em]}, where R₀ is the amount present at t = 0 (Figure 7). When 80% has decayed, 20% remains, so we solve for t in the equation R₀e^{−0.181[em]t[/em]} = 0.2R₀:

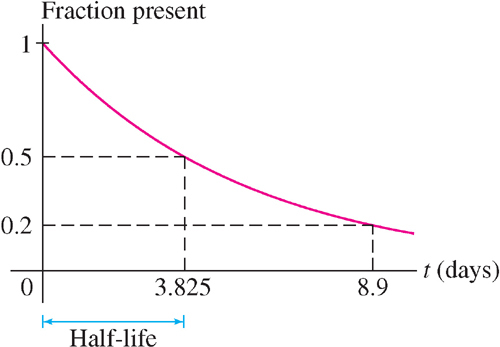
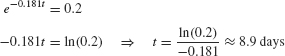
Figure 5.57: Fraction of radon-222 present at time t.

The quantity of radon-222 decreases by 80% after 8.9 days.

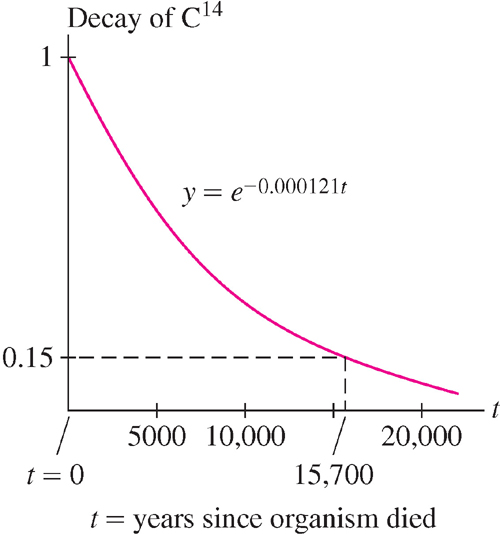
Carbon Dating

Carbon dating (Figure 8) relies on the fact that all living organisms contain carbon that enters the food chain through the carbon dioxide absorbed by plants from the atmosphere. Carbon in the atmosphere is made up of nonradioactive C¹² and a minute amount of radioactive C¹⁴ that decays into nitrogen. The ratio of C¹⁴ to C¹² is approximately R_atm = 10⁻¹².

Figure 5.58: American chemist Willard Libby (1908–1980) developed the technique of carbon dating in 1946 to determine the age of fossils and was awarded the Nobel Prize in Chemistry for this work in 1960. Since then the technique has been refined considerably.

The carbon in a living organism has the same ratio R_atm because this carbon originates in the atmosphere, but when the organism dies, its carbon is no longer replenished. The C¹⁴ begins to decay exponentially while the C¹² remains unchanged. Therefore, the ratio of C¹⁴ to C¹² in the organism decreases exponentially. By measuring this ratio, we can determine when the death occurred. The decay constant for C¹⁴ is k = 0.000121 yr⁻¹, so

Ratio of C¹⁴ to C¹² after t years = R_atme^{−0.000121[em]t[/em]}

345

EXAMPLE 6 Cave Paintings

In 1940, a remarkable gallery of prehistoric animal paintings was discovered in the Lascaux cave in Dordogne, France (Figure 9). A charcoal sample from the cave walls had a C¹⁴-to-C¹² ratio equal to 15% of that found in the atmosphere. Approximately how old are the paintings?

Figure 5.59: Detail of bison and other animals from a replica of the Lascaux cave mural.

Solution The C¹⁴-to-C¹² ratio in the charcoal is now equal to 0.15R_atm, so

R_atme^{−0.000121[em]t[/em]} = 0.15 R_atm

where t is the age of the paintings. We solve for t:

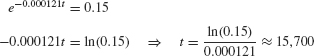
The cave paintings are approximately 16,000 years old (Figure 10).

Figure 5.60: If only 15% of the C¹⁴ remains, the object is approximately 16,000 years old.

Compound Interest and Present Value

Exponential functions are used extensively in financial calculations. Two basic applications are compound interest and present value.

Convention: Time t is measured in years and interest rates are given as yearly rates, either as a decimal or as a percentage. Thus, r = 0.05 corresponds to an interest rate of 5% per year.

When a sum of money P₀, called the principal, is deposited into an interest-bearing account, the amount or balance in the account at time t depends on two factors: the interest rate r and frequency with which interest is compounded. Interest paid out once a year at the end of the year is said to be compounded annually. The balance increases by the factor (1 + r) after each year, leading to exponential growth:

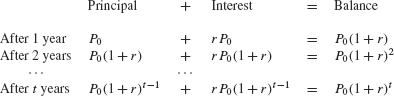
346

Suppose that interest is paid out quarterly (every 3 months). Then the interest earned after 3 months is 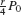dollars and the balance increases by the factor 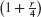. After one year (4 quarters), the balance increases to 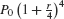and after t years,

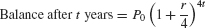
For example, if P₀ = 100 and r = 0.09, then the balance after one year is

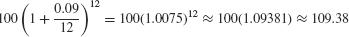
More generally,

Compound Interest

If P₀ dollars are deposited into an account earning interest at an annual rate r, compounded M times yearly, then the value of the account after t years is

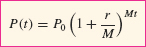
The factor 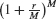is called the yearly multiplier.

Table 1 shows the effect of more frequent compounding. What happens in the limit as M tends to infinity? This question is answered by the next theorem (a proof is given at the end of this section).

Table : Compound Interest with Principal P₀ = $100 and r = 0.09

THEOREM 2

Limit Formula for e and e^x

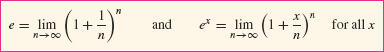
Figure 11 illustrates the first limit graphically. To compute the limit of the yearly multiplier as M → ∞, we apply the second limit with x = r and n = M:

Figure 5.61: The function

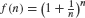approaches e as n → ∞.

The multiplier after t years is (e^r)^t = e^rt. This leads to the following definition.

Continuously Compounded Interest

If P₀ dollars are deposited into an account earning interest at an annual rate r, compounded continuously, then the value of the account after t years is

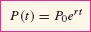
EXAMPLE 7

A principal of 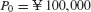(Japanese yen) is deposited into an account paying 6% interest. Find the balance after 3 years if interest is compounded quarterly and if interest is compounded continuously.

347

Solution After 3 years, the balance is

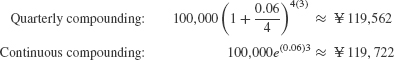
Note: The mathematics of interest rates is the same for all currencies (dollars, euros, pesos, yen, etc.).

Present Value

The concept of present value (PV) is used in business and finance to compare payments made at different times. Assume that there is an interest rate r (continuously compounded) at which an investor can lend or borrow money. By definition, the PV of P dollars to be received t years in the future is Pe^{−[em]rt[/em]}:

In the financial world there are many different interest rates (federal funds rate, prime rate, LIBOR, etc.). We simplify the discussion by assuming that there is just one rate.

What is the reasoning behind this definition? When you invest at the rate r for t years, your principal increases by the factor e^rt, so if you invest Pe^{−[em]rt[/em]} dollars, your principal grows to (Pe^{−[em]rt[/em]})e^rt = P dollars at time t. The present value Pe^{−[em]rt[/em]} is the amount you would have to invest today in order to have P dollars at time t.

EXAMPLE 8

Is it better to receive $2000 today or $2200 in 2 years? Consider r = 0.03 and r = 0.07.

Solution We compare $2000 today with the PV of $2200 received in 2 years.

If r = 0.03, the PV is 2200e^−(0.03)2 ≈ $2071.88. This is more than $2000, so a payment of $2200 in 2 years is preferable to a $2000 payment today.
If r = 0.07, the PV is 2200e^−(0.07)2 ≈ $1912.59. This PV is less than $2000, so it is better to receive $2000 today if r = 0.07.

EXAMPLE 9 Deciding Whether to Invest

Chief Operating Officer Ryan Martinez must decide whether to upgrade his company’s computer system. The upgrade costs $400,000 and will save $150,000 a year for each of the next 3 years. Is this a good investment if r = 7%?

Solution Ryan must compare today’s cost of the upgrade with the PV of the money saved. For simplicity, assume that the annual savings of $150,000 is received as a lump sum at the end of each year.

If r = 0.07, the PV of the savings over 3 years is

150,000e^−(0.07) + 150,000e^−(0.07)2 + 150,000e^−(0.07)3 ≈ $391,850

The amount saved is less than the cost $400,000, so the upgrade is not worthwhile.

An income stream is a sequence of periodic payments that continue over an interval of T years. Consider an investment that produces income at a rate of $800/year for 5 years. A total of $4000 is paid out over 5 years, but the PV of the income stream is less. For instance, if r = 0.06 and payments are made at the end of the year, then the PV is

800e^−0.06 + 800e^−(0.06)2 + 800e^−(0.06)3 + 800e^−(0.06)4 + 800e^−(0.06)5 ≈ $3353.12

348

It is more convenient mathematically to assume that payments are made continuously at a rate of R(t) dollars per year. We can then calculate PV as an integral. Divide the time interval [0, T] into N subintervals of length Δt = T/N. If Δt is small, the amount paid out between time t and t + Δt is approximately

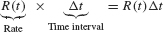
The PV of this payment is approximately e^{−[em]rt[/em]} R(t)Δt. Setting t_i = iΔt, we obtain the approximation

This is a Riemann sum whose value approaches .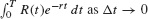

In April 1720, Isaac Newton doubled his money by investing in the South Sea Company, an English company set up to conduct trade with the West Indies and South America. Having gained 7000 pounds, Newton invested a second time, but like many others, he did not realize that the company was built on fraud and manipulation. In what became known as the South Sea Bubble, the stock lost 80% of its value, and the famous scientist suffered a loss of 20,000 pounds.

PV of an Income Stream

If the interest rate is r, the present value of an income stream paying out R(t) dollars per year continuously for T years is

EXAMPLE 10

An investment pays out 800,000 Mexican pesos per year, continuously for 5 years. Find the PV of the investment for r = 0.04 and r = 0.06.

Solution In this case, R(t) = 800,000. If r = 0.04, the PV of the income stream is equal (in pesos) to

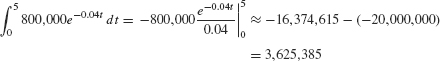
If r = 0.06, the PV is equal (in pesos) to

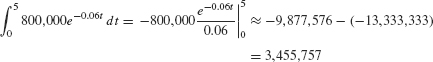
Proof of Theorem 2

Apply the formula 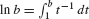with b = 1 + 1/n:

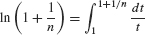
Figure 12 shows that the area represented by this integral lies between the areas of two rectangles of heights n/(n + 1) and 1, both of base 1/n. These rectangles have areas 1/(n + 1) and 1/n, so

Figure 5.62

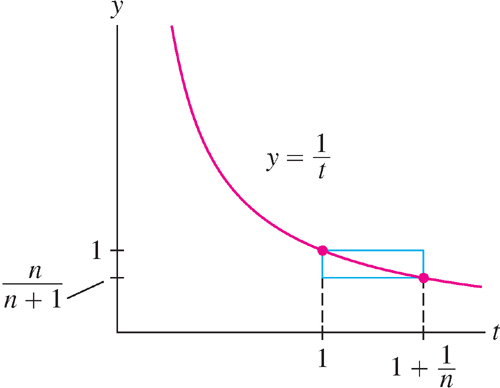
349

Multiply through by n, using the rule n ln a = ln aⁿ:

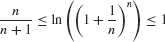
Since , the middle quantity must approach 1 by the Squeeze Theorem:

Now we can apply e^x (because it is continuous) to obtain the desired result:

See Exercise 61 for a proof of the more general formula .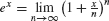

5.8.1 Summary

Exponential growth with growth constant k > 0: P(t) = P₀e^kt.
Exponential decay with decay constant k > 0: P(t) = P₀e^e−kt.
The solutions of the differential equation y′ = ky are the exponential functions y = Ce^kt, where C is a constant.
A quantity P(t) grows exponentially if it grows at a rate proportional to its size—that is, if P′ (t) = kP(t).
The doubling time for exponential growth and the half-life for exponential decay are both equal to (ln 2)/k.
For use in carbon dating: the decay constant of C¹⁴ is k = 0.000121.
Interest rate r, compounded M times per year:
P(t) = P₀(1 + r/M)^Mt
Interest rate r, compounded continuously: P(t) = P₀e^rt.
The present value (PV) of P dollars (or other currency), to be paid t years in the future, is Pe^{−[em]rt[/em]}.
Present value of an income stream paying R(t) dollars per year continuously for T years: